◆愛知県 Y.M.Ojisan さんからの解答。

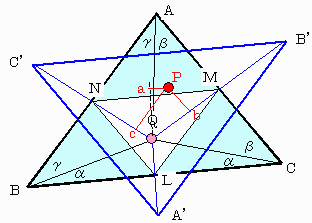
Pが△ABCの外心:Qであるとき、Pから各辺への推薦の足をL,M,Nとすると、
| △LMNの面積は | S 4 |
である。 |
一方相似比から S’=4△LMNであるから、この時S=S’である。
一般のPの位置をQからのずれ(a,b,c)で表すこととする。
ここでa,b,cは
a=QP・eQL ,b=QP・eQM 、c=QP・eQN
で定義され eQXは QX方向の単位ベクトルである。
また、角度αβγを上図のように定義する。
| αβγは条件より | π 2 |
未満の正の数である。 |
| またα+β+γ= | π 2 |
---(1)である。 |
一般性を失わず△ABCの外接円の半径を1とする。
即ちQA=QB=QC=1。
この時 BC=2cosα>0,CA=2cosβ>0,AB=2cosγ>0
a,b,cには線形の条件があって、面積S一定より
S= (sinα-a)*cosα+ (sinβ-b)*cosβ+ (sinγ-c)*cosγ
=sinα*cosα+sinβ*cosβ+sinγ*cosγ
すなわち a*cosα+b*cosβ+ c*cosγ=0 --(2)
一方 sin(β+γ)=cosα およびその輪換の関係を用いると
S'/2 =(sinβ-b)*(sinγ-c)*cosα+(sinα-a)*(sinγ-c)*cosβ+(sinβ-b)*(sinα-a)*cosγ =b*c*cosα+a*c*cosβ+ b*a*cosγ-b*(sinγ*cosα+ sinα*cosγ) -c*(sinβ*cosα+ sinα*cosβ) -a*(sinγ*cosβ+ sinβ*cosγ)+sinβ*sinγ*cosα+sinα*sinγ*cosβ+sinβ*sinα*cosγ =b*c*cosα+a*c*cosβ+b*a*cosγ-(a*cosα+b*cosβ+ c*cosγ)+(sinα*cosα+sinβ*cosβ+sinγ*cosγ)/2 =b*c*cosα+a*c*cosβ+ b*a*cosγ + S/2 ---(3)よって、(1)(2)条件下で(3)の最大値を求めればよい。
cosα(S'-S)/2
= b*c*cos2α-(c*cosβ+ b*cosγ)(b*cosβ+ c*cosγ)
=b*c*(cos2α- cos2γ- cos2β)- cosγ*cosβ*(b2+c2)
cos2α- cos2γ- cos2β
=(sin2β-1)*cos2γ+( sin2γ-1)*cos2β+2 sinβcosγsinγcosβ
=2cosβcosγ(sinβsinγ-cosβcosγ)
=−2cosβcosγsinα
cosα(S-S')/4cosβcosγ
=(b2+2*b*c*sinα+c2)
=(|b|-|c|)2+2(1-sinα)*|b*c|≧0
等号はb=c=0 同様に a=0 。
よって、cosα>0 cosβ>0 cosγ>0であるから S≧S'
等号はa=b=c=0、即ち外心のとき。
◆出題者のコメント。
Y.M.Ojisanさん、解答ありがとうございます。
外心から各辺に下した垂線上の点でPの位置を表す、という方法は考え付きませんでした。
Y.M.Ojisanさんの証明のようにPの位置や角度を定めると、SとS'の関係がきれいに表されますね。
見事正解です。
私は次のような方法で証明しました。
△ABCの外接円の半径をR、外心をOとし、Pから辺BC、CA、ABに下ろした垂線の足をそれぞれD、E、Fとする。
また、辺BC、CA、ABの長さをそれぞれa、b、cとする。
| Oを起点とするOB方向の単位ベクトルを | → OB |
、同様に | → OC |
とする。 |
点Pが△OBCの周上または内部にある場合、
0≦r≦R、0≦t≦1である実数r、tを用いて
| → OP | = r*{(1-t)* | → OB |
+ t* | → OC |
} |
PD = (R-r)cosA
| PE = (R-r)cosB + | ra R |
sinC*(1-t) |
| PF = (R-r)cosC + | ra R |
sinB*t |
と表され、この式を
| S' 4 |
= | 1 2 |
*PD*PE*sinC + | 1 2 |
*PE*PF*sinA + | 1 2 |
*PF*PD*sinB ・・・(1) |
に代入し、正弦定理を用いてsinを消去すると、
(1)の第2項
| = | a 2R |
*{- | r2*a2*bc 4*R4 | *t2 +[ | r2*a2*bc 4*R4 |
+ | ra*(R-r)*(bcosB-ccosC) 2*R2 |
]*t+(R-r)cosC*[(R-r)cosB+ | rac 2*R2 |
]} |
(1)の第1項 + 第3項
| = (R-r)cosA*{ | ra(b2-c2) 4*R3 |
*t+(R-r)* | a 2R | + | ra*c2 4*R3 | } |
| S' = | abc 16*R3 |
*{(R+r)(R-r) -( | ra R | ) | 2 | *t(1-t)} |
| を得る。ここで、S = | abc 4R |
より、 |
S-S' ≧ 0
| ⇔ | abc 4*R5 |
*[(Rr)2 - t*(1-t)*(ra)2] ≧ 0 |
| 右辺は t = | 1 2 |
の時に最大となるので |
よってPが△OBCの周上または内部にある場合S≧S'であり、対称性より△OCA、△OABでも良い。
| またSの式にt= | 1 2 |
を代入してrについての式と見ると、 |