『(2ⁿ-1)！の性質』解答

◆北海道　キューダ さんからの解答。

問題文が間違えていなければ、証明不能です。
反例として、n=7,8,9,...　等があるからです。

具体的に、Mod[f((2ⁿ-1)!),2ⁿ⁺¹]は、次のような値を取ります。

1,3,11,11,11,11,139,139,651,1675,1675,5771,5771,5771,5771,71307,...

ちなみに、(2ⁿ-1)!には、(2ⁿ-n-1)個、２の因子があるので、

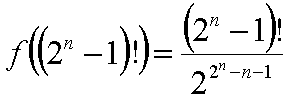
となります。

◆愛知県　Y.M.Ojisan さんからの解答。

n=7 以降正しくないようです。
ただし　139=128+11 651=512+139 1675=1024+651...　　
なので　mod 128 固定ならＯＫ

 n f((2n-1)!) mod 2n+1    11 mod 2n+1  2n-1       2n+1
 1         1                   3         1         4 
 2         3                   3         3         8 
 3        11                  11         7        16 
 4        11                  11        15        32 
 5        11                  11        31        64 
 6        11                  11        63       128 
 7       139                  11       127       256 
 8       139                  11       255       512 
 9       651                  11       511      1024 
10      1675                  11      1023      2048 
11      1675                  11      2047      4096 
12      5771                  11      4095      8192 
13      5771                  11      8191     16384 
14      5771                  11     16383     32768 
15      5771                  11     32767     65536 
16     71307                  11     65535    131072 
17     71307                  11    131071    262144 
18    333451                  11    262143    524288 
19    857739                  11    524287   1048576 
20   1906315                  11   1048575   2097152 

以上

確認ソフト

PRINT "n  f((2^n-1)!)mod2^(n+1)  11mod2^(n+1)  2^n-1  2^(n+1)"
FOR n=1 TO 20
   LET  mm=2^(n+1)
   LET  NN=2^n-1
   LET  K=1
   FOR i=1 TO NN
      LET  J=i
      DO WHILE MOD(J,2)=0
         LET  J=J/2
      LOOP
      LET  K=MOD(K*J,mm)
   NEXT i
   PRINT USING"##   #######             #######   #######   ####### ": n,K,MOD(11,mm),NN,mm
NEXT n
END

◆沖縄県　jpgr さんからの解答。

【問題２】

帰納法で示す。

n＝3のとき、
　　(2ⁿ−1)!!＝(2³−1)!!＝105≡1　(mod 2³)
で、成り立つ。

n＝k≧3の時も成り立つとする。つまり、

　　(2^k−1)!!≡1　(mod 2^k)

とする。

ここで、

　　(2^k−1)!!＝(2^k)×Q(k)＋1

と置く。Q(k)は自然数である。

n＝k＋1のとき、

　{2^k+1−1}!!
＝{2^k+1−1}×{2^k+1−3}×...×(2^k＋1)×(2^k−1)!!
≡(−1)×(−3)×...×{−(2^k−1)}×(2^k−1)!!　---(1)

ここで、(−1)から{−(2^k−1)}までの項数は2^k-1、
つまり偶数個であるから、(1)は、

　(−1)^{2k-1}×{1×3×...×(2^k−1)}×(2^k−1)!!
＝{(2^k−1)!!}²
＝{2^k×Q(k)＋1}²
＝2^2k×{Q(k)}²＋2^k+1×Q(k)＋1
≡1　(mod 2^k+1)

以上より題意は示せた。

　『(2ⁿ-1)！の性質』へ

　数学の部屋へもどる