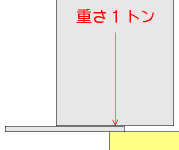
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俀偮偺堦墌嬍偺丄偢傜偟偨曽岦偺抂偐傜抂傑偱偺挿偝(們倣乯偼
柧傜偐偵丄俀亄俙丅
傛偭偰丄廳怱埵抲(們倣)偼丄偦偺椉抂偐傜 侾亄侽.俆俙
亂栤戣俀亃
亂栤戣侾亃偺寢壥偲丄侽亙俙亙侾傛傝丄偼傒偩偟壜擻偺挿偝(們倣)亙侾.俆
偮傑傝丄侾.俆們倣(堦墌嬍偺捈宎偺俁/係)枹枮側傜丄尷傝側偔偦傟偵嬤偯偗偰偼傒偩偣傞丅
亂栤戣俁亃
壗偙廳偹傛偆偲丄婘傗奺堦墌嬍偵偲偭偰傒傟偽丄帺暘傛傝忋偵偁傞堦墌嬍慡懱偺廳怱偼丄帺暘偐傜偼傒偩偣側偄丅
乮偼傒偩偡偲丄忋偵偁傞堦墌嬍慡懱偑帺暘(婘傗奺堦墌嬍)偐傜棊偪偰偟傑偆丅乯
偲偙傠偑丄偦偆側傜側偄斖埻側傜丄堦墌嬍偺悢傪尷傝側偔憹傗偡偙偲偱丄偄偔傜偱傕慡懱偺廳怱埵抲傪侾斣壓偺堦墌嬍偺抂偵嬤偯偗傜傟傞丅
傛偭偰丄侾斣壓偺堦墌嬍偼傎傫偺嬐偐偱傕柺(揰偱偼側偄)偑婘偵愙偟偰偄傟偽棟榑揑偵偼壜擻丅
偮傑傝丄俀們倣枹枮側傜丄尷傝側偔偦傟偵嬤偯偗偰偼傒偩偣傞丅

亂俹丒俽亃
堦墌嬍偺捈宎偼栺俀噋偱偡偑丄懡偔偺恖偑丄乽捈宎俀噋偺墌傪昤偗乿偲尵偆偲傎傏惓妋偵彂偗傞偺偵丄乽堦墌嬍傪昤偗乿偲尵偆偲丄幚嵺傛傝彫偝偔昤偄偰偟傑偆偦偆偱偡丅
乽偦傟偼堦墌嬍傪攏幁偵偟偰偄傞偐傜偩乿偲偄偆愢傑偱偁傞偲偐乧丅
傑偨丄堦墌嬍偺廳偝偼傄偭偨傝侾倗丄偄偔偮傕偁傟偽暘摵戙傢傝偵傕巊偊傑偡丅
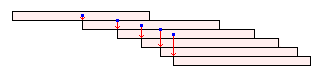
仧垽抦導丂juin 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俀偮偺堦墌嬍偺廳怱傪寢傫偩慄暘偺拞揰丅
亂栤戣俀亃
侾偮傔偺堦墌嬍偺廳怱偺恀壓偵俀枃栚偺堦墌嬍偺抂偑偔傞傛偆偵偡傞丅
嫟捠廳怱偼俀枃偺廳怱偺拞揰偵偁傞偐傜丄
侾亄侽丏俆亖侾丏俆
婘偐傜侾丏俆們倣偼傒偩偡偙偲偑偱偒傞丅
亂栤戣俁亃
婔傜偱傕偼傒偩偟偰偺偣傞偙偲偑偱偒傞丅
棟桼
侾枃栚偺堦墌嬍偺嵍抂傪侽丄拞怱傪G1(1)偲偟偰嵗昗傪擖傟傞丅
婘偺嵍抂傪侾偵偁傢偣傟偽堦墌嬍傪偺偣傞偙偲偑偱偒傞丅
俀枃栚偺堦墌嬍偺嵍抂傪侾丄拞怱傪C2(2)偵偁傢偣傞丅
廳怱G2偼侾亄侾乛俀亖俁乛俀
婘偺嵍抂傪G2(3/2)偵偁傢偣傟偽掁傝偁偆丅
俁枃栚偺堦墌嬍偺嵍抂傪俁乛俀丄拞怱C3傪俁乛俀亄侾偵偁傢偣傞丅
廳怱G3偼慄暘G2C3傪2:1偵撪暘偡傞丅
C2G3=1偩偐傜丄G3偼1+1/2+1/3丅
偙偙偵婘偺嵍抂傪偁傢偣傞丅
寢嬊n枃偺侾墌嬍傪廳偹偨帪丄廳怱Gn偼1+1/2+...+1/n偵偁傞丅
Gn偵丄婘偺嵍抂傪偁傢偣傟偽椙偄丅
仧嶳棞導丂Footmark 偝傫偐傜偺僐儊儞僩丅
側傞傎偳丄妋偐偵juin偝傫偺偍偭偟傖傞偲偍傝丄偄偔傜偱傕偼傒偩偣傑偡偹丅乮丱丱丟
偳傟傕丄偦傟傛傝忋偵偁傞堦墌嬍慡懱偺廳怱埵抲偵丄偡偖壓偺堦墌嬍(嵟屻偵婘)偺嵍抂傪崌傢偣傞偺偱丄巹偺帵偟偨忦審傕慛傗偐偵僋儕傾偟偰偄傞忋偵丄偼傒偩偟傕忢偵嵟戝偲側傝傑偡偹丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣俁亃
悢妛揑偵偼juin偝傫偺摎偊偱傛偄傢偗偱偡偑丄尰幚偵偼偳偆側傫偱偟傚偆偐丅
偲偼偄偊姰帏側尰幚傪専摙偡傞偺偼柍棟側偺偱丄偙偙偱偼
乮侾乯堦條廳椡応倗亖俋丏俉m/s
乮俀乯晽偲偐怳摦摍偼側偄
乮俁乯婘偼悈暯偱傊偙傑側偄
乮係乯堦墌嬍偼姰帏側嬒幙墌斦
丂敿宎倰亖侽丏侽侾倣丄岤傒倛亖侽丏侽侽侾俀倣丄幙検m=侽丏侽侽侾kg
乮俆乯傾儖儈偺婡夿揑摿惈偲偟偰
丂冃y亖俁侽侽俵俹倎丄俤亖俉侽俧俹倎丄兪亖侽丏侾俆偲偟傑偡丅
偙偙偱冃y偼崀暁乮偮傇傟傞乯墳椡偱峲嬻婡梡偺摿偵嫮偄傕偺偺掱搙偲偟傑偟偨丅
俤偼儎儞僌棪乮僶僱掕悢乯丄兪偼惷巭杸嶤學悢偱偡丅
墌斦偺崅偝偼栤戣愝掕傛傝傕偆彮偟惛搙傪忋偘偰侾丏俀倣倣偲偟傑偡丅
亂偮傇傟側偄亃
偁傑傝崅偔愊傓偲丄壓偺曽偼廳傒偵懴偊偐偹偰捵傟傑偡丅
偦偺尷奅偺侾墌嬍忋偺廳偝偼丂兾倰2冃y偱偡丅
堦曽値枃偺侾墌嬍偺廳偝偼値倗倣偱偡丅
傛偭偰丂値亖兾倰2冃y乛倗倣丄慡懱偺崅偝俫亖値倛
| 挘傝偩偟検 倃(n)= | n 儼 i=1 |
[ | 倰 倝 |
]佮倰{ln(値亄侽丏俆)亄侽丏俆俈俈俀侾俋俈俋} |
偱偡丅
寁嶼偡傞偲丂値亖俋俇侾俈侾俀侽丄俫亖侾侾丏俆係倠倣丄倃亖侽丏侾俇俇俆俇倣
偡側傢偪栺侾俈們倣偱偡丅
懳棳寳傪挻偊偰傗偭偲侾俈們倣側偺偱偡偹丅
側偍崅偝偺弅傒検乮栺侽丏俀亾乯偼柍帇偟傑偟偨丅
亂偍偪側偄亃
嵟傕栤戣側偺偼傾儖儈偑寢峔廮傜偐偄偙偲偱偡丅
乮峲嬻婡偵忔偭偰棎婥棳偵弌偔傢偡偲僄儞僕儞億僢僪傗庡梼偑僌儔僌儔梙傟偰偄傑偡傛偹丅>,<"乯
丂傑偭偡偖偵愊傒忋偘傟偽慜婰偺擛偔偱偡偑丄偙偺栤戣偺傛偆偵偢傜偟偰愊傓偲丄儌乕儊儞僩偑摥偄偰偳傫偳傫孹偄偰備偒丄偮偄偵偼妸傝棊偪偰偟傑偄傑偡丅
偦偺孹偒偼兪偱偁偭偰丄侽丏侾俆偺偲偒栺俉丏俆搙偱偡丅
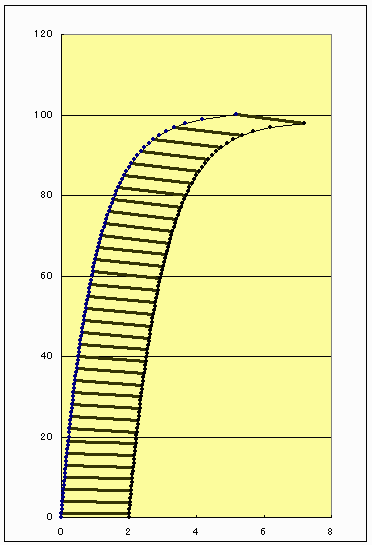
壓恾柾幃恾乮n=100傪屩挘乯嶲徠
忋偐傜値枃傪値亄侾枃栚偵抲偄偨偲偒偺値亄侾枃栚偺拞怱傪巟揰偲偡傞儌乕儊儞僩俵値偼
丂俵値亖倗倣値*(倰乛値)亄俵値亅侾亖倰倗倣値亖倰倂値丂丂(Nm)
丂倂値亖倗倣値丂(N)乮憤廳検乯
偱偁傝丄旕忢偵娙扨側幃偱昞偝傟傑偡丅
丂儌乕儊儞僩摉偨傝偺侾墌嬍偺忋柺偲壓柺偺孹偒偺嵎儮兤(rad)偼倛乛俤 I偱偡丅
偙偙偱I偼抐柺俀師儌乕儊儞僩偲屇偽傟丂兾倰4乛係偱偡丅
嵟忋柺傪孹偒侽丏侾俆(0.149rad)偱偁傞傛偆偵偟偰丂X(n)偵偦偭偰愊傒忋偘偰峴偒丄嵟壓柺偺孹偒偑侽偵側偭偨偲偙傠偑尷奅偱偡丅懄偪
atan(兪)亖乷乮値亄侾乯値乛俀乸*倰倗倣倛乛俤I
偱偡丅寁嶼偡傞偲
値亖俁俋俉俉俈丄俫亖係俈丏俉俇係倣丄倃亖侽丏侾侾侾俈倣
偱偡丅偡側傢偪丂侾侾們倣嫮偵側傝傑偡丅
側偍墌斦偑孹偄偰挘傝弌偟曽岦偵庒姳弅傓岠壥乮栺侽丏俇亾乯偲偐丄嵶偐偄偙偲傪尵偆偲妏偑弌擖傝偡傞偲偐偼柍帇偟傑偟偨丅
廳偝偑栺係侽倠倗倖偱丄嬥妟偼栺係枩墌偱偡偐傜丄H2儘働僢僩偺奿擺屔偁偨傝偱帋偣側偔偼側偄偱偡偹丅
亂俹丏俽丏亃
亂偍偪側偄亃偺慜採偲偟偰侾楍偵愊傒忋偘傞偲偄偆偺偑偁傝傑偡丅
偙傟傪偼偢偟偰丄暋悢楍傪儗儞僈暻偺傛偆偵愊傒忋偘偰儌乕儊儞僩傪娚榓偡傟偽亂偮傇傟側偄亃偺僆乕僟乕偵側傞偲巚偄傑偡丅懡暘丅
丂傑偨丄捵傟側偄侾墌嬍傪壖掕偟偰丄抧媴偺堷椡偲帺揮偵傛傞墦怱椡偺岠壥傪峫偊傞偲丄柺敀偄嬋慄偑摼傜傟傞偐傕丅
彮側偔偲傕愒摴柺忋偱偼惷巭塹惎婳摴乮俁俇侽侽侽倠倣乯埲忋偵偼愊傔側偄丅
仧弌戣幰偺僐儊儞僩丅
嶰恖偲傕嵟廔揑偵偼惓夝偱偡丅
摿偵Y.M.Ojisan 偝傫偺夝摎偵偼嬃偒傑偟偨丅
傑偝偐丒丒丒幚嵺偺暔棟揑惈幙傪嵶偐偔峫偊傞側傫偰偙偲傪偟偰偔偩偝傞偲偼偡偽傜偟偄偲巚偄傑偡丅