『0＆1四面体』解答

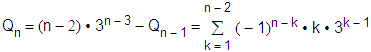
◆滋賀県　ippei　さんからの解答。

4つの数を10進数で0、1、2、3と表すと、
0000ができるのは201と並ぶときである。

n桁の数で連続した3桁はn-2箇所できる。

したがってどこにも201ができない確率は
(1− 1
27		 )n-2

よって求める極限はlog( 26
27		 )

◆山梨県　Footmark　さんからの解答。

解答といっても途中までですが、あしからず。

ippeiさんにならって、正四面体の各面にある数字を１０進数で表し、０,１,２,３とします。

この問題はサイコロを振るのとは違い、同一面が連続しない特徴があります。
最初、０の面が底面にあることを考慮すると、２０１が数列に存在する場合の数は以下となります

３回なら明らかに、201 の１通り。

４回なら次の５通り。
（２０１？のとき３通り)　2010 , 2012 , 2013
（？２０１のとき２通り)　1201 , 3201

５回なら次の２２通り。
（２０１？？のとき９通り)　20101 , 20102 , 20103 , 20120 , 20121 , 20123 , 20130 , 20131 , 20132
（？２０１？のとき６通り)　12010 , 12012 , 12013 , 32010 , 32012 , 32013
（？？２０１のとき７通り)　10201 , 13201 , 20201 , 21201 , 23201 , 30201 , 31201

ですから、２０１がどこにも存在しない確率は、
ｎ＝３のとき、１− １
３3
ｎ＝４のとき、１− ５
３4
ｎ＝５のとき、１− ２２
３5
となり、ippeiさんが示された (１− １
２７		 ) n-2 とは違うようです。

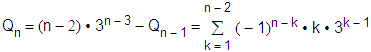
２０１が数列の複数箇所に存在するとき、それを重複して数えてよいのなら、ｎ回転がして２０１が存在する場合の数Ｑnは以下になります。

ところが、この式はｎ≧６のときは重複して数えているので、正しいＱnを上回っています。

正しいＱnさえ得ることができれば、
１−Ｐn＝１− Ｑn
３n
より、答えも出せる筈ですが、ここから先に進めません。^^;

◆大阪府　macsyma2e　さんからの解答。

qn＝1-pn and
rn＝事象「 n回後の列に‘100001’が存在せず、n回目の数字が‘10’である 」の確率 for all n∈{0,1,...}
とおくと、
q n+1 ＝q n -r n-1 ×( 1
3		 )2 and

r n ＝(q n-1 -r n-1 )×( 1
3		 )　for all n∈{1,2,...}

従って、
27×qn+2-18×qn+1-9×qn+qn-1＝0 for all n∈{1,2,...}
が成立するので、27x3-18x2-9x+1 の3根が
2
9		 + 2
9		 × ×cos( 1
3		 ×Arccos( 43
338		 × ))、

2
9		 + 2
9		 × ×cos( 1
3		 ×(2×π±Arccos( 43
338		 × )))．

であることに注意して、

　求める極限値
＝ 2
9		 + 2
9		 × ×cos( 1
3		 ×Arccos( 43
338		 × ))．

　『0＆1四面体』へ

　数学の部屋へもどる