『整数問題一発勝負 Part１』

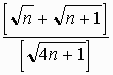
【問題１】

ピラミッド状に積まれたブロックがあります。
真上から見た図を

１
２１
３２１
４３２１

のように表しましょう。
４と書かれた部分には４個のブロックが積まれています。
するとこの場合のブロックの総数は20になります。

ではｎ段に積まれたブロックの場合、総数はいくつになりますか？

【問題２】

１２３４５６

７８９ 10 11 12

13 14 15 16 17 18

19 20 21 22 23 24

25 26 27 28 29 30

31 32 33 34 35 36

という風に36個の数が書き込んであります。

これらの中から１つ数を選んで○をつけます。
○をつけた数を含む行と列に関して、(○以外の)数を線を引いて消します。


　｜
　｜
―○―――
　｜
　｜

次に、線が引かれていない数を適当に選び○をつけて、上と同じように線を引きます。

これを繰り返すと、いくつか○がついて操作は終了しますが、○のついた数の合計は常に一定になります。
なぜでしょう？

また、○のついた数の合計が常に一定となるような、まったく別の36個の配列を考えてみて下さい。
余力がある人は何通りあるか etc...

【問題３】

任意の自然数ｎに対して

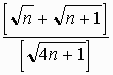
の値は一定になります。
なぜでしょう？

[　]はガウス記号です。