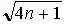 、
、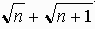 のいずれも正の数であること、
のいずれも正の数であること、ならびに
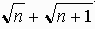 は無理数なので自然数にはならないこと(背理法を用いて簡単)に注意する。
は無理数なので自然数にはならないこと(背理法を用いて簡単)に注意する。◆石川県 平田和弘 さんからの解答。
(問題1解答)
第n段目をanとすると、
an−an-1=n の関係があるので
| 一般項は、an= | 1 ― 2 | ・n(n+1) と求められる。 |
| 総数= | n Σ K=1 | 1 ― 2 | k(k+1)= | 1 ― 6 | n(n+1)(n+2) |
(問題2解答)
まず列(横の並び)で見ると、6で割った余りで分類したものとみます。
このとき、第6列は1回りしていることに注意して、各列1回ずつ現れるので、
また、行(縦の並び)で見ても、
(6×○+□)という形の数のうち、○は0から5が必ず1回ずつ現れているので、
a1、a2、・・・a6を互いに異なり、かつ、0から5のどれかとして・・・(A)
総和
=[6a1+6a2+6a3+6a4+6a5+6{a6+1}]
という形であらわせるので、
総和=6{a1+a2+a3+a4+a5+a6}+21
このうち、a1+a2+a3+a4+a5+a6は、(A)より15になるので、
総和=6・15+21=111 で一定となる。
他の例は、対称性(?)を利用して
1. 行(縦の並び)と列(横の並び)を入れ替えたもの。
| 1 | 7 | 13 | 19 | 25 | 31 |
| 2 | 8 | 14 | 20 | 26 | 32 |
| 3 | 9 | 15 | 21 | 27 | 33 |
| 4 | 10 | 16 | 22 | 28 | 34 |
| 5 | 11 | 17 | 23 | 29 | 35 |
| 6 | 12 | 18 | 24 | 30 | 36 |
2. 36から1まで逆に横に順に並べたもの。
| 36 | 35 | 34 | 33 | 32 | 31 |
| 30 | 29 | 28 | 27 | 26 | 25 |
| 24 | 23 | 22 | 21 | 20 | 19 |
| 18 | 17 | 16 | 15 | 14 | 13 |
| 12 | 11 | 10 | 9 | 8 | 7 |
| 6 | 5 | 4 | 3 | 2 | 1 |
8通りはすぐに考えられます。
(問題4)
1になることはわかりますが証明ができません。
◆広島県 清川 育男 さんからの解答。
【問題1】
| 答え n+2C3= | 1 6 | n(n+1)(n+2) |
「正三角形の個数は?」の立体版ですかね。
| n+2C4= | 1 24 | (n−1)n(n+1)(n+2) n≧2 |
「もうひとつの算数チャレンジ」で話題になりました。
【問題2】
6行6列>5行5列>4行4列>3行3列>2行2列>1行1列
5回の操作で6個の数字を選んで終わる。
重複した数はないので、結局1から36までの合計を6等分したことになる。
(論理的飛躍?)。
(1+36)×36÷2÷6
=37×3
=111
元の6行6列の正方行列の
ある行とある行を交換しても成り立つ。
ある列とある列を交換しても成り立つ。
1つの6行6列の正方行列から6個の同一?のものが出来る。
6!×6!÷6
=6!×5!
=720×120
=86400
86400通りでしょうか?
(1〜36の数字を使うとして)
1〜36にこだわらなければ、連続した36個の数字を問題のように入れていけばよいと思います。
【問題3】
分子、分母をルートNで割る。
与式=1
【出題者のコメント】
【問題1】は清川さんのおっしゃるとおり本質的には
n+2C3となります。
【問題3】ガウス記号を取ったら大小関係はどうなっているか?を出発点にして考えるといいかも。
◆滋賀県 一平ちゃん さんからの解答。
【問題1】
和をS(n)とする。
S(n)=1・n+2・(n−1)+・・・・+n・1
| = | n Σ K=1 | k(n+1-k) |
| = | 1 ― 6 | n(n+1)(n+2) |
◆海外 nymc さんからの解答。
【問題3】
以下、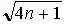 、
、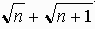 のいずれも正の数であること、
のいずれも正の数であること、
ならびに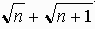 は無理数なので自然数にはならないこと(背理法を用いて簡単)に注意する。
は無理数なので自然数にはならないこと(背理法を用いて簡単)に注意する。
まず分母と分子のガウス記号内の式の大小関係は、
分子の式>分母の式。
なぜなら、
(分子の式)2
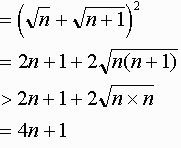
= (分母の式)2
ここで次の事実が成り立つ。
kをある自然数としたとき、
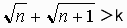 ならば
ならば 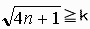 …(*)
…(*)
(*)は、分子の式 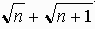 がある自然数kを越えていると、それより小さい数である分母の式
がある自然数kを越えていると、それより小さい数である分母の式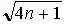 も同時にその自然数k以上になることを示している。
も同時にその自然数k以上になることを示している。
したがってそれらの整数部分は同じ値をとることになる。
よって、求める答えは「1」。
(*)の証明:
(*)の対偶
kをある自然数として、
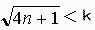 ならば
ならば 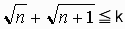 を証明する。
を証明する。
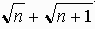 は無理数なので実際には等号は成立しないはずだが、以下ではそれも同時に示される。
は無理数なので実際には等号は成立しないはずだが、以下ではそれも同時に示される。
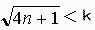 ならば、両辺を二乗して
ならば、両辺を二乗して
4n+1< k2
左辺4n+1は自然数なので4n+1≦k2-1、
よって4n+2≦k2
ここで
| ( | 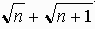 | ) | 2 |
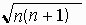
上では相加相乗平均不等式を用いた。
nとn+1はもちろん等しくないので等号は成立しない。
以上、(*)の対偶が成立することが示された。
(以上終り)
◆京都府 the king of water gate さんからの解答。
【問題1】
0≦x≦y≦z<nとなる整数の組(x,y,z)の個数で
0≦x≦y≦z<n ⇔ 0<x+1<y+2<z+3<n+3となるので
| ( | n+2 3 | )= | n(n+1)(n+2)
6 | 。 |
【問題2】
36個の数の位置を0以上6未満の整数x,yを使って
(x,y)と表すことにする。
選ばれた数がn個(0≦n<6)のときは
それらの位置を(xi,yi)(0≦i<n)とすると
0以上6未満の整数でxi(0≦i<n)の全てと異なる整数xと
0以上6未満の整数でyi(0≦i<n)の全てと異なる整数yがあり
(x,y)にある数を選ぶことができる。
選ばれた数が6個のときは
それらの位置を(xi,yi)(0≦i<6)とすると
どの(x,y)もx=xiとなるiがあるので、それ以上選ぶことはできないので、選ばれる数は常に6個になる。
36個の数全てに同じ数を足しても選ばれる数の合計が一定であるという性質は変わらないので、
−1を足して0以上36未満の整数とします。
0の位置を(s,t)とし
(i,t)(0≦i<6)にある数をpi
(s,i)(0≦i<6)にある数をqi
(x,y)にある数をr(x,y)とする。
(x,y)をx≠s,y≠tとなる位置とし
0以上6未満の整数でs,xと異なる数をxi(0≦i<4)
0以上6未満の整数でt,yと異なる数をyi(0≦i<4)とすると
| r(s,t)+r(x,y)+ | Σ 0≦i<4 | r(xi,yi) |
| =r(x,t)+r(s,y)+ | Σ 0≦i<4 | r(xi,yi) なので |
r(x,y)=px+qy。
x≠s,y≠tのとき
r(x,t)=px+qt。
r(s,y)=ps+qy。
r(s,t)=ps+qt。
よってどの(x,y)についても
r(x,y)=px+qyとなる。
逆にこのとき選ばれる数の合計は
常にΣpi+Σqiで一定になる。
問題にある並べかたはこのようになっているので、選ばれる数の合計は常に一定になる。
a∈N0,b∈N0,a|bのとき
Mab={i|i∈Z,0≦i<b,a|i}とし
A,BがA⊂N0,B⊂N0
a∈A,b∈B,c∈A,d∈B,
a+b=c+d→(a,b)=(c,d)のとき、
A*Bを
A*B={a+b|a∈A,b∈B}とする。
A⊂N0,B⊂N0,
M136=A*B,|A|=|B|=6
となるA,Bの組の個数をe個とすると
問題の条件に合う1以上36以下の整数の並べかたは
全部で6!×6!×e通りになる。
M136 ={ 0, 1, 2, 3, 4, 5}*{ 0, 6,12,18,24,30} ={ 0, 1, 2, 6, 7, 8}*{ 0, 3,12,15,24,27} ={ 0, 1, 2, 9,10,11}*{ 0, 3, 6,18,21,24} ={ 0, 1, 2,18,19,20}*{ 0, 3, 6, 9,12,15} ={ 0, 1, 4, 5, 8, 9}*{ 0, 2,12,14,24,26} ={ 0, 1, 6, 7,12,13}*{ 0, 2, 4,18,20,22} ={ 0, 1,12,13,24,25}*{ 0, 2, 4, 6, 8,10}となるのでe=14。
6!×6!×14=7257600。
| 24 | 12 | 0 | 2 | 14 | 26 | |
|---|---|---|---|---|---|---|
| 8 | 33 | 21 | 9 | 11 | 23 | 35 |
| 4 | 29 | 17 | 5 | 7 | 19 | 31 |
| 0 | 25 | 13 | 1 | 3 | 15 | 27 |
| 1 | 26 | 14 | 2 | 4 | 16 | 28 |
| 5 | 30 | 18 | 6 | 8 | 20 | 32 |
| 9 | 34 | 22 | 10 | 12 | 24 | 36 |
(1)
A*B,B*Aのどちらかが存在すれば、もう一方も存在して
A*B=B*A。
(2)
(A*B)*C,A*(B*C)のどちらかが存在すれば、もう一方も存在して
(A*B)*C=A*(B*C)。
(3)
A*{0}={0}*A=A。
(4)
M136は{0}を使わずさらに分解できて
M136 =M12*M24*M412*M1236 =M12*M26*M612*M1236 =M12*M26*M618*M1836 =M13*M36*M612*M1236 =M13*M36*M618*M1836 =M13*M39*M918*M1836。(5) N0→N0の関数f,gに対してf*gを
| (f*g)(n)= | Σ i+j=n | f(i)g(j) と定義し |
A⊂N0に対してfaを
fa(n)=0(n∈Aでない)
fa(n)=1(n∈A)
と定義すると、
A*Bが存在する ⇔ ∀n((fa*fB)(n)≦1)となりこれらが成り立つとき
(6) qi(0≦i)が全て素数のとき
N0=M1q0*Mq0q0q1*Mq0q1q0q1q2*...。
(8)
N×Nに並べた数が問題2の条件を満たす。⇔(x,y)=px+qyと表される。であり N×N×Nなどでも同じような問題が考えられる。
【問題3】
4n+1
=n+2n+(n+1)
| ≦n+2 | 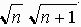 | +(n+1) |
| =( | 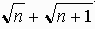 | ) | 2 |
4n+2は平方数でないので
m2<4n+2<(m+1)2
となる整数mがある。
m2≦4n+1<4n+2<4n+3≦(m+1)2。
m2≦4n+1
| ≦( | 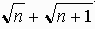 | ) | 2 |
| m≦ | 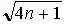 | ≦ | 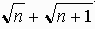 | <m+1。 |
よって
| m=int( | 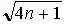 | )=int( | 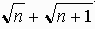 | ) |
なので1になる。