◆愛知県 Y.M.Ojisan さんからの質問。
【問題2】の定義で分かりにくいところがあります。
私の理解するところでは、P=2のとき、下記のようになります。
黄色部分が問題2−2と合いません。
K桁(緑)の定義および並べ方のどこに間違いがあるのでしょうか。
| P=2 | 並べ方? | 桁定義? |
|||||
| P3 | P2 | P | 1 | 値 | N | K! | N K! |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
|
| 0 | 0 | 1 | 0 | 2 | 2 | 1 | 2 |
| 0 | 0 | 1 | 1 | 3 | 3 | 1 |
|
| 0 | 0 | 2 | 0 | 4 | 4 | 1 | 4 |
| 0 | 1 | 0 | 0 | 4 | 5 | 2 | 2.5 |
| 0 | 0 | 2 | 1 | 5 | 6 | 1 |
|
| 0 | 1 | 0 | 1 | 5 | 7 | 1 |
|
| 0 | 1 | 1 | 0 | 6 | 8 | 1 | 8 |
| 0 | 1 | 1 | 1 | 7 | 9 |
1 |
|
| 0 | 1 | 2 | 0 | 8 | 10 | 1 | 10 |
| 0 | 2 | 0 | 0 | 8 | 11 | 2 | 5.5 |
| 1 | 0 | 0 | 0 | 8 | 12 | 6 | 2 |
【コメント】
問題2−2に勘違いがあったそうなので、削除しました。
◆広島県 清川 育男 さんからの解答。
【問題1】
P4+P6+P7+P8+P9+P10
2000(10)=11111010000(2)
1+P+P2+P3+・・・+Pn-1
| = | pn-1 p-1 | <pn |
◆愛知県 Y.M.Ojisan さんからの質問。
以下において0dXXXXないしXXXX はXXXXを10進数とみなすことを示す。
また、0bXXXX , 0pXXXX , 0!XXXX はそれぞれ 2進、p進、階乗進数とする。
【問題1】
0d2000 = 0b11111010000 である。
0bα>0bβ ならば p≧2 のとき 0pα>0pβ であるから、2進の大小関係は問題1の制限内のp進数に対しても等価である.
従って、2000番目は 0p11111010000 である。
若干変形して
| 2000番目=p4+ | p6(p5−1) p−1 |
【問題2】
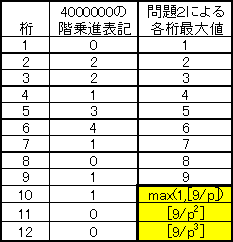
0d20002= 0d4000000 = 0!1101431220 であり、
20002は階乗進数で10桁である。
従って、それ以下の階乗進数において各桁値の最大値は下表のように「9」である。
すなわちp≧10であれば、
0!α>0!β ならば 0pα>0pβ であるから、階乗進の大小関係は問題2の制限内のp進数に対しても等価である.
なお、説明は略するが
p=9の場合もたまたま0!1101431220との大小関係は維持される。
従って、p≧9のとき
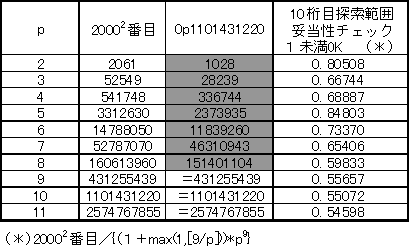
20002番目= 0p1101431220 である。

p<9の場合は一般解は??ですが、これぐらいならパソコンであっというまに計数可能なので、単純に数えました。
但しpが小さいと上位桁から落ちてくるものが有るので、上表の黄色枠まで広げて探索し、結果と照らして十分であることを確認しています。
結果を下表に示します。