仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
亂栤戣侾亃
寢壥偼偙偪傜偱偡丅
亂栤戣俀亃
A B C D E F G H I
1) 1 9 6 8 2 4 5 7 3
2) 1 9 8 6 4 2 5 3 7
3) 1 6 9 5 2 7 8 4 3
4) 1 8 9 5 4 3 6 2 7
5) 2 9 7 6 5 1 4 3 8
6) 2 7 9 4 5 3 6 1 8
7) 3 7 4 8 2 6 5 9 1
8) 3 4 7 5 2 9 8 6 1
9) 3 8 7 5 6 1 4 2 9
10) 3 7 8 4 6 2 5 1 9
11) 4 9 3 8 5 1 2 7 6
12) 4 3 9 2 5 7 8 1 6
13) 6 7 1 8 5 3 2 9 4
14) 6 1 7 2 5 9 8 3 4
15) 7 3 2 6 4 8 5 9 1
16) 7 2 3 5 4 9 6 8 1
17) 7 6 3 5 8 1 2 4 9
18) 7 3 6 2 8 4 5 1 9
19) 8 3 1 6 5 7 4 9 2
20) 8 1 3 4 5 9 6 7 2
21) 9 2 1 5 6 7 4 8 3
22) 9 4 1 5 8 3 2 6 7
23) 9 1 2 4 6 8 5 7 3
24) 9 1 4 2 8 6 5 3 7
僾儘僌儔儉傪慻傫偱夝偒傑偟偨丅亂偍傑偗偺栤戣亃
傕偟梌幃偑廂懇偟偰嬌尷抣傪帩偮偲偟偨応崌偦偺嬌尷抣傪俽偲偡傞丅
丂俽亖侾亄俽俻俼俿乮侾亄俽乯
丂俽2亅俁俽亖侽
丂俽乮俽亅俁乯亖侽
丂俽亜侽偱偁傞偐傜 俽亖俁
廂懇忦審偑傢偐傝傑偣傫丅
係侽崁傑偱僐儞僺儏乕僞偱寁嶼偟偨偲偙傠偱偼娫堘偄偼側偄偲巚偄傑偡偑丄丄丄丅
仧戝嶃晎丂忋尨丂岹擵 偝傫偐傜偺夝摎
亂栤戣侾亃
倎乣倝丂偺榓偼係俆丏
傛偭偰
a+b+c=d亄e+f+=g+h+i亖15
1偐傜9傪巊偭偰榓偑15偲側傞慻傒崌傢偣偼埲壓偺偺8捠傝
乮1,5,9乯乮1,6,8乯乮2,4,9乯乮2,5,8乯
乮2,6,7乯乮3,4,8乯乮3,5,7乯乮4,5,6乯
偙偙偱丂戣堄傪枮偨偡偺偼
乮1,5,9乯乮2,6,7乯乮3,4,8乯丒丒丒僷僞乕儞嘥
傕偟偔偼
乮1,6,8乯乮2,4,9乯乮3,5,7乯丒丒丒僷僞乕儞嘦
傪巊偭偨偲偒丅
傛偭偰
丂1+5+9=2+6+7=3+4+8
傕偟偔偼
1+6+8=2+4+9=3+5+7
亂栤戣俀亃
ACD,BEF,GHI傪捀揰偲偡傞嶰妏宍傪栤戣侾偺僷僞乕儞嘥傪巊偭偰嶌傞側傜
ABG,CEH,DFI傪捀揰偲偡傞嶰妏宍偼僷僞乕儞嘦傪巊偆偙偲偵側傞丅
偡傞偲丄DEG傪捀揰偲偡傞嶰妏宍偼丂榓偑15偲側傞俉偮偺慻傒崌傢偣偺偆偪丄僷僞乕儞嘥丄嘦偱巊傢側偐偭偨
乮俀丆俆丆俉乯偐乮係丆俆丆俇乯傪巊偄丄嶌傞偙偲偵側傞丅
偙偙偱丂DEG傪乮2,5,8乯傪巊偭偰丂嶌偭偰傒傞丅
揔摉偵丂D=2丂E=5丂G=8丂偲偡傞丅
D=2傛傝丂A偼丂嶰妏宍ACD偼僷僞乕儞嘥傪巊偆偺偱丄6偐7偲側傞偑丄
嶰妏宍ABG傪傒偨偲偒偵A=7偲偡傞偲丄B=0偲側傝晄壜丅
傛偭偰丄A=6丂偲側傞丅
偙偙傑偱弌偒傞偲丂屻偼榓偑15傪巊偭偰偳傫偳傫杽傑偭偰偄偔丅
A=6傛傝C=7丏
嶰妏宍AGB傪傒傞偲巆傝偺B=1丏
嶰妏宍BEF偵偍偄偰巆傝偺F=9
嶰妏宍CEH偱偼巆傝偺H=3丏
嶰妏宍GHI偱I=4
傛偭偰
(A,B,C,D,E,F,G,H,I)=(6,1,7,2,5,9,8,3,4)
偪側傒偵丄嶰妏宍DEG傪乮4,5,6乯傪巊偭偨偲偒傕弌棃傑偟偨丅
仧愇愳導丂暯揷丂榓峅 偝傫偐傜偺夝摎
亂栤戣侾亃
1+6+8亖2+4+9亖3+5+7
1+5+9亖2+6+7亖3+4+8
2,5,8傪1曈偵廤傔傞(2+5+8偵偡傞)偲偱偒側偄丅
亂栤戣俀亃
A亖1丄B亖9丄C亖6丄D亖8丄E亖2丄F亖4丄G亖5丄H亖7丄I亖3
4偮偺彫偝側擇摍曈嶰妏宍
丂A+C+D亖1+6+8亖15
丂B+E+F亖9+2+4亖15
丂D+E+G亖8+2+5亖15
丂G+H+I亖5+7+3亖15
3偮偺戝偒側擇摍曈嶰妏宍
丂A+B+G亖1+9+5亖15
丂C+E+H亖6+2+7亖15
丂D+F+I亖8+4+3亖15
亂栤戣俀亃
僾儘僌儔儉偵傛傝媮傔傑偟偨丅
A丂B丂C丂D丂E丂F丂G丂H丂I 1丂6丂9丂5丂2丂7丂8丂4丂3 1丂8丂9丂5丂4丂3丂6丂2丂7 1丂9丂6丂8丂2丂4丂5丂7丂3 1丂9丂8丂6丂4丂2丂5丂3丂7 2丂7丂9丂4丂5丂3丂6丂1丂8 2丂9丂7丂6丂5丂1丂4丂3丂8 3丂4丂7丂5丂2丂9丂8丂6丂1 3丂7丂4丂8丂2丂6丂5丂9丂1 3丂7丂8丂4丂6丂2丂5丂1丂9 3丂8丂7丂5丂6丂1丂4丂2丂9 4丂3丂9丂2丂5丂7丂8丂1丂6 4丂9丂3丂8丂5丂1丂2丂7丂6 6丂1丂7丂2丂5丂9丂8丂3丂4 6丂7丂1丂8丂5丂3丂2丂9丂4 7丂2丂3丂5丂4丂9丂6丂8丂1 7丂3丂2丂6丂4丂8丂5丂9丂1 7丂3丂6丂2丂8丂4丂5丂1丂9 7丂6丂3丂5丂8丂1丂2丂4丂9 8丂1丂3丂4丂5丂9丂6丂7丂2 8丂3丂1丂6丂5丂7丂4丂9丂2 9丂1丂2丂4丂6丂8丂5丂7丂3 9丂1丂4丂2丂8丂6丂5丂3丂7 9丂2丂1丂5丂6丂7丂4丂8丂3 9丂4丂1丂5丂8丂3丂2丂6丂7
(姶憐)
忋婰偑偡傋偰偐偳偆偐偼専徹偡傞弍偑偁傝傑偣傫偑丄妋偐偵嵟弶夝摎偟偨摎偊傕偙偺拞偵偼偁傝傑偡丅
嵟弶嶌惉偟偨僾儘僌儔儉偱偼傑傞侾擔(俀係帪娫)偨偭偰傕専嶕廔椆偟傑偣傫偱偟偨丅
偦傟偐傜丄俀擔娫傾儖僑儕僘儉傪夵椙偟偰俁帪娫懌傜偢偱専嶕廔椆偱偒傞傛偆偵側傝傑偟偨丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣俀亃
丂俉丂丂丂侾
俁丂係丂俆丂俋
俇丂丂
丂丂俈丂俀
亂姶憐亃
偝偡偑傾僀儞僔儏僞僀儞両偲偰傕旤偟偄丅
侾尭偠偰丄俁恑悢偺奺埵偛偲偵峫偊傟偽椙偄偙偲偵婥偑晅偄偨偺偱丄寢峔僄儗僈儞僩偵夝偗偨丅
亂偍傑偗偺夝摎亃
俁
亂奣棯夝亃
僄儗僼傽儞僩偵偟偐夝偗偢丄彂偔偺偑戝曄側偺偱戝嬝偩偗丅
丂丂丂
丂
亂姶憐亃
偙偺傛偆側暋嶨側幃偑丄堦斒揑乮倣偱乯偵惍悢偵廂懇偡傞偲偼偲偰傕柺敀偄丅
仧恄撧愳導丂偄傢偟 偝傫偐傜偺夝摎
亂栤戣俀亃
| 俙 | 俛 | 俧 |
| 俠 | 俤 | 俫 |
| 俢 | 俥 | 俬 |
傑偨偼
| 俥 | 俬 | 俢 |
| 俛 | 俧 | 俙 |
| 俤 | 俫 | 俠 |
傑偨偼
| 俫 | 俠 | 俤 |
| 俬 | 俢 | 俥 |
| 俧 | 俙 | 俛 |
偲偄偆杺曽恮傪嶌傟偽傛偔丄3亊3偺杺曽恮偼杮幙揑偵
| 俉 | 侾 | 俇 |
| 俁 | 俆 | 俈 |
| 係 | 俋 | 俀 |
偺1捠傝偱丄夞揮丒棤曉偟傪峫偊偰8捠傝偱偡偐傜丄
慡晹偱24捠傝偺摎偊偑偁傞偙偲偵側傝傑偡丅
亂栤戣俁亃
x亞0, n亞0, a亞0, k傪晧偱側偄惍悢偲偟偰
f(k) = (x亄kn)亄(n亄a)
偲偍偒傑偡丅
丂f(k)2
= (x亄kn)2亄2 (n亄a) (x亄kn)亄(n亄a)2
= a (x亄kn)亄(n亄a)2亄(x亄kn) f(k亄1)傛傝
![]()
偱偡丅偙傟傪
f(0) = x亄n亄a
偵嵞婣揑偵戙擖偡傞偲
![]()
偙偙偱x=2, n=1, a=0偲偍偗偽丄
(梌幃)=3傪摼傑偡丅
師偺娭學幃傕丄儔儅僰僕儍儞偑敪尒偟偨傕偺偩偦偆偱偡丅
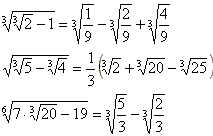
仧帬夑導丂CsR 偝傫偐傜偺夝摎
亂栤戣俀亃
A偐傜I傑偱偺憤榓偼45偱偁傞偙偲丄偦偟偰偦傟偧傟9埲壓偺堎側傞帺慠悢偱偁傞偙偲偐傜丄懌偟偰15偵側傞慻傒崌傢偣傪峫偊傞丅
傑偢丄侾丄俀丆俁偼偦傟偧傟暿偺慻偵擖傞偙偲偼帺柧丅
亙侾偺慻亜
1+5+9丂仺a
1+6+8丂仺b
亙俀偺慻亜
2+4+9丂仺c
2+5+8丂仺d
2+6+7丂仺e
亙俁偺慻亜
3+4+8丂仺f
3+5+7丂仺g
埲忋偺慻傒崌傢偣偑峫偊傜傟傞丅
摨偠悢偑擖傜側偄慻傒崌傢偣偼丄a偲e偲f偺慻丄偦偟偰丄b偲c偲g偺慻偱偁傞偙偲偑傢偐傞丅
傛偭偰丄
1+5+9
=2+6+7
=3+4+8
=15
傑偨丄
1+6+8
=2+4+9
=3+5+7
=15偲偄偆偙偲偑傢偐偭偨丅
偙偙偱丄栤戣偺恾傪幃偱偁傜傢偡偲丄
A+B+G
=C+E+H
=D+F+I
=15丂仺@
A+C+D
=B+E+F
=G+H+I
=15丂仺A
D+E+G=15丂仺B
偲側傝丄愭傎偳媮傔偨慻傒崌傢偣偵@偐A偺偳偪傜偐偑偦傟偧傟擖傞偙偲偵側傞丅
徠傜偟崌傢偣傞偲丄
傑偢A=1丄E=2丄I=3偱偁傞偙偲偑傢偐傞偺偱丄
@傛傝丄
B+G=14
C+H=13
D+F=12
A傛傝丄
C+D=14
B+F=13
G+H=12
B傛傝丄
D+G=13
偑惉棫丅偙傟傪楢棫曽掱幃乮傂偲偮梋寁偩偗偳乯偲偟偰夝偔偲丄
A=1
B=9
C=6
D=8
E=2
F=4
G=5
H=7
I=3
偑媮傔傜傟傞丅
偙傟傪恾偵憓擖偡傟偽丄摎偊偵側傞丅
丂仧丂栤戣傊傕偳傞
丂仧丂崱廡偺栤戣傊
丂丂