『今週の問題』

『今週の問題』第236回　解答

◆福岡県　うぃん　さんからの解答


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　━
┃　┃　┃　┃　┃　┃　
　‥　━　‥　‥　‥
┃　：　：　┃　┃　┃　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

考え方：

まず、「０」と「３」が並んでいるところは、「０」に接していない「３」の辺すべてを通る。
この辺を基点として「０」や交差しないなどの条件を元に辺を通る部分をある程度確定すると以下のようになる。

　‥　‥　‥　‥　‥
：　：０：　：０：　：　
　━　‥　━　‥　‥
┃　┃３┃　┃　：３：　
　‥　━　‥　‥　‥
┃　：　：２：　：　：　
　‥　‥　‥　‥　‥
：３：　：　：２：　：　
　‥　‥　‥　‥　‥
：　：１：　：２：　：　
　‥　‥　‥　‥　‥

また、右上の「０」「３」が斜めに並んでいるところでは、「３」のした以外の辺が通らないとすると、「０」の辺を通ることになるので、「３」の下以外と通ることがわかる。
これを基点に他の通る辺をある程度確定する。
また、中央の「２」は上や左と通ると交差するので、右と下を通ることがわかる。
ここまでをまとめると以下のようになる。

　‥　‥　‥　‥　‥
：　：０：　：０：　：　
　━　‥　━　‥　━
┃　┃３┃　┃　┃３┃　
　‥　━　‥　‥　‥
┃　：　：２┃　：　┃　
　‥　‥　━　‥　‥
：３：　：　：２：　：　
　‥　‥　‥　‥　‥
：　：１：　：２：　：　
　‥　‥　‥　‥　‥

左下の「３」の上の辺を通過しないとすると、そのままループになってしまうので、「３」の左側が通らない辺となる。これを基点にさらに進ませると…


　‥　‥　‥　‥　‥
：　：０：　：０：　：　
　━　‥　━　‥　━
┃　┃３┃　┃　┃３┃　
　‥　━　‥　‥　‥
┃　：　：２┃　┃　┃　
　━　‥　━　‥　‥
：３┃　┃　：２┃　┃　
　━　‥　━　━　‥
┃　：１：　：２：　┃　
　━　━　━　━　━

となる。

【感想】

よくあるパズルゲームの簡単なバージョンですね。

◆群馬県　天10　さんからの解答


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　━
┃　┃　┃　┃　┃　┃　
　‥　━　‥　‥　‥
┃　：　：　┃　┃　┃　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

ニコリの「スリザーリンク」と内容は一緒ですね。
このパズル好きで時間を忘れて没頭することがしばしばあります。

【考え方】

ループし、交差したり、分かれることはないという条件から、線が交わっている点には、コースとして通ればコースとなる辺が２つ交わり、まったく通らなければコースとなる辺は無しとなることが分かります。
コースとして２辺が引かれた点の残りの辺は通らない辺となります。

ある点において、未確定の辺が１つの場合、コースとなる辺が１つの場合、その実確定の辺はコースとなります。
その他の場合（コースとなる辺が０または２）はコースとはなりません。

紙上で行う場合ならコースとなりえない辺にｘマークをつけるなどして区別させると解きやすいでしょう

（１）まずは、数字「０」に着目します。
数字０の周りの4辺は線が引けないので引けないとマークします。
連鎖で引けない部分が分かりますので、合せて引けないとマークしていきます。


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・　・ｘ・　・ｘ・　・
　　　３　　　　　３　
・　・　・　・　・　・
　　　　　２　　　　　
・　・　・　・　・　・
　３　　　　　２　　　
・　・　・　・　・　・
　　　１　　　２　　　
・　・　・　・　・　・

（２）左側の０の下の３

既に上辺がコースになりえない状態で、コースになりえる辺が３つなので、残りの部分がコースになりえる辺として線を引きます。
連鎖で引ける辺が分かりますので、辺を引いていきます。


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・━・ｘ・━・ｘ・　・
┃　┃３┃　┃　　３　
・ｘ・━・ｘ・　・　・
┃　ｘ　ｘ２　　　　　
・　・　・　・　・　・
　３　　　　　２　　　
・　・　・　・　・　・
　　　１　　　２　　　
・　・　・　・　・　・

（３）中央の２

上辺と左辺がコースとなりえない辺である為、右辺とした辺が確定
さらに右下の２も同様


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・━・ｘ・━・ｘ・　・
┃　┃３┃　┃　　３　
・ｘ・━・ｘ・ｘ・　・
┃　ｘ　ｘ２┃　　　　
・　・　・━・ｘ・　・
　３　　　　ｘ２┃　　
・　・　・　・━・ｘ・
　　　１　　　２ｘ　　
・　・　・　・　・　・

（４）右上の３

上辺をコースとならないと仮定すると左右の辺もコースではない辺となり、コースとなる辺の数が矛盾するので、上辺はコースとなる。


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・━・ｘ・━・ｘ・━・
┃　┃３┃　┃　┃３┃
・ｘ・━・ｘ・ｘ・ｘ・
┃　ｘ　ｘ２┃　┃　┃
・　・　・━・ｘ・ｘ・
　３　　　　ｘ２┃　┃
・　・　・━・━・ｘ・
　　　１　　ｘ２ｘ　┃
・　・　・━・━・━・

（５）下の１

右側に辺に線を引くとループが複数となる為、引けないとマーク


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・━・ｘ・━・ｘ・━・
┃　┃３┃　┃　┃３┃
・ｘ・━・ｘ・ｘ・ｘ・
┃　ｘ　ｘ２┃　┃　┃
・　・ｘ・━・ｘ・ｘ・
　３　　┃　ｘ２┃　┃
・　・ｘ・━・━・ｘ・
┃　ｘ１ｘ　ｘ２ｘ　┃
・━・━・━・━・━・

（６）下の３左辺に線を引くと仮定すると、コースとなる辺の数が矛盾するので、引けない場所とマークする


・ｘ・ｘ・ｘ・ｘ・ｘ・
ｘ　ｘ０ｘ　ｘ０ｘ　ｘ
・━・ｘ・━・ｘ・━・
┃　┃３┃　┃　┃３┃
・ｘ・━・ｘ・ｘ・ｘ・
┃　ｘ　ｘ２┃　┃　┃
・━・ｘ・━・ｘ・ｘ・
ｘ３┃　┃　ｘ２┃　┃
・━・ｘ・━・━・ｘ・
┃　ｘ１ｘ　ｘ２ｘ　┃
・━・━・━・━・━・

◆埼玉県　数学好きＳＥ　さんからの解答


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　━
┃　┃　┃　┃　┃　┃　
　‥　━　‥　‥　‥
┃　：　：　┃　┃　┃　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

【考え方】

まず、(2,2)の位置にある「３」に着目する。
この正方形の４辺のうち、上の辺は「０」の正方形と共有しているので、ここはコースにならない。
したがって、残りの３辺がコースになる。

また、この「３」の左上の頂点から進める方向は左しかない。
（上に進むと「０」の辺に重なってしまう）
さらにそこから上に進むと袋小路に陥ってしまうため、下にしか進めない。
その先は、右に進むと(2,1)の正方形を囲む小さなループができてしまうため、ここも下にしか進めない。

(2,2)の右上の頂点についても同様の議論により、右→下という進路が確定する。

ここまでで、下図のようになる。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

次に、(3,3)の「２」に着目する。
上の辺がコースだとすると、(2,3)を囲む小さなループができてしまう。
また、左の辺がコースだとすると、枝分かれが発生してしまう。
よって、これらはコースではなく、右の辺と下の辺がコースになる。

次に、(4,1)の「３」に着目する。
もし、この正方形の上の辺と左の辺が同時にコースになると枝分かれが発生する。
したがって、これら２辺のうち、少なくとも片方はコースではない。
すなわち、下の辺と右の辺は必ずコースになる。

ここまでで、下図のようになる。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　‥　‥　━　‥　‥
：　┃　：　：　：　：　
　━　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

ここで、(4,1)の「３」の左の辺がコースだとすると、この正方形の右上の頂点から進む先がなくなってしまう。
（上に進むと枝分かれが発生し、右に進むとループが閉じてしまう。）

よって、ここはコースではなく、上の辺がコースになる。
左の辺がコースではないので、この正方形の左下の頂点からは下→右としか進めない。
また、そこから上に進むと(5,1)を囲むループができるため、右にしか進めない。
(5,2)は「１」なので、そこから上には進めず、その先も右に進むしかない。
反対側の端である(3,3)の「２」の左下の頂点からは下にしか進めない。
（左に進むと枝分かれが発生する）
(5,2)が「１」なので、その先は右にしか進めない。

ここまでで、下図のようになる。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　━　‥　━　‥　‥
：　┃　┃　：　：　：　
　━　‥　━　‥　‥
┃　：　：　：　：　：　
　━　━　━　‥　‥

(5,4)の「２」の左上の頂点から、上に進むと(4,3)を囲むループができてしまい、下に進むとループが閉じてしまうため、右にしか進めない。
同様に左下の頂点からも、右にしか進めない。
(5,4)は「２」であるため、右下の頂点からは右にしか進めず、その先は角なので上にしか進めない。
そこからは、左に進むとループが閉じてしまうため、上にしか進めない。

同様に、(5,4)の右上の頂点からも上にしか進めない。

ここまでで、下図のようになる。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

あとは、どちらの端に着目しても上→上としか進めない。
（曲がろうとすると、枝分かれができるか、ループが閉じてしまう。）
最後に、(2,5)の「３」の上の辺を通って端と端をつなげばループが完成する。

【感想】

絶対にコースになるところ、ならないところをきちんと確認していけば、特に問題なく解けると思います。
ただ、それを解答として記述するのが難しかったです。
黒板を使って口頭で説明するなら、きっと簡単だと思うのですが。

◆東京都　明　さんからの解答


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　━
┃　┃　┃　┃　┃　┃　
　‥　━　‥　‥　‥
┃　：　：　┃　┃　┃　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

【考え方】

最初に２行２列にある「３」と、すぐ上にある「０」に着目すれば「３」の回りのコースがまず決定できます。
さらにコースが単一のループを作らなければいけないことと、「０」の回りを通ってはいけないことから、次のコースが決定されます。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

３行３列の「２」の回りのコースの取り方は下記の一通りです。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　‥　‥　━　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

このコースの先を左へ延ばすと４行１列の「３」により、ループが完成してしまい、右下へコースが延ばせません。
したがって、下へ下がるのみ。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　‥　‥　━　‥　‥
：　：　┃　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

もう一方のコースの端に着目すると、右下へコースを延ばすためには一番下のラインを通らなければなりません。
このため通れるルートは１つのみ。


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　‥
┃　┃　┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：　┃　：　：　
　━　‥　━　‥　‥
：　┃　┃　：　：　：　
　━　‥　‥　‥　‥
┃　：　：　：　：　：　
　━　━　‥　‥　‥

２行５列の「３」の回りまで、ループができないようにコースの両端を延長してゆくと解答図に辿り着きます。
以上の考え方を採れば、４行４列と５行４列の「２」の条件は冗長になっています。

◆愛知県　Y.M.Ojisan　さんからの解答

第一関門第二関門第三関門完成

黄色０，３で示されるところの
条件から決まる経路黄色３で示される場所で
小ループにならないために
必要な経路黄色２で示される条件を満た
すのに必要な経路、
およびその結果決まる経路以後必然の経路。
唯一の解である。

第一関門	第二関門	第三関門	完成

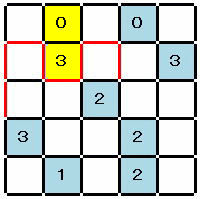
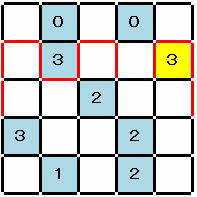
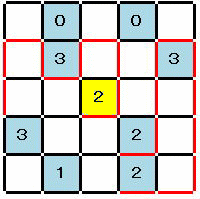
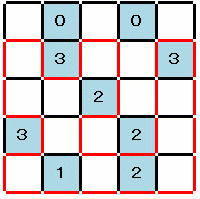
黄色０，３で示されるところの条件から決まる経路	黄色３で示される場所で小ループにならないために必要な経路	黄色２で示される条件を満たすのに必要な経路、およびその結果決まる経路	以後必然の経路。唯一の解である。

◆愛知県　ポン吉　さんからの解答


　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　━　‥　━　‥　━
┃　┃　┃　┃　┃　┃　
　‥　━　‥　‥　‥
┃　：　：　┃　┃　┃　
　━　‥　━　‥　‥
：　┃　┃　：　┃　┃　
　━　‥　━　━　‥
┃　：　：　：　：　┃　
　━　━　━　━　━

考え方：


　‥　‥　‥　‥　‥
：　：０：　：　：　：　
　‥　‥　‥　‥　‥
：　┃３┃　：　：　：　
　‥　━　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

まず、この部分から、通るべき３カ所が確定します。
次に、上の「３」の右下にある「２」に注目しますが、条件に「コースは交差しない」というのがあるため、連鎖的に確定箇所が発生します。
そのさらに右下の「２」についても同様な考え方で確定できます。


　‥　‥　‥　‥　‥
：　：０：　：　：　：　
　‥　‥　‥　‥　‥
：　┃３┃　：　：　：　
　‥　━　‥　‥　‥
：　：　：２┃　：　：　
　‥　‥　━　‥　‥
：　：　：　：２┃　：　
　‥　‥　‥　━　‥
：　：　：　：　：　：　
　‥　‥　‥　‥　‥

最初に埋めた「３」の部分からつなげようとすると、その他のヒントマスとの絡みから、以下の１通りにルートが決定できます。


　‥　‥　‥　‥　‥
：　：０：　：０：　：　
　━　‥　━　‥　‥
┃　┃３┃　┃　：　：　
　‥　━　‥　‥　‥
┃　：　：２┃　：　：　
　━　‥　━　‥　‥
：３┃　：　：２┃　：　
　━　‥　‥　━　‥
┃　：１：　：　：　：　
　━　━　━　‥　‥

中央の「２」からルートを延ばそうとすると、左に延ばすことは出来ないので、必然的に下に行くことになります。
あとは自然にルートが繋がります。

【感想】

こういう問題は初めてでしたが、ちょっと考えると簡単に解けますね。
パズル問題としては初級でしょうけど、新鮮な感覚で解けました。
もっとサイズが大きい問題をやってみたいです。

◆東京都　SHOGO　さんからの解答

まず「0」のマス周辺は通過することができない。
さらに、「0以外の数字」のマス周辺には指定数の線がなくてはならない。
これらの条件から、通過するライン、通過してはならないラインがいくつか最初にわかる。


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　‥　‥　×　
┃　：　：２：　：　┃
　‥　‥　‥　‥　‥　
：３：　：　：２：　：
　‥　‥　‥　‥　‥　
：　：１：　：２：　：
　‥　‥　‥　‥　‥

また経路は輪になるのが条件であるため、線と線が交わるそれぞれの点において線が「交差」することはありえない。
よって


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　：　×２┃　┃　┃
　‥　‥　━　×　×　
：３：　：　×２┃　┃
　‥　‥　‥　━　×　
：　：１：　×２×　┃
　‥　‥　━　━　━

ここまでを確定することが出来る。
ここで左下の「３」のマスについて考える。
上から来た線をつなげつつ、3本の線を引くには


　×　　　　　━　
┃３┃　と　×３┃
　━　　　　　━

の2パターンが考えられるが、前者を採用した場合は


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　×　×２┃　┃　┃
　‥　━　━　×　×　
┃３┃　：　×２┃　┃
　━　‥　‥　━　×　
：　：１：　×２×　┃
　‥　‥　━　━　━

の様に、図の一部で輪が終わってしまう。
よって後者で線を引いた場合は以下の通り。


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　×　×２┃　┃　┃
　━　×　━　×　×　
×３┃　┃　×２┃　┃
　━　×　‥　━　×　
：　×１：　×２×　┃
　‥　‥　━　━　━

最後に左下の「１」のマスについて考える。
この場合も右側に線を引いた場合は


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　×　×２┃　┃　┃
　━　×　━　×　×　
×３┃　┃　×２┃　┃
　━　×　×　━　×　
：　×１┃　×２×　┃
　‥　×　━　━　━

となり、輪が完成しなくなってしまうことがわかる。
よって下側に線を引いた場合


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　×　×２┃　┃　┃
　━　×　━　×　×　
×３┃　┃　×２┃　┃
　━　×　‥　━　×　
：　×１×　×２×　┃
　‥　━　━　━　━

となり、これらの線をつなぎ合わせれば輪が完成する。


　×　×　×　×　×　
×　×０×　×０×　×
　━　×　━　×　━　
┃　┃３┃　┃　┃３┃
　×　━　×　×　×　
┃　×　×２┃　┃　┃
　━　×　━　×　×　
×３┃　┃　×２┃　┃
　━　×　━　━　×　
┃　×１×　×２×　┃
　━　━　━　━　━

◆北海道の高校生　ラティウス　さんからの解答

三叉路が決して出来ないことを考慮すれば簡単でしょう。

1.左上の０と３が隣り合ってる場所は自明で、次のようなパターンになる。


○＿○＿○＿○＿○＿○
＿＿＿０＿＿＿０＿＿＿
●■●＿●■●＿○＿○
■＿■３■＿＿＿＿３＿
●＿●■●＿○＿○＿○
■＿＿＿＿２＿＿＿＿＿
●＿○＿○＿○＿○＿○
＿３＿＿＿＿＿２＿＿＿
○＿○＿○＿○＿○＿○
＿＿＿１＿＿＿２＿＿＿
○＿○＿○＿○＿○＿○

2.中央の２は上、左に線を引くと三叉路になってしまうので、右と下である。
その右下の２も同様。


○＿○＿○＿○＿○＿○
＿＿＿０＿＿＿０＿＿＿
●■●＿●■●＿○＿○
■＿■３■＿＿＿＿３＿
●＿●■●＿●＿○＿○
■＿＿＿＿２■＿＿＿＿
●＿○＿●■●＿●＿○
＿３＿＿＿＿＿２■＿＿
○＿○＿○＿●■●＿○
＿＿＿１＿＿＿２＿＿＿
○＿○＿○＿○＿○＿○

3.左の３は、上か左のどちらかを引かないので、右と下は確定。
また、右上の０の周囲に線が引けないので、１箇所線が引ける。


○＿○＿○＿○＿○＿○
＿＿＿０＿＿＿０＿＿＿
●■●＿●■●＿○＿○
■＿■３■＿■＿＿３＿
●＿●■●＿●＿○＿○
■＿＿＿＿２■＿＿＿＿
●＿●＿●■●＿●＿○
＿３■＿＿＿＿２■＿＿
●■●＿○＿●■●＿○
＿＿＿１＿＿＿２＿＿＿
○＿○＿○＿○＿○＿○

4.左下を考えてみる。
３の左を接続すると、全体が２つに分かれてしまう。
これは間違いなので、上が正解。


○＿○＿○＿○＿○＿○
＿＿＿０＿＿＿０＿＿＿
●■●＿●■●＿○＿○
■＿■３■＿■＿＿３＿
●＿●■●＿●＿○＿○
■＿＿＿＿２■＿＿＿＿
●■●＿●■●＿●＿○
＿３■＿＿＿＿２■＿＿
●■●＿○＿●■●＿○
■＿＿１＿＿＿２＿＿＿
●■●■●＿○＿○＿○

5.あとはどれをどの方向に繋げるかはほぼ自明。


○＿○＿○＿○＿○＿○
＿＿＿０＿＿＿０＿＿＿
●■●＿●■●＿●■●
■＿■３■＿■＿■３■
●＿●■●＿●＿●＿●
■＿＿＿＿２■＿■＿■
●■●＿●■●＿●＿●
＿３■＿■＿＿２■＿■
●■●＿●■●■●＿●
■＿＿１＿＿＿２＿＿■
●■●■●■●■●■●

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる

『今週の問題』第236回 解答

『今週の問題』第236回　解答