◆埼玉県 数学好きSE さんからの解答
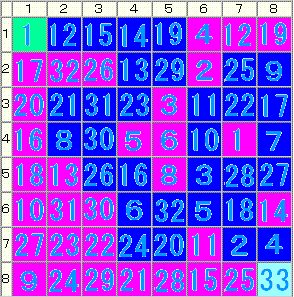
【問題1】
(1,5)→(2,5)→(2,4)→(3,4)→(3,2)→ (4,2)→(4,3)→(5,3)→(5,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(3,6)→(3,7)→ (2,7)→(2,8)→(5,8)→(5,7)→(7,7)→ (7,8)→(8,8)→【考え方】
「ちょうど33個の数字を通過する」
「同じ数字の書いてあるマス目は一度しか通過できない」
この2つの条件から、「1〜33の全ての数字を1回ずつ通過する」ことがわかるので、これを基に盤面のマス目を「通過するマス」と「通過しないマス」に分類する。
(以下、通過するマス…○ 通過しないマス…×と表記する)
問題のマス目に書かれている数字のうち、「7」と「33」は1つしかない。
(他の数字は2つずつある)
したがって、(4,8)の「7」は必ず通過するので、ここは○である。
また、スタート地点の(1,1)の「1」は当然○なので
(4,7)の「1」は×ということになる。
(同じ数字は1度しか通れない)
また、あるマスが○の場合、そのマスに隣接するマスのうち、そのマスの1手前のマスと1手後のマス(つまり、少なくとも2つ)は○でなければならない。
(ただし、スタートとゴールは例外で、隣接するマスのうち、少なくとも1つが○であればよい。)
したがって、(4,8)の「7」に隣接する、(3,8)の「17」と(5,8)の「27」は○であり、このことより(2,1)の「17」と(7,1)の「27」は ×であることがわかる。
以上の考え方を繰り返すことにより、盤面は以下のように分類できる
○○○○○××× ×□□□○×○○ ×○□○□■○○ □□□□×□×○ □□□□□□○○ □□□○□□□× ×××○○□○○ ×××××××○□■…未確定
ここで、(3,6)の「11」(図中の■)が×であると仮定すると、
(2,7)の「25」に至るには、(4,8)の「7」を通るしかなくなる。
同じマス目は2回通れないため、(2,7)の「25」のエリアに侵入すると出られなくなってしまう。
このため、(3,6)の「11」は○であり、
(7,6)の「11」は×である。
後は、先ほどと同様の議論により、盤面を以下のように完全に分類できる。
○○○○○××× ×××○○×○○ ×○○○×○○○ ×○○××○×○ ××○○×○○○ ×××○○○○× ×××○○×○○ ×××××××○上図の○を通って、スタートからゴールまで進めばよい。
【感想】
実際に紙に書いて○×をつけて考えていくと、わかりやすいですね。
難易度も高くないので、楽しく解けました。
◆新潟県の中学校3年生 si さんからの解答
まず7が一つしかないので必ず通らなくてはならない。
そしてその前後の17と27も通る必要がある。
そうするともう一つの17と27が通れなくなる。
すると27のしたの9も通れなくてもうひとつの9は通らなければならない。
それと17の右上の12は必ず通る事になる。
このようにすすめていくと
(1,5)(2,5)(2,4)(3,4)(3,3) (3,2)(4,2)(4,3)(5,3)(5,4) (6,4)(7,4)(7,5)(6,5)(6,6) (5,6)(4,6)(3,6)(3,7)(2,7) (2,8)(3,8)(4,8)(5,8)(5,7) (6,7)(7,7)(7,8)(8,8)が通らなくてはならない数になる。
(1,5)→(2,5)→(2,4)→(3,4)→(3,3)→ (3,2)→(4,2)→(4,3)→(5,3)→(5,4)→ (6,4)→(7,4)→(7,5)→(6,5)→(6,6)→ (5,6)→(4,6)→(3,6)→(3,7)→(2,7)→ (2,8)→(3,8)→(4,8)→(5,8)→(5,7)→ (6,7)→(7,7)→(7,8)→(8,8)→このようになる。
◆東京都 明 さんからの解答
(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→ (2,4)→(3,4)→(3,3)→(3,2)→(4,2)→ (4,3)→(5,3)→(5,4)→(6,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(5,6)→(4,6)→ (3,6)→(3,7)→(2,7)→(2,8)→(3,8)→ (4,8)→(5,8)→(5,7)→(6,7)→(7,7)→ (7,8)→(8,8)→【考え方】
第232回と同じ考え方で通過マスと非通過マスが決定できます。
“7”がペアを持たない通過マスとなるので、ここが起点になります。
縦、横の座標が(3,6)の“11”、(5,3)の“26”、(6,6)の“5”は通過マスとなっていますが、これは通過マスと非通過マスを決定する 過程で、非通過マスで囲まれる通過マスのブロックには出入り口が存在しなければならないことから、通過マスと決定されます。
すべての通過マスが決定されてからルートを決めますが、この問題ではルートが一通りとなっています。
◆大阪府 fuku66 さんからの解答
問題は1〜33の数字を全て踏んだ経路を探せということ。
つまり、
通れないマスを斜線を引いたり、絶対通る箇所に丸をつけたりしながら、経路を拡張させていきましょう!
以下、詳細な解答。
(部分経路とは、正解の経路の一部という意味で使っています)
スタート地点と同じ1の(4,7)は通れないので、(5,8)→(4,8)→(3,8)という部分経路が出来る。
(3,8)と同じ17が入っている(2,1)は通れないので、(1,1)→(1,2)という部分経路が出来上がる。
(5,8)と同じ27が入っている(7,1)は通れない為、(8,1)を通る経路が存在しない。
よって(8,1)以外に9が入っている(2,8)は必ず通らなければいけない。
(1,8)は通れないので、(1,5)は必ず通る。
(1,8)は通れないので、(2,7)-(2,8)-(3,8)という部分経路が出来る。
(8,7)が通れないので、(7,8)を通る
(1,5)を通るので、(1,4),(2,5)は通る
(5,7)-(5,8)を接続
(8,2)が不可なので、(7,4)を通る
(8,4),(8,6)が不可なので、(3,2),(1,3)を通る
(7,7)-(7,8)を接続
(3,7)-(2,7)を接続
(7,2)通行不可なので、(3,4)は必ず通る
(3,7)-(3,6)を接続
(7,7)-(6,7)を接続
(6,4)-(7,4)-(7,5)を接続
(7,5)-(6,5)を接続
(1,2)-(1,3)を接続
(3,3)-(3,2)-(4,2)を接続
(6,5)-(6,6)を接続
(6,1)通行不可より、(4,6)は必ず通る
(3,6)-(4,6)-(5,6)-(6,6)を接続
(6,6)-(5,6)を接続
(5,7)-(6,8)を接続
(2,4)-(2,5)を接続
(4,1)通行不可なので、(5,4)は必ず通る
(4,2)-(4,3)を接続
(4,3)-(5,3)を接続
(5,3)-(5,4)-(6,4)を接続
(1,3)-(1,4)を接続
(2,4)-(3,4)-(3,3)を接続
以上より、
(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→ (2,4)→(3,4)→(3,3)→(3,2)→(4,2)→ (4,3)→(5,3)→(5,4)→(6,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(5,6)→(4,6)→ (3,6)→(3,7)→(2,7)→(2,8)→(3,8)→ (4,8)→(5,8)→(5,7)→(6,7)→(7,7)→ (7,8)→(8,8)
(感想)
最初はルールすらわからなかったけど、面白かったです。
◆長野県の高校生 亜衣 さんからの解答
(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→ (2,4)→(3,4)→(3,3)→(3,2)→(4,2)→ (4,3)→(5,3)→(5,4)→(6,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(5,6)→(4,6)→ (3,6)→(3,7)→(2,7)→(2,8)→(3,8)→ (4,8)→(5,8)→(5,7)→(6,7)→(7,7)→ (7,8)→(8,8)
始めのマス(1,1)は【1】なので(4,7)の【1】は通らないことがわかる。
また1つしかない【7】は必ず通るので、(5,8)の【27】、(3,8)の【17】も必ず通る。
よって(7,1)の【27】と(3、8)の【17】は通らない。
このように通るところから通らないところをみつけ塗りつぶしていく。
また周りが塗りつぶされるなど、通れないことがわかったマスは、逆に同じ数字のマスは必ず通ることになる。
このように分けて(通る、通らないで2色に塗ると分かりやすいと思います)いくと道が見えてきます。
また途中行き詰ることがありますが、そのときは通るマスを仮定して塗りつぶしていくと、間違っている場合は矛盾が生じるのでわかります。
◎感想
すごくおもしろかったです。
初めは何も考えずに適当にやってたんですが、全然進めませんでした(-_-;)
1組の数字で「片方は必ず通る、もう一方は通らない」ということに気付くと、割とすぐ解けました。
◆石川県の高校生 アビュー さんからの解答
(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→ (2,4)→(3,4)→(3,3)→(3,2)→(4,2)→ (4,3)→(5,3)→(5,4)→(6,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(5,6)→(4,6)→ (3,6)→(3,7)→(2,7)→(2,8)→(3,8)→ (4,8)→(5,8)→(5,7)→(6,7)→(7,7)→ (7,8)→(8,8)→<解答の方法>
前回の数字の迷路と考え方は全く同様です。
唯一この盤面上に1つしかない「7」を通るように壁と道を決めていくだけで可能です。
このような壁と道の分別方法は前回は解説しましたが、今回はメモ程度に書いておきます。

あとはこれに従って道を進めていくと、下図のルートが分かります。
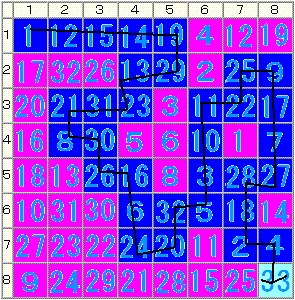
◆千葉県 DMR さんからの解答
(1,5)→(2,5)→(2,4)→(3,4)→(3,2)→ (4,2)→(4,3)→(5,3)→(5,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(3,6)→(3,7)→ (2,7)→(2,8)→(5,8)→(5,7)→(7,7)→ (7,8)→(8,8)【解説】
前回と同様の手順で解けます。
まず,全部のマスの数は,8×8=64.
64÷2=32より,盤上の数字が全てペアになっていれば,32個の数字があるはずだが,実際には,33個の数字がある。
つまり,ペアのない数字を見つけて,そこを起点として考えていけば良い。
よく探すと,ペアのない数字は,ゴールの「33(8,8)」と,「7(4,8)」だけなので,
「7(4,8)」を起点にする。
◆以下で用いる考え方◆
※ここから先は,通るべきマスを「可能マス」通らざるべきマスを「不可能マス」と呼ぶ。
あるマスを通るには,そのマスの直前のマスと,そのマスの直後のマスも通らなければならない。
したがって,可能マスには,最低でも二つの可能マスが隣り合わなければならない。
これを応用して,以下の三つの手法が使える。
例えば,隣接マスが一つしかないものは,不可能マスであるとわかる。
つまり,
?・・・未確定の数字,■・・・不可能マス,○・・・可能マスとすると,
■? ○? ■?ならば,
■? ○○ ■?となる。これを,『基本法』と呼ぶことにする。
ほかにも,
??? ■○? ■■?ならば,
?○? ■○○ ■■?と,二つの数字が可能マスと判明する。
なぜなら,この形は角でなくとも,どこでも適用できる上に,一つの数字から二つの数字の可否が判別できるからである。
これを,『角とり法』と呼ぶことにする。
あるいは,これの応用で,
??? ■?■ ?■?ならば,
??? ■■■ ?■?と,一つの数字が不可能であることがわかる。
◆ここまで◆
まず,最初に「1(1,1)」を通るので,「1(4,7)」は通らない。
したがって,「7(4,8)」に隣接するマスは「17(3,8)」「27(5,8)」の二つしかないことから,この二つは可能マス。
→「17(2,1)」は不可能マスなので,「12(1,2)」は可能マス。(基本法)
「27(7,1)」は不可能マスなので,「9(8,1)」は不可能マス。(袋小路法・応用)
→「12(1,7)」は不可能マスなので,「19(1,8)」は不可能マス。(袋小路法・応用)
「9(2,8)」は可能マスなので,「25(2,7)」は可能マス。(角とり法)
→「19(1,5)」は可能マス。
「25(8,7)」は不可能マスなので,「4(7,8)」は可能マス。(基本法)
→「4(1,6)」は不可能マスなので,「14(1,4)」と「29(2,5)」は可能マス。(角とり法)
→「14(6,8)」は不可能マスなので,「28(5,8)」「2(7,7)」は可能マス。(角とり法)
「29(8,3)」は不可能マスなので,「24(8,2)」は不可能マス。(袋小路法・応用)
→「2(2,6)」は不可能マスなので,「22(3,7)」は可能マス。(角とり法)
「24(7,4)」は可能マス。
「28(8,5)」は不可能マスなので,「21(8,4)」は不可能マス。(袋小路法・応用)
→「22(7,3)」は不可能マスなので,「23(7,2)」は不可能マス。(袋小路法)
●ここで,「22(3,7)」は,隣接する可能マスが二つあるが,「17(3,8)」●
●のマスは直前が「9(2,8)」直後が「7(4,8)」と決まっているので,●
「11(3,6)」は可能マス。
「21(3,2)」は可能マス。
「6(6,4)」「20(7,5)」は可能マス。(角とり法)
→「23(3,4)」は可能マス。
「11(7,6)」は不可能マスなので,「32(6,5)」「18(6,7)」は可能マス。(角とり法)
「15(8,6)」は不可能マス。(袋小路法)
「6(4,5)」「20(3,1)」は不可能マス。
→「15(1,3)」は可能マス。
「32(2,2)」は不可能マスなので,「8(4,2)」「31(3,3)」は可能マス。(角とり法)
「18(5,1)」は不可能マスなので,「10(6,1)」「16(4,1)」は不可能マス。(袋小路法・応用)
→「8(5,5)」は不可能マスなので,「5(6,6)」は可能マス。
(上の●ではさまれた部分と同様)
「31(6,2)」は不可能マス。
「10(4,6)」は可能マスなので,「3(5,6)」は可能マス。(基本法・応用)
「16(5,4)」は可能マス。
→「5(4,4)」は不可能マス。
「3(3,5)」は不可能マスなので,「13(2,4)」は可能マス。(角とり法)
→「13(5,2)」は不可能マスなので,「30(4,3)」は可能マス。(角とり法)
→「30(6,3)」は不可能マスなので,「26(5,3)」は可能マス。
(上の●ではさまれた部分と同様)
→「26(2,3)」は不可能マス。
こうして得られた可能マスをうまくつないでいけば,解答のようになります。
◆群馬県 天10 さんからの解答
■ルート
(1,5)→(2,5)→(2,4)→(3,4)→(3,2)→ (4,2)→(4,3)→(5,3)→(5,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(3,6)→(3,7)→ (2,7)→(2,8)→(5,8)→(5,7)→(7,7)→ (7,8)→(8,8)→■考え方
64マスに1個しかない数字は”7”と”33”の2個でした。
他の数字はみな2個づつとなっており、33個通過するためには1個使いの場所はそのまま通ることが確定、2個使いの数字の
片方の場所は通り、片方には通らないことが分かります。
問題の場合、絶対に通る7(4,8)は左が1で通ることができない場所の為、上下に必ず通ることになります。
結果、(3,8)の17と(5,8)の27は通ることが確定となります。
一方(2,1)の17と(7,1)の27は通らない場所に決まります。
その結果、(1,1)の1からは右の(1,2)の12は通ることが確定、
(8,1)の9は行止りの為、通らないことが確定
同様に通らなければいけない場所にある数字の対の場所を通らない場所と確定し、通ることができない場所の対の場所を通る場所と確定することで本問題は解くことができます。
■他のルート
本問題では不確定の場所が無かったので、他のルートは無し
◆愛媛県 レタン さんからの解答
まず、64マスに対して数字は33個で、7と33以外が2つずつあることを読み取る。
それを踏まえてこつこつと考えていく。
■■■■■□□□ □□□■■□■■ □■■■□■■■ □■■□□■□■ □□■■□■■■ □□□■■■■□ □□□■■□■■ □□□□□□□□これを通りきる方法は一通りしかありませんね。
スタート→
(1,5)→(2,5)→(2,4)→(3,4)→(3,2)→ (4,2)→(4,3)→(5,3)→(5,4)→(7,4)→ (7,5)→(6,5)→(6,6)→(3,6)→(3,7)→ (2,7)→(2,8)→(5,8)→(5,7)→(7,7)→ (7,8)→(8,8)→ゴール
理論的に「これ以外にない」で考えてきたので、他にルートはありません。
◆ 問題へもどる
◆ 今週の問題へ