
◆石川県の高校生 アビュー さんからの解答
【問題1】
START→ (2,1)→(2,2)→(3,2)→(4,2)→(5,2)→ (6,2)→(6,3)→(5,3)→(4,3)→(3,3)→ (2,3)→(2,4)→(2,5)→(3,5)→(4,5)→ (4,6)→(3,6)→(2,6)→(2,7)→(2,8)→ (3,8)→(4,8)→(5,8)→(5,7)→(6,7)→ (6,6)→(6,5)→(7,5)→(7,6)→(8,6)→ (8,7)→(8,8) →GOAL<解答の説明>
まず全体の範囲のサイズを計算します。
8×8=64ですが、ここで「33」を含まずにカウントすると合計63になります。
盤面上にある数字は33以外には1〜32しかないです。(問題の通り)
もしこの数字が互いにペアな状態であったとすれば数としては64になるはずです。
ところが実際には1〜32が書いてある盤面は63しかありません。
よって、1〜32のうちペアでない、仲間外れの数が存在するというわけです。
その仲間はずれの数はぱっと見は分かりませんが、よく見ると「5」が仲間はずれであることが分かります。
つまり「5」と最初に通る「1」をヒントに、考えていけばいいのです。
まず、「1」は何があっても間違いなく通るからもう一つの「1」は必ず通れない盤面になります。
(通れない盤面を以後「壁」と、通らなくてはいけない盤面を以後「道」として考えます)
また「5」は他にペアがないわけですから、他のところを押したとしてもここは埋まりません。
よって「5」は道となります。
すると、「5」の上下にある「12(2,8)」と「22(4,8)」は、「5」を通るためには道になる必要があります。
よって「12(2,8)」「22(4,8)」は道になるため、「12(7,8)」「22(7,1)」は壁になります。
すると、今度は出口へと行くルートが「17(8,7)」しかなくなります。
よって「17(8,7)」が道になり、伴って「17(1,8)」が壁となります。
そこから今度は「12(2,8)」から「9(2,7)」へ行くルートが1つしかなくなります。
よって「9(2,7)」も道になるから「9(7,7)」も壁になります。
その次に「17(8,7)」から抜けるルートが「4(8,6)」しかなくなり、「4(8,6)」が道になるのに伴い「4(1,7)」が壁になります。
このようにここは「道」と考えることができるから「壁」になる、という考えもあります。
しかし中には場所によっては「壁」と考えることができるから「道」になるという考えも存在します。
例えば、1番最初に言った「22(7,1)」が壁になったとき、「15(1,8)」は仮に自分自身がそこへ行ったとしても戻ってくることができません。ということは自動的にそこは壁となって、「15(6,7)」が道になるという具合の話です。
こうしてやっていくと図のように道と壁を区別できます。
(道は黄色、壁は黒)

ところが、ここまで行くとどれを壁にしたらいいか、どれを道にしたらいいか分からなくなります。
そこで、「16(7,3)が壁」を成り立つと仮定します。
もしこれが壁だったら、ちゃんとスムーズにいける道である必要があります。
ところが、それは図で示すとおり途中「25(7,5)」で壁ができるので、「32(6,5)」は壁になるはずです。
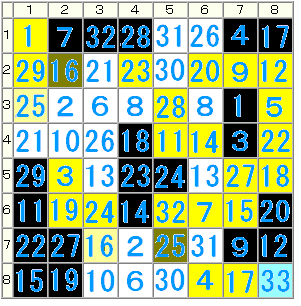
ところがすでにそこは道となっていて、矛盾が生じるために、「16(7,3)は道」という結果が得られます。
そして、最終的に壁か道かを埋めていけば、図のような領域図になるはずです。
(なお、薄い黄色が仮定した後の道で、黄土色のような謎の色(?)が仮定した後の壁だとします。)
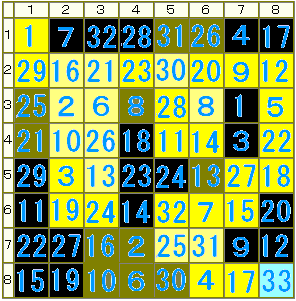
このAnswerでは、道としてたどっていくとスムーズに道として成立します。
よって、上に記したような答えがあるのです。
もしかしたら仮定する場所によってはまだ答えがあるかもしれません。
しかし、まず反転する場合は×で、それ以外の場合でもなかなか見つかりません。
◆北海道 あつし さんからの解答
【問題1】
(2,1)→(2,2)→(3,2)→(4,2)→(5,2)→ (6,2)→(6,3)→(5,3)→(4,3)→(3,3)→ (2,3)→(2,4)→(2,5)→(3,5)→(4,5)→ (4,6)→(3,6)→(2,6)→(2,7)→(2,8)→ (3,8)→(4,8)→(5,8)→(5,7)→(6,7)→ (6,6)→(6,5)→(7,5)→(7,6)→(8,6)→ (8,7)→(8,8)→で、この他に正解となるルートはありません。
考え方としては、
A:「1と33以外の通るマスは、必ず入り口と出口がある」
B:「通るマス(○)と同じ数字のマスは通らないマス(×)となる」
C:「通らないマス(×)と同じ数字のマスは通るマス(○)となる」
ということが重大なポイントとなります。
また、問題の切り口は、
D:「5のマスは1つしかないので必ず通る」
ことです。
あとは、1(左上)・5・33のマスを○、もうひとつの(5の左)1を×とすると、
Aから5の上下の12と22は○となり、
Bよりもう一方の12と22は×となります。
ここで、左下の15は、Aより○にはならないので×となります。
このことからCより、もう一方の15は○となります。
このようにABCをひたすら使いつづけていくと通るべき33マスが決定します。
それと同時にその33マスを通る道筋がただひとつに決まります。
◆東京都 明 さんからの解答
【問題1】
(2,1)→(2,2)→(3,2)→(4,2)→(5,2)→ (6,2)→(6,3)→(5,3)→(4,3)→(3,3)→ (2,3)→(2,4)→(2,5)→(3,5)→(4,5)→ (4,6)→(3,6)→(2,6)→(2,7)→(2,8)→ (3,8)→(4,8)→(5,8)→(5,7)→(6,7)→ (6,6)→(6,5)→(7,5)→(7,6)→(8,6)→ (8,7)→(8,8)→●考え方
数字を調べると、“1〜32”は“5”のみ単独で他の数字はすべてペアになっています。
33個の数字を通過し、同じ数字は2回通らないという条件から、1〜32の数字を1回ずつ通って“33”に行かなければなりません。
一筆書きの条件から任意の通過するマス(始めと終わりを除く)の隣には少なくとも2つの他の通過マスがなくてはなりません。
例
−×− −△− △○△ ×○△ ○:通過マス △:隣接する通過マス −×− −×− ×:通過しないマス −:未定マス本問では“5”が単独の通過マス、“1”は非通過マスなので隣接する“12”、“22”が通過マスでなくてはなりません。
また、ペアとなっている“12”、“22”は非通過マスとなります。
また、同じ理由で隣接するマスに少なくとも2つの通過できるマスがないときはそのマスは非通過マスとなります。
例 −×− ×△× △:新たな非通過マスまた、ペアとなる数字のマスは通過マスでなくてはなりません。
以上の性質から、本問では順に通過マス、非通過マスを決定することができ、通過ルートが単一であることが確かめられます。
【問題2】
【問題1】と同様に、“9”が単独の数字であることから順に通過マス、非通過マスを決定することができます。
(1,2)→(1,3)→(2,3)→(2,4)→(3,4)→ (3,3)→(3,2)→(3,1)→(4,1)→(4,2)→ (5,2)→(5,3)→(5,4)→(6,4)→(7,4)→ (7,5)→(6,5)→(5,5)→(4,5)→(4,6)→ (3,6)→(3,7)→(2,7)→(2,8)→(3,8)→ (4,8)→(5,8)→(5,7)→(6,7)→(7,7)→ (7,8)→(8,8)→【問題1】【問題2】とも演繹的にマスの区別ができるように数字の配置がされています。
“19”が単独のマスですが、以後演繹的な決定ができないようにしました。
01, 03, 16, 29, 09, 22, 14, 31 26, 23, 17, 04, 27, 02, 07, 25 06, 10, 30, 24, 21, 15, 04, 20 19, 01, 16, 11, 10, 28, 18, 15 32, 09, 23, 31, 06, 08, 32, 17 12, 25, 05, 18, 22, 21, 27, 07 02, 29, 12, 13, 30, 13, 14, 20 05, 24, 28, 03, 08, 11, 26, 33解が単一かは確かめていませんが、下記が解のひとつです。
○ ○ ○ ○ ○ ○ × × ○ ○ ○ ○ × ○ × × ○ ○ ○ ○ × ○ × × ○ × × ○ × ○ × × ○ × × ○ × ○ × × ○ ○ ○ ○ × ○ ○ ○ × × × × × ○ ○ ○ × × × × × × × ○
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
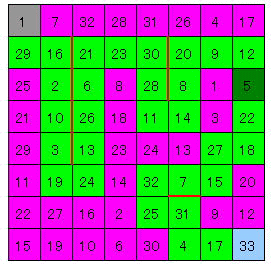
下図に示す。
5だけが一箇所しかなく、通過が確定する。
その結果、その両隣の12と22の通過が確定し、別の場所の12と22の非通過が定まる。
以後、袋小路は通過できないなどの条件で一意的に通路が定まった。
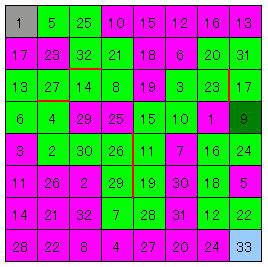
【問題2】
手法は問題1と同じ。最初の通過確定は9である。
【感想】
新体験で新鮮味があり、また実に良く考えられたパズル問題であると思いました。
解くより作るほうが大変か。
◆北海道 フェンリル さんからの解答
【問題1】
(2,1)→(2,2)→(6,2)→(6,3)→(2,3)→ (2,5)→(4,5)→(4,6)→(2,6)→(2,8)→ (5,8)→(5,7)→(6,7)→(6,5)→(7,5)→ (7,6)→(8,6)→(8,8)【問題2】
(1,1)→(2,1)→(3,1)→(3,2)→(4,2)→ (4,3)→(3,3)→(2,3)→ (1,3)→(1,4)→ (2,4)→(2,5)→(3,5)→(4,5)→(4,6)→ (4,7)→(5,7)→(5,6)→(5,5)→(5,4)→ (6,4)→(6,3)→(7,3)→(7,2)→(8,2)→ (8,3)→(8,4)→(8,5)→(7,5)→(7,6)→ (7,7)→(8,7)→(8,8)考え方
問題1の表
1 7 32 28 31 26 4 17 29 16 21 23 30 20 9 12 25 2 6 8 28 8 1 5 21 10 26 18 11 14 3 22 29 3 13 23 24 13 27 18 11 19 24 14 32 7 15 20 22 27 16 2 25 31 9 12 15 19 10 6 30 4 17 33(1)まずこの表は5と33以外は2つずつあります。
すなわち64=2×31+2となり、同じ数字は通れないのですべての数字を通らなければならないということになります。
(2)次に、(m,n)の座標を通るということは必ず出入り口が必要なので
左右上下(m+1,n)(m−1,n)(m,n+1)(m,n−1)
いずれか二つ以上の座標を通らなければなりません。
(3)(2)のことから上下左右に3つ以上通れない座標が出来たらその座標は通れません。
以上のことから実際にやってみると
スタート地点が1なので(7,3)の1は絶対通れません。
そしてその右隣の5は一個しかないので必ず通ります
そして(2)より(8,3)の5は右左が通れませんから上下12,22は必ず通ることになります
さらに対になる22を消したことによって左下角の15は右にしか通過可能座標がないので
(3)より通過不可能座標になります
すると、(1)より対になる(7,6)の15は通らなければなりません
というようにより分けていくと以下のようになります
1 29 16 21 23 30 20 9 12 2 6 28 8 5 10 26 11 14 22 3 13 27 18 19 24 32 7 15 25 31 4 17 33これが通過必須座標です。
【感想】
座標を通るには出入り口が必要っていうのがこの問題のポイントだと思います。
単独座標が1の隣にあったので割と簡単に気づけました。
もし、単独座標が角にあったらもう少し手こずったかも・・・
◆ 問題へもどる
◆ 今週の問題へ