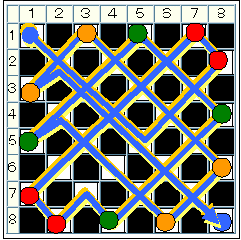
上記解答は下図の構造を持つことが分かる。
◆東京都の高校生 もやし さんからの解答
【おまけ】
今年の1月1日は日曜日。
365÷7=52…1から、来年の1月1日は月曜日。
よって、閏年を考えなければ今年と同じカレンダーを使えるのは7年後の2013年。
しかし、閏年の翌年の1月1日の曜日は2つずれる。
1月1日が火曜日の2008年は閏年だから、2009年の1月1日は木曜日。
日曜日は木曜日の3日後だから、次に1月1日が日曜日になるのは2009年の3年後である2012年。
でも、2012年は閏年だから今年と同じカレンダーは使えない。
2012年の次に1月1日が日曜日になるのは、上と同じように考えると、2012年と2016年が閏年であることから、2017年。
∴2017年
ちなみにその次は2023年。
◆広島県 清川 育男 さんからの解答
【おまけ】
2017 年
2023 年
2034 年
2045 年
2051 年
2062 年
2073 年
2079 年
2090 年
◆東京都 明 さんからの解答
【問題1】
(8,8)の石を最後に拾う場合。
スタート(1,1)→
(3,3)→(1,5)→(4,8)→(8,4)→(5,1)→
(4,2)→(3,1)→(1,3)→(6,8)→(8,6)→
(6,4)→(8,2)→(7,1)→(1,7)→(2,8)→
(5,5)→(8,8)→
(8,8)の石を先に拾う場合。
スタート(1,1)→
(8,8)→(3,3)→(1,5)→(4,8)→(8,4)→
(5,1)→(4,2)→(3,1)→(1,3)→(6,8)→
(8,6)→(6,4)→(2,8)→(1,7)→(7,1)→
(8,2)→
【問題2】
最短手数は16手になります。
理由
石を拾う時に、拾う方向を変える位置を転向点と呼ぶことにします。
石を拾う手数は、転向点の数に最後に拾う石を加えた数になります。
マス目の最外周にある石は転向点、もしくは最後の石となります。
したがって最短の手数は13手以上になります。
最外周の石だけを転向点としてとれる石を1つのグループとして、グループ分けをすると、以下の4つに分かれます。
(1,1)−(8,8)
(1,3)−(6,8)−(8,6)−(3,1)
(1,5)−(4,8)−(8,4)−(5,1)
(1,7)−(2,8)−(8,2)−(7,1)
グループ間を移動するためには少なくとも1つの転向点が必要になります。
したがって、すべてのグループを移動するためには最小で3つの余分な転向点が必要になります。
以上により最短手数は16手以上となり、実際16手で取り切る手順が存在します。
なお、(8,8)を最後に拾う場合は、最初に取り番が(1,1)−(8,8)のグループにあるため、さらに移動のための転向点が最初に1つ必要になり、最短手数は
17手になります。
取り方の数について、手計算で求めました。
(すべてを挙げ尽くしているか心配ですが)
16手で取り切る場合、(8,8)の石をとってから、他のグループの石を取ることになります。
最初の転向点の候補・・・6
次に取る端の石の候補・・・2
グループ内の端の石の取り方(右回り、左回り)・・・2
次の転向点の候補・・・4
次に取る端の石の候補・・・2
グループ内の端の石の取り方・・・2
次の転向点の候補・・・2
次に取る端の石の候補・・・2
グループ内の端の石の取り方・・・2
以上で場合の数は
6×2×2×4×2×2×2×2×2=3072
これから石が取りきれない場合の数を除きます。
取りきれない場合のルートを、図を書いて求めてみました。
図の対称性から、それぞれ(2,4)、(2,6)、(3,5)の石が残る場合の数を数えました。
指定した石を通らないような取り方は次のようになりました。
(2,4)を残す場合
8通りで、取り始めの石が2箇所
8通りで、取り始めの石が1箇所
(2,6)を残す場合
16通りで、取り始めの石が1箇所
(3,5)を残す場合
4通りで、取り始めの石が2箇所
4通りで、取り始めの石が1箇所
残る石を指定して石取りのルートを決めると、他に残る石は存在せず、したがって、2重にカウントはされません。
以上から、石が残る場合の数は52通り。
対称性から全体で石の残る場合の数は208通り。
以上から16手で取り切る場合の数は
3072−208=2864通りと求まりました。
【おまけ】
曜日と月日が一致する年を求めます。
閏年が4年ごとにあり、この4年間に曜日は5日分ずれます。
曜日のずれが7の倍数になれば曜日と月日が一致することになります。
2100年未満で条件に合う年を求めます。
n≧0 の整数とし、
4n 年後 曜日のずれは 5n 日
4n+1年後 曜日のずれは 5n+1日
4n+2年後 曜日のずれは 5n+2日 (閏年)
4n+3年後 曜日のずれは 5n+4日
閏年を除く年で曜日のずれが7の倍数になる年が求める年です。
5nが7の倍数の場合、n=7k
したがって28k年後。
5n+1が7の倍数の場合、n=4+7k
したがって17+28k年後。
5n+4が7の倍数の場合、n=2+7k
したがって、11+28k年後。
(ただしk≧0 の整数)
本年以後で曜日と月日が一致する一番近い年は11年後の2017年です。
(もっとも曜日を書き換えれば今年のカレンダーを来年使うこともできますが)
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
17回の手を下図に示す。

上記解答は下図の構造を持つことが分かる。

【問題2】
最短 16手
例えば:
(1,1)→(8,8)→(7,7)→(6,8)→(1,3)→
(3,1)→(8,6)→(7,5)→(8,4)→(5,1)→
(1,5)→(4,8)→(3,7)→(2,8)→(1,7)→
(7,1)→(8,2)
PC探索により 2864通り
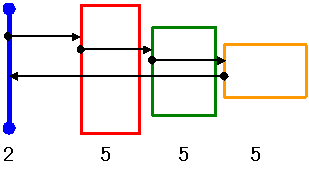
∵ 問題1で見つけた手順を検討すると、下図に示すようにさらに一手削減可能であることが分かる。
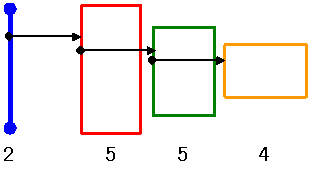
赤 緑 黄色のグループの順列は6通り、
グループ間の移動の入り口ポイントは2箇所あり、
グループ内の移動は初期方向×回転方向の4通りが考えられ、最大でも3072通りである。
実際にPCでチェックすると 2864通りであった。
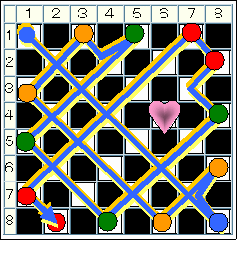
因みに、3072通りからから除外されるのは下記のようなケースである。
16手までではハートマークのところが残る。
◆ 問題へもどる
◆ 今週の問題へ