『今週の問題』第225回　解答

◆静岡県の高校生　Feather　さんからの解答

【問題１−１】

とりあえず４つ見つけました

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,2)→(7,2)→
(7,5)→(1,5)→(4,8)→(4,6)→

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,2)→(8,2)→
(4,6)→(4,7)→(2,5)→(7,5)→

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,5)→(7,5)→
(7,2)→(1,2)→(4,5)→(4,8)→

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,5)→(7,5)→
(4,8)→(4,5)→(1,2)→(8,2)→
【問題２】

繰り下げの関係から最初に次の通り 


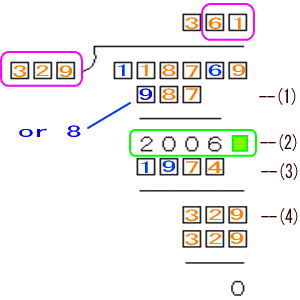
　　　　　　　　　　　　□□□ーＡＢＣとする
　　　　　　　　＿＿＿＿＿＿＿
Ｘとするー□□□）１１□□６□ーＹとする
　　　　　　　　　　９□□
　　　　　　　　　　――――
　　　　　　　　　　２００６
　　　　　　　　　　１９□□
　　　　　　　　　　――――
　　　　　　　　　　　　□□□
　　　　　　　　　　　　□□□
　　　　　　　　　　　　―――
　　　　　　　　　　　　　　０
Ｘ＊Ａ＝９□□
Ｘ＊Ｂ＝１９□□
Ｘ＊Ｃ＝□□□
よりＢ＝２＊Ａ
Ｃ≦Ａ

（Ａ，Ｂ）＝（１，２）（２，４）（３，６）（４，８）

ここまで紙上で計算しましたがギブアップで、残り１９９通りをエクセル関数で計算しました。
方法は９≧Ｙ−Ｘ＊Ａ＊１０≧０となるＣを捜しました

結果…Ｘ＝３２９　ＡＢＣ＝３６１ 

　　　　　　　３６１
　　　＿＿＿＿＿＿＿
３２９）１１８７６９
　　　　　９８７
　　　　　――――
　　　　　２００６
　　　　　１９７４
　　　　　――――
　　　　　　　３２９
　　　　　　　３２９
　　　　　　　―――
　　　　　　　　　０

◆滋賀県の高校生　-25-@ucchie　さんからの解答

【問題２】

答え:『118769÷329＝361』

[考え方]

虫食い算の
『2006-□□□□=□□』の□に当てはまる1桁の数字を順にa,b,c,d,e,fとし，
その次の計算
『□□□-□□□=0』⇔『ef□-ef□=0』の□に当てはまる1桁の数字をgとする。

======================================

まず、
　 2006-abcd=ef…(1)
の部分に注目します。

ここで、割る数をN(3桁の自然数)とします。

abcdはNの倍数なので、(1)を満たすためのNの条件はまず

1907≦kN≦1996(k=2,3,4,…,9)…(2)

が成り立たなければいけません。

(2)にk=2,3,…,9を代入して整理すると、

=======================================

(k):(Nの範囲);(efの値)

2:954~998;(98~10)
3:636~665;(98~11)
4:477~499;(98~10)
5:382~399;(96~11)
6:318~332;(98~14)
7:273~285;(95~11)
8:239~249;(94~14)
9:212~221;(98~17)

=======================================

ここで，efgの値はNの範囲からして，

efg=lN(l=1,2,3,4)を満たす必要がある。

以下、k=2,…,9の時のNの値とそれに対応するefgの値を示す。

・k=2:

(N,efg)
=(954,98g)
,(955,96g)
,(956,94g)
,…

・k=3:

(N,efg)
=(636,98g)
,(637,95g)
,…
,(647,65g)
,(648,62g)
,…

・k=4:

(N,efg)
=(477,98g)
,(478,94g)
,…
,(489,50g)
,(488,46g)
,…

・k=5:

(N,efg)
=(382,96g)
,(383,91g)
,…
,(385,81g)
,(386,76g)
,…
,(393,41g)
,(394,36g)
,…

・k=6:

(N,efg)
=(318,98)
,(319,92)
,…
,(323,68g)
,(324,62g)
,…
,(328,38g)
,(329,32g)(条件を満たせる)
,…

・k=7

(N,efg)
=(273,95g)
,(274,88g)
,(275,81g)
,(276,74g)
,(277,67g)
,(278,60g)
,(279,53g)
,…
,(282,32g)
,(283,25g)
,…

・k=8

(N,efg)
=(239,94g)
,(240,86g)
,(241,78g)
,(242,70g)
,(243,62g)
,(244,54g)
,(245,46g)
,(246,38g)
,(247,30g)
,(248,22g)
,(249,14g)


・k=9

(N,efg)
=(212,98g)
,(213,89g)
,(214,80g)
,(215,71g)
,(216,62g)
,(217,53g)
,(218,44g)
,(219,35g)
,(220,26g)
,(221,17g)

以上から条件を満たせるのは、
k=6,N=329でこのときg=9とすればよい。

ここで、
『□□□□-□□□=200』の部分を満たすことが出来るかを考える.

上の□□□は329の倍数で、かつ,800≦□□□≦999より,
329*3=987だけが条件を満たせる。

このとき，□□□□=1187と定めることができ，商も3桁の数字であるから全ての条件を満たすことができる。

以上から、
『118769÷329=361』
だけがこの問題の答えである。

◆滋賀県　松尾　さんからの解答

【問題１−１】

他にもっとあると思いますが、以下の３通りが見つかりました。 

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,2)→(7,2)→
(7,5)→(2,5)→(4,7)→(4,6)→

スタート(1,1)→
(8,1)→(8,8)→(1,8)→(1,2)→(7,2)→
(7,5)→(2,5)→(4,5)→(4,7)→

スタート(1,1)→
(8,1)→(8,8)→(2,8)→(8,2)→(1,2)→
(1,7)→(7,7)→(7,5)→(2,5)→
【問題２】

４行目の２００６から下のマスを埋めてみます。
下図のように一部の□をa、b、c、dとすると、以下の式が成り立ちます。

（２００６−（d×a））×１０＋c＝d×b
　　２００６−（d×a）＝（d×b−c）÷１０
　　２００６＝（d×b−c）÷１０＋d×a
　　２００６＝d×（b÷１０−c÷１０÷d＋a）
　　２００６÷（b÷１０＋a−c÷１０÷d）＝d

ここで　c÷１０÷d　は十分に小さい数なので、上の式は

　　２００６÷（b÷１０＋a）＝d−h　―――　式１

と表せます。
（hは十分に小さい正の数です。） 


　　　　　　　　□a b　＜―――　１行目
　　　　―――――――
　　d　）□□□□□ c　＜―――　２行目
　　　　 　 □□□□　　＜―――　３行目
　　　　　――――――
　　　　　 ２００６　　＜―――　４行目
　　　　　 □□□□　　＜―――　５行目
　　　　　　―――――
　　　　　　　 □□ c　＜―――　６行目
　　　　　　　 □□□　＜―――　７行目
　　　　　　　 ―――
　　　　　　　 　　 0　＜―――　８行目
aは２〜９です。
なぜなら、５行目は４桁なので、０、１では足りません。

bは０〜９です。
したがって、式１の左辺の　　b÷１０＋a　は　
2.0、2.1、・・・、3.0、3.1、・・・、・・・、9.0、9.1、・・・　となります。

また、５行目は1907〜1996です。
2006−(５行目)＝２桁になるからです。

まず、b÷１０＋aが2.0、2.1、・・・となる場合を検討します。
　2006÷2.0＝1003、d＝1004、４桁になるので、不可。

　2006÷2.1＝955.2、d＝956、2006−956×2＝94、940＋cは956にならないので、不可。
（なぜならcは０〜９）

２００６÷2.2＝911.8、d＝912、912×2＝1824で1907に足りないので、不可。

　以下、2.3〜2.9も1907に足りず、不可です。

これを、3.0〜、4.0〜、・・・と確認します。
まとめると以下のようになります。 
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
　　　　　0.0　　0.1　　0.2　　0.3　　0.4　　0.5
――――――――――――――――――――――――――
　２　　　1004　956　　(912)
　３　　　669　　648　　(627)
　４　　　502　　490　　478　(467)
　５　　　402　　394　　386　(379)
　６　　　335　　329　　324　(319)
　７　　　287　　283　　279　274　(272)
　８　　　251　　248　　245　242　239　(236)
　９　　　223　　221　　219　216　214　(212)
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
右の括弧内は1907に足りなくなる数字です。
ここから右にいっても同じです。

上のすべての数値をチェックすると6.1の329だけ式が成立します。
d＝329で2006より全ての□を埋めてみると下のように埋まりました。 

　　　　　　　　３６１
　　　　―――――――
　329　）１１８７６９
　　　　　　９８７
　　　　　――――――
　　　　　　２００６
　　　　　　１９７４
　　　　　　　　―――
　　　　　　　　３２９
　　　　　　　　３２９
　　　　　　　　―――
　　　　　　　　　　 0

◆広島県　清川　育男　さんからの解答

【問題１−１】

９手

スタート(1,1)→
(4,1)→(4,8)→(1,5)→(7,5)→(7,2)→
(1,2)→(1,8)→(8,8)→(8,1)→

【問題１−２】

１０２通り。


NO.    1
 A( 4 , 1 ) A( 4 , 7 ) A( 2 , 5 ) A( 7 , 5 ) A( 7 , 2 )
 A( 1 , 2 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 1 )

NO.    2
 A( 4 , 1 ) A( 4 , 7 ) A( 2 , 5 ) A( 8 , 5 ) A( 8 , 2 )
 A( 1 , 2 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 1 )

NO.    3
 A( 4 , 1 ) A( 4 , 8 ) A( 1 , 5 ) A( 7 , 5 ) A( 7 , 2 )
 A( 1 , 2 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 1 )

NO.    4
 A( 4 , 1 ) A( 4 , 8 ) A( 1 , 5 ) A( 8 , 5 ) A( 8 , 2 )
 A( 1 , 2 ) A( 1 , 8 ) A( 8 , 8 ) A( 8 , 1 )

NO.    5
 A( 4 , 1 ) A( 4 , 8 ) A( 7 , 5 ) A( 1 , 5 ) A( 1 , 8 )
 A( 8 , 8 ) A( 8 , 1 ) A( 7 , 2 ) A( 1 , 2 )

NO.    6
 A( 8 , 1 ) A( 8 , 5 ) A( 1 , 5 ) A( 1 , 8 ) A( 8 , 8 )
 A( 8 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 7 )

NO.    7
 A( 8 , 1 ) A( 8 , 5 ) A( 1 , 5 ) A( 1 , 8 ) A( 8 , 8 )
 A( 8 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 8 )

NO.    8
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 7 , 8 ) A( 7 , 5 ) A( 2 , 5 )

NO.    9
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 7 , 8 ) A( 7 , 5 ) A( 1 , 5 )

NO.   10
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 8 , 8 ) A( 8 , 5 ) A( 2 , 5 )

NO.   11
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 8 , 8 ) A( 8 , 5 ) A( 1 , 5 )

NO.   12
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 7 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )

NO.   13
 A( 8 , 1 ) A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )
 A( 7 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 8 , 5 )

NO.   14
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 5 ) A( 7 , 5 )
 A( 7 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )

NO.   15
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 5 ) A( 8 , 5 )
 A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )

NO.   16
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 7 , 8 ) A( 7 , 5 ) A( 2 , 5 )

NO.   17
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 7 , 8 ) A( 7 , 5 ) A( 1 , 5 )

NO.   18
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 8 , 8 ) A( 8 , 5 ) A( 2 , 5 )

NO.   19
 A( 8 , 1 ) A( 8 , 7 ) A( 1 , 7 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 8 , 8 ) A( 8 , 5 ) A( 1 , 5 )

NO.   20
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 4 , 7 ) A( 2 , 5 ) A( 7 , 5 )

NO.   21
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 4 , 7 ) A( 2 , 5 ) A( 8 , 5 )

NO.   22
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 5 , 7 ) A( 7 , 5 ) A( 2 , 5 )

NO.   23
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 5 , 7 ) A( 7 , 5 ) A( 1 , 5 )

NO.   24
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 6 , 7 ) A( 8 , 5 ) A( 2 , 5 )

NO.   25
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 6 , 7 ) A( 8 , 5 ) A( 1 , 5 )

NO.   26
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 7 , 7 ) A( 7 , 5 ) A( 2 , 5 )

NO.   27
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 7 , 7 ) A( 7 , 5 ) A( 1 , 5 )

NO.   28
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 8 , 7 ) A( 8 , 5 ) A( 2 , 5 )

NO.   29
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 7 ) A( 8 , 7 ) A( 8 , 5 ) A( 1 , 5 )

NO.   30
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 5 , 8 ) A( 2 , 5 ) A( 7 , 5 )

NO.   31
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 1 , 8 ) A( 5 , 8 ) A( 2 , 5 ) A( 8 , 5 )

NO.   32
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 6 , 7 ) A( 1 , 7 ) A( 1 , 5 ) A( 7 , 5 )

NO.   33
 A( 8 , 1 ) A( 8 , 8 ) A( 2 , 8 ) A( 8 , 2 ) A( 1 , 2 )
 A( 6 , 7 ) A( 1 , 7 ) A( 1 , 5 ) A( 8 , 5 )

NO.   34
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 7 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 7 )

NO.   35
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 7 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 8 )

NO.   36
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 7 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )

NO.   37
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 5 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )

NO.   38
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 4 , 8 ) A( 4 , 6 ) A( 8 , 2 ) A( 1 , 2 )

NO.   39
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 4 , 8 ) A( 4 , 5 ) A( 1 , 2 ) A( 7 , 2 )

NO.   40
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 4 , 8 ) A( 4 , 5 ) A( 1 , 2 ) A( 8 , 2 )

NO.   41
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 7 , 5 )
 A( 4 , 8 ) A( 4 , 5 ) A( 7 , 2 ) A( 1 , 2 )

NO.   42
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 8 , 5 )
 A( 8 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 7 )

NO.   43
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 8 , 5 )
 A( 8 , 2 ) A( 1 , 2 ) A( 4 , 5 ) A( 4 , 8 )

NO.   44
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 8 , 5 )
 A( 8 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )

NO.   45
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 5 ) A( 8 , 5 )
 A( 6 , 7 ) A( 3 , 7 ) A( 8 , 2 ) A( 1 , 2 )

NO.   46
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 6 )

NO.   47
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 5 )

NO.   48
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 4 )

NO.   49
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 3 )

NO.   50
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 2 )

NO.   51
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 1 )

NO.   52
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 3 ) A( 4 , 7 )

NO.   53
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 2 , 5 ) A( 4 , 3 ) A( 4 , 8 )

NO.   54
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 6 )

NO.   55
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 5 )

NO.   56
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 4 )

NO.   57
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 3 )

NO.   58
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 2 )

NO.   59
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 1 )

NO.   60
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 2 ) A( 4 , 7 )

NO.   61
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 7 , 5 ) A( 1 , 5 ) A( 4 , 2 ) A( 4 , 8 )

NO.   62
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 7 ) A( 2 , 5 ) A( 7 , 5 )

NO.   63
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 7 ) A( 2 , 5 ) A( 8 , 5 )

NO.   64
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 8 ) A( 1 , 5 ) A( 7 , 5 )

NO.   65
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 8 ) A( 1 , 5 ) A( 8 , 5 )

NO.   66
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 8 ) A( 7 , 5 ) A( 2 , 5 )

NO.   67
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 7 , 2 )
 A( 4 , 5 ) A( 4 , 8 ) A( 7 , 5 ) A( 1 , 5 )

NO.   68
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 6 )

NO.   69
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 5 )

NO.   70
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 4 )

NO.   71
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 3 )

NO.   72
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 2 )

NO.   73
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 7 ) A( 4 , 1 )

NO.   74
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 3 ) A( 4 , 7 )

NO.   75
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 2 , 5 ) A( 4 , 3 ) A( 4 , 8 )

NO.   76
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 6 )

NO.   77
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 5 )

NO.   78
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 4 )

NO.   79
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 3 )

NO.   80
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 2 )

NO.   81
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 8 ) A( 4 , 1 )

NO.   82
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 2 ) A( 4 , 7 )

NO.   83
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 8 , 5 ) A( 1 , 5 ) A( 4 , 2 ) A( 4 , 8 )

NO.   84
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 7 ) A( 2 , 5 ) A( 7 , 5 )

NO.   85
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 7 ) A( 2 , 5 ) A( 8 , 5 )

NO.   86
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 8 ) A( 1 , 5 ) A( 7 , 5 )

NO.   87
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 8 ) A( 1 , 5 ) A( 8 , 5 )

NO.   88
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 8 ) A( 7 , 5 ) A( 2 , 5 )

NO.   89
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 4 , 6 ) A( 4 , 8 ) A( 7 , 5 ) A( 1 , 5 )

NO.   90
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 4 , 7 ) A( 2 , 5 ) A( 7 , 5 )

NO.   91
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 4 , 7 ) A( 2 , 5 ) A( 8 , 5 )

NO.   92
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 5 , 7 ) A( 7 , 5 ) A( 2 , 5 )

NO.   93
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 5 , 7 ) A( 7 , 5 ) A( 1 , 5 )

NO.   94
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 6 , 7 ) A( 8 , 5 ) A( 2 , 5 )

NO.   95
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 6 , 7 ) A( 8 , 5 ) A( 1 , 5 )

NO.   96
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 7 , 7 ) A( 7 , 5 ) A( 2 , 5 )

NO.   97
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 7 , 7 ) A( 7 , 5 ) A( 1 , 5 )

NO.   98
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 8 , 7 ) A( 8 , 5 ) A( 2 , 5 )

NO.   99
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 3 , 7 ) A( 8 , 7 ) A( 8 , 5 ) A( 1 , 5 )

NO.  100
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 5 , 8 ) A( 2 , 5 ) A( 7 , 5 )

NO.  101
 A( 8 , 1 ) A( 8 , 8 ) A( 1 , 8 ) A( 1 , 2 ) A( 8 , 2 )
 A( 2 , 8 ) A( 5 , 8 ) A( 2 , 5 ) A( 8 , 5 )

NO.  102
 A( 8 , 1 ) A( 4 , 5 ) A( 4 , 8 ) A( 7 , 5 ) A( 1 , 5 )
 A( 1 , 8 ) A( 8 , 8 ) A( 8 , 2 ) A( 1 , 2 )
【問題２】

               361
         --------
    329)118769
           887
          -----
           2006
           1974
          ------
              329
              329
             ----
                 0

◆愛知県　Y.M.Ojisan　さんからの解答

【問題１−１】　９手

スタート(1,1)→(8,1)→(8,8)→(1,8)→(1,2)→(7,2)→(7,5)→(2,5)→(4,7)→(4,6)→

【問題１−２】　７０通り

　第２２３回のプログラムで探索した。
　　

【問題２】

考え方

  1. （２）−（３）が２桁落ちていることから（３）の上２桁は１９である。

  2. （２）の値から（１）の段は８００〜９９９である。

  3. 以上の値は除数（３桁）×１桁でなければならず、これより除数は下記の範囲である。
    ２１１〜２２２、２３８〜２４９、３１７〜３３３、４７５〜４９９、９５０〜９９９

  4. （２）の段から　２００６０〜２００６９＝除数（３桁）×２桁　でなければならない。

  5. ２００６０〜２００６９をそれぞれ素因数分解し、３桁×２桁となるものをリストアップする。

  6. そのれらの中で３桁の方の数値が３．に示した範囲にあるものは　
    ２００６９＝３２９×６１のみである。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる