 悢妛偺晹壆傊傕偳傞
悢妛偺晹壆傊傕偳傞仧嶉嬍導偺拞妛峑俁擭惗丂崟廫帤丂偝傫偐傜偺夝摎
嵍忋偐傜塃偵(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)偲偡傞丅
昞傪尒偰(3)偵偼俀偐俁偟偐擖傜側偄丅
乮侾偩偲廲偺寁嶼偑弌棃側偄丄係埲忋偱傕廲偺寁嶼偑弌棃側偄乯
傑偢(3)傪俀偲峫偊傞偲丄(8)偵偼俀偑擖傞丅
(1)傪俇偲偡傞偲乮侾丄俁丄俆丄俈偼婏悢偩偐傜晄壜擻丅俀丄係偼(3)傪俀偵弌棃側偄乯
(2)偑侾偵側傞丅
偦偆偡傞偲丄(7)偵偼侾乣俆偑擖傞偑丄慡偰(4)偺晹暘偱偍偐偟偔側傞丅
(1)傪俉偲偡傞偲丄(2)偑俀偵側傞丅
偦偆偡傞偲丄(7)偵偼侾偟偐擖傜側偔側傞偑丄偙傟傕寁嶼偟偰偄偔偲(4)偱偍偐偟偔側傞
師偵(3)傪俁偱峫偊傞偲丄(8)偵偼俈偑擖傞丂
(3)仺俁丂(8)仺俈
偦偆偡傞偲丄(1)偵偼俉偟偐擖傜側偔側傝丂(1)仺俉
(2)偵偼侾偑擖傞丅
(2)仺侾
(4)丄(7)偺偳偪傜偐傜峫偊偰傕偄偄偑丄
(4)偼侾乣係偑擖傝丄(7)偵偼侾乣俆偑擖傞
(4)偺曽偑妝偦偆偩偐傜丄(4)偐傜峫偊偰偄偔偲
(4)傪侾偱寁嶼偟偰偄偔偲丄(7)偑偍偐偟偔側傞丅
(4)傪俀偱寁嶼偟偰偄偔偲慡偰偺幃偑惉棫偡傞丂
(4)仺俀丂(5)仺俈丂(6)仺俇丂(7)仺俁丂(10)仺俈丂(9)仺係
偩偐傜(1)仺俉
(2)仺侾
(3)仺俁
(4)仺俀
(5)仺俈
(6)仺俇
(7)仺俁
(8)仺俈
(9)仺係
(10)仺俈
仧惷壀導偺崅峑惗丂Feather丂偝傫偐傜偺夝摎
俉亐俀亅侾亖俁 俀亄俈亅係亖俆 係亄俇亅俁亖俈 係亅俁亄俈亖俉 俉亊俀亐係亖係 俀亄俈亅俇亖俁 侾亊係亄俁亖俈 俁亊俆亄俈亖俉亙愢柧丠亜
丂丂偁丂丂丂偄丂丂丂偆丂丂丂偊 丂劇劅劍劅劍劅劍劅劍劅劍劅劍劅劉 偐劆俙劆亐劆俀劆亅劆俛劆亖劆俠劆偐丗俙乕俀俛亖俀俠 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 丂劆亊劆仭劆亄劆仭劆亊劆仭劆亊劆 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 偒劆俢劆亄劆俤劆亅劆係劆亖劆俆劆偒丗俢亄俤亖俋 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 丂劆亐劆仭劆亅劆仭劆亄劆仭劆亅劆 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 偔劆係劆亄劆俥劆亅劆俧劆亖劆俫劆偔丗係亄俥亖俧亄俫 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 丂劆亖劆仭劆亖劆仭劆亖劆仭劆亖劆 丂劌劅劑劅劑劅劑劅劑劅劑劅劑劅劎 偗劆俬劆亅劆俁劆亄劆俰劆亖劆俉劆偗丗俬亄俰亖侾侾 丂劋劅劏劅劏劅劏劅劏劅劏劅劏劅劊仠偁丗俙俢亖係俬
嵟弶偵
俙乣俰偼堦寘偺帺慠悢
俙丗嬼悢
俛丗侾丆俀
俠丗俀丆俁
俢丗俙亖俀丆俇偺帪嬼悢
俤丗亗侾
俥丗亗俋
俧丗亝俆
俫丗俀丆俈
俬丗亗侾
俰丗亞俆
俙亖俀丆係丆俇丆俉
俠亖俀丆俁偐傜
俙亖俀偺帪仺俛偑惉傝棫偨側偄亊
俙亖係偺帪仺俛亖俠亖侾丂亊
俙亖俇偺帪仺俛亖侾丄俠亖俀
俙亖俉偺帪仺乮俛丆俠乯亖乮侾丆俁乯乮俀丆俀乯
傛偭偰俙亖俇丆俉
乮俬丆俰乯亖乮俇丆俆乯乮俆丆俇乯乮係丆俈乯乮俁丆俉乯乮俀丆俋乯
俙亖俇丆俉
俢亗侾丆俉丆俋
偐傜
俙俢亖俀係丆侾俇丆侾俀
俢亖俀丆俁丆係
傛偭偰
俤亖俆丆俇丆俈
俥亖係丆俆丆俇
偔丗俧亖係亄俥亅俫
俧亖係亄乮係丆俆丆俇乯亅乮俀丆俈乯
俧亖侾丆俀丆俁丆俇丆俈丆俉
俧亝俆傛傝
俧亖侾丆俀丆俁
傛偭偰
俫亖俈丂俠亖俁
偐丗俙亅俀俛亖俇
傛傝丂俙亖俉丄俛亖侾
丂偔丂丗俥亅俧亖俁
丂偆丂丗俰亅俧亖係
偆亅偔丗俰亅俥亖侾
傛傝
俰亖俆丆俇丆俈
俬亖係丆俆丆俇
俀俢亖乮係丆俇丆俉乯
俬亖乮係丆俆丆俇乯
傛傝
俬亖乮係丆俇乯丂俢亖乮俀丆俁乯
俢亖俁偲壖掕偡傞偲
偒丗俁亄俤亖俋丂丂丂乧俤亖俇
偄丗俀亄俇亅俥亖俁丂乧俥亖俆
偔丗係亄俆亖俧亄俈丂乧俧亖俀
偆丗侾亊係亄俀亖俰丂乧俰亖俇
偗丗俬亅俁亄俇亖俉丂乧俬亖俆
偙偺偲偒丂俬亖乮係丆俇乯偵柕弬偡傞偺偱
俢亖俁偼揔偝側偄
俢亖俀偲壖掕偡傞
偒丗俀亄俤亖俋丂丂丂乧俤亖俈
偄丗俀亄俈亅俥亖俁丂乧俥亖俇
偔丗係亄俇亖俧亄俈丂乧俧亖俁
偆丗侾亊係亄俁亖俰丂乧俰亖俈
偗丗俬亅俁亄俈亖俉丂乧俬亖係
傛偭偰惉傝棫偮
仧惷壀導丂medaka丂偝傫偐傜偺夝摎
亂摎偊亃
俉亐俀亅侾亖俁
俀亄俈亅係亖俆
係亄俇亅俁亖俈
係亅俁亄俈亖俉
俉亊俀亐係亖係
俀亄俈亅俇亖俁
侾亊係亄俁亖俈
俁亊俆亅俈亖俉
亂夝朄亃
丠偺晹暘偵曄悢倎丆倐丆..., 倞傪弴偵妱傝摉偰傞偲埲壓偺幃偑摼傜傟傞丅
乮俙丆俢偵傛傞彂偒姺偊乯
a / 2 - b = c ... (1) 仺 A - b = c丂丂... (1)仈
d + e - 4 = 5 ... (2) 仺 2D + e = 9丂丂... (2)仈
4 + f - g = h ... (3)
i - 3 + j = 8 ... (4)
a * d / 4 = i ... (5) 仺 A D = i丂 丂丂... (5)仈
2 + e - f = 3 ... (6)
b * 4 + g = j ... (7)
c * 5 - h = 8 ... (8)
偨偩偟丄倎乣倞偼丄偦傟偧傟侾乣俋偺惍悢偲偡傞丅
(1)丆(5)偑惍悢夝傪帩偮偨傔偵偼丄倎丆倓偼嬼悢偱側偗傟偽側傜側偄丅
傛偭偰丄曄悢俙丆俢傪埲壓偺幃偵傛傝摫擖偡傞丅
a = 2 * A ... (9)
d = 2 * D ... (10)
倎丆倓偼丄侾乣俋偺惍悢偱偁傞偐傜丄俙丆俢偼侾乣係偺惍悢偵惂尷偝傟傞丅
(3)丆(8)傛傝丄
丂倖亅倗亖俆們亅侾俀丂...丂(11)
(4)丆(7)傛傝丄
丂倝丂亄係倐亄倗丂亖侾侾丂丂丂丂...丂(12)
(2)仈丆(6)傛傝丄
丂俀俢亄倖亖俉丂丂丂丂丂...丂(13)
(11)丆(12)傛傝丄
丂倝丂亄係倐亄倖丂亖俆們亅侾丂丂...丂(14)
(13)丆(14)傛傝丄
丂倝丂亄係倐亅俀俢亖俆們亅俋丂丂...丂(15)
(1)仈丆(15)傛傝丄
丂倝丂亅俆俙亅俀俢丂亖亅俋倐亅俋丂...丂(16)
(5)仈丆(16)傛傝丄
丂俙俢亅俆俙亅俀俢丂亖亅俋倐亅俋丂...丂(17)
(17)傪惍棟偡傞偲丂
乮俙亅俀乯乮俆亅俢乯亖俋倐亅侾丂...丂(18)
俢亝係丄倐亞侾傛傝丄俆亅俢亜侽丄俋倐亅侾亜侽偲側傞偺偱丄
俙亅俀亜侽偱側偗傟偽側傜側偄丅
堦曽丄俙亝係偱偁傞偐傜丄寢嬊丄俙亖俁倧倰俙亖係偲側傞丅
乮侾乯俙亖俁偺応崌
(18)偼丄俆亅俢亖俋倐亅侾偲側傞偑丄嵍曈偼係埲壓丄塃曈偼俉埲忋側偺偱丄夝偼懚嵼偟側偄丅
乮俀乯俙亖係偺応崌
(18)偼丄俀乮俆亅俢乯亖俋倐亅侾偲側傝丄嵍曈偼俉埲壓丄塃曈偼俉埲忋偱偁傞偐傜丄
偙偺夝偼俢亖侾丆倐亖侾偺傒偲側傞丅
偙傟傛傝丄懠偺曄悢偺抣傕埲壓偺傛偆偵妋掕偡傞丅
倎亖俀俙丂丂丂亖俉
倐丂丂丂丂丂丂亖侾丂
們亖俙亅倐丂丂亖俁
倓亖俀俢丂丂丂亖俀
倕亖俋亅倓丂丂亖俈
倖亖倕亅侾丂丂亖俇
倛亖俆們亅俉丂亖俈
倗亖係亄倖亅倛亖俁
倞亖係倐亄倗丂亖俈
倝亖侾侾亅倞丂亖係丂丂
仧嶉嬍導丂angel 偝傫偐傜偺夝摎
仜夝摎
俉亐俀亅侾亖俁 俀亄俈亅係亖俆 係亄俇亅俁亖俈 係亅俁亄俈亖俉 俉亊俀亐係亖係 俀亄俈亅俇亖俁 侾亊係亄俁亖俈 俁亊俆亄俈亖俉仜峫偊曽
丠偺儅僗傪丄嵍忋偐傜弴乮忋偺曽桪愭乯偱丄A乣J偲偟偨帪丄
1.A=2(B+C)
2.D+E=9
3.F+4=G+H
4.I+J=11
5.AD=4I
6.E=F+1
7.4B+G=J
8.5C=8+H
偺娭學幃偑弌傞丅埲壓傑偲傔偰偄偔偲丄
9.B+C亝4
忦審1傛傝
10.D(B+C)=2I
忦審1,5傛傝丅忦審5捖晠壔丄忦審1搥寢
11.F亝8
忦審6傛傝
12.D+F=8
忦審2,6傛傝丅忦審2,11捖晠壔丄忦審6搥寢
13.D亝7
忦審12傛傝丅
14.D+G+H=12
忦審3,12傛傝丅忦審3捖晠壔丄忦審12搥寢
15.I亞2
忦審4傛傝
16.4B+G+I=11
忦審4,7傛傝丅忦審7捖晠壔丄忦審4搥寢
17.(C,H)=(2,2),(3,7)
忦審8傛傝丅忦審8捖晠壔
18.(B,C,H)=(1,2,2),(1,3,7),(2,2,2)
忦審9,17傛傝丅忦審9,17捖晠壔
19.(B,C,D,G,H,I)=(1,2,2,4,2,3),(1,2,4,1,2,6),(1,3,1,5,7,2),(1,3,2,3,7,4),(1,3,3,1,7,6),(2,2,1,1,2,2)
忦審10,13,15,16,18傛傝丅忦審10,13,15,16,18捖晠壔
20.(B,C,D,G,H,I)=(1,3,2,3,7,4)
忦審14,19傛傝丅忦審14,19捖晠壔
嵟廔揑偵丄巆偭偨忦審20偲丄搥寢偟偰偄偨忦審1,4,6,12偐傜
(A,B,C,D,E,F,G,H,I,J)=(8,1,3,2,7,6,3,7,4,7)
仧垽抦導丂Y.M.Ojisan丂偝傫偐傜偺夝摎
亂夝摎亃
俉亐俀亅侾亖俁 俀亄俈亅係亖俆 係亄俇亅俁亖俈 係亅俁亄俈亖俉 俉亊俀亐係亖係 俀亄俈亅俇亖俁 侾亊係亄俁亖俈 俁亊俆亄俈亖俉亂峫偊曽亃
塃偺廲傪峫偊傞偲
乮侾乯俁亊俆亅俈亖俉丂偐丂
乮俀乯俀亊俆亅俀亖俉丂偺傒偱偁傞丅
偝傜偵乮侾乯偺応崌丂忋偺墶楍偼丂俉亐俀亅侾亖俁丂偵寛傑傝
乮俀乯偺応崌偼
乮俀亅侾乯俉亐俀亅俀亖俀丂
乮俀亅俀乯俇亐俀亅侾亖俀丂偺俀捠傝偱偁傞丅
埲忋偺俁捠傝偵懳偟丄堦売強傪枹抦悢偲偟偰曽掱幃偑摼傜傟傞丅
俁楍俁峴栚傪倶偲偡傞偲丂
乮侾乯偼倶亖俁丂
乮俀亅侾乯偼丂倶亖侾俈丂
乮俀亅俀乯偼丂倶亖侾俁偱偁傞丅
埲忋偐傜乮侾乯偺傒妋擣偡傟偽傛偄丅
仧搶嫗搒丂崟恖hide丂偝傫偐傜偺夝摎
梌偊傜傟偨栤戣傪
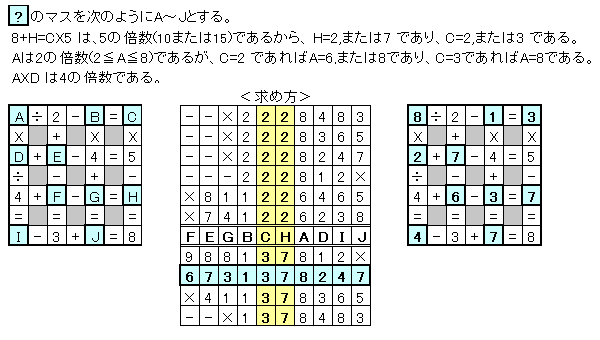
亀 丂俙亐俀亅俛亖俠 丂亊丂亄丂亊丂亊 丂俢亄俤亅係亖俆 丂亐丂亅丂亄丂亅 丂係亄俥亅俧亖俫 丂亖丂亖丂亖丂亖 丂俬亅俁亄俰亖俉 傪枮偨偡傛偆偵丄俙乣俰偵侾乣俋偺悢帤傪擖傟傛丅亁偲偟傑偡丅
傑偢丄俧,俫,俰亖侾乣俋傛傝丄俁楍栚偲係楍栚偺幃偐傜丄
俛亖侾or俀,俠亖俀or俁丂丒丒丒(1)
傪摼傑偡丅
俛丄俠偑寛傑傞偲丄侾峴栚偲係楍栚偺幃偐傜俙偲俫傕寛傑傞偺偱丄俙丄俛丄俠丄俫偺慻崌偣偼丄
乮俙,俛,俠,俫乯亖乮俉,侾,俁,俈乯,乮俉,俀,俀,俀乯,乮俇,侾,俀,俀乯
偺俁捠傝偱偡丅
偙傟傜係偮偺悢帤偑寛傑傞偲丄偁偲偼巆偭偨暥帤偺偳傟偐侾偮偺傒傪曄悢偲偟偰峫偊傞偙偲偑偱偒傑偡丅
仸亀偡側傢偪丄俢偑寛傑傟偽俀峴栚偲侾楍栚偐傜俤偲俬偑寛傑傝丄俤偑寛傑傟偽俀楍栚偐傜俥偑寛傑傝丄
俥偑寛傑傟偽俁峴栚偐傜俧偑寛傑傝丄俧偑寛傑傟偽俁楍栚偐傜俰偑寛傑傞偐傜偱偡丅
俬丄俰偑寛傑偭偨屻偵係峴栚偺幃偑惉傝棫偭偰偄傟偽丄偦傟偑摎偊偲側傞傢偗偱偡丅
偮傑傝丄俬亄俰亖侾侾偱偁傟偽傛偄偺偱偡丅亁
俢偼丄俬偑侾乣俋偱偁傞偙偲偲俙偑俇or俉偱偁傞偙偲傪峫偊傞偲偐側傝峣傜傟傞偺偱丄摎偊偼娙扨偵寛傑傞尒捠偟偑棫偪傑偡丅
傑偨丄俛亖俀偺偲偒偼俧亖侾偺傒側偺偱丄偙傟傕巊偊偦偆偱偡丅
偦傟偱偼丄幚嵺偵応崌暘偗傪偟偰峫偊偰傒傑偡丅
乮鶣乯乮俙,俛,俠,俫乯亖乮俉,侾,俁,俈乯偺偲偒
俬偑侾乣俋偱偁傞偙偲傪峫椂偡傞偲丄侾楍栚偺幃偐傜丄
俢亖侾乣係偲側傝傑偡丅
偙偺偲偒丄仸偵偟偨偑偭偰峫偊傞偲丄俢丄俤丄俥丄俧丄俬丄俰偺慻崌偣偼丄
乮俢,俤,俥,俧,俬,俰乯亖乮侾,俉,俈,係,俀,俉乯,乮俀,俈,俇,俁,係,俈乯 丂丂丂丂丂丂丂丂 乮俁,俇,俆,俀,俇,俇乯,乮係,俆,係,侾,俉,俆乯偺係捠傝偱偡丅
偙偺拞偱俬亄俰亖侾侾傪枮偨偡偺偼乮俀,俈,俇,俁,係,俈乯偺傒偱偡丅
乮鶤乯乮俙,俛,俠,俫乯亖乮俉,俀,俀,俀乯偺偲偒
俰偑侾乣俋偱偁傞偙偲傪峫椂偡傞偲丄俁楍栚偺幃偐傜丄
俧亖侾偲側傝傑偡丅
偙偺偲偒丄仸偵偟偨偑偭偰峫偊傞偲丄俢丄俤丄俥丄俧丄俬丄俰偺慻崌偣偼丄
乮俢,俤,俥,俧,俬,俰乯亖乮俋,侽,亅侾,侾,侾俉,俋乯
偺侾捠傝偱偡丅
偙傟傜偼亀壜擻側悢帤偼侾乣俋亁偺忦審傪枮偨偟偰偄側偄偺偱摎偊偵偼側傝傑偣傫丅
乮鶥乯乮俙,俛,俠,俫乯亖乮俇,侾,俀,俀乯偺偲偒
俬偑侾乣俋偱偁傞偙偲傪峫椂偡傞偲丄侾楍栚偺幃偐傜丄
俢亖俀or係or俇偲側傝傑偡丅
偙偺偲偒丄仸偵偟偨偑偭偰峫偊傞偲丄俢丄俤丄俥丄俧丄俬丄俰偺慻崌偣偼丄
乮俢,俤,俥,俧,俬,俰乯亖乮俀,俈,俇,俉,俁,侾俀乯,乮係,俆,係,俇,俇,侾侽乯乮俇,俁,俀,係,俋,俉乯
偺俁捠傝偱偡丅
偙偺拞偱俬亄俰亖侾侾傪枮偨偡傕偺偼偁傝傑偣傫丅丂丂丂
埲忋乮鶣乯乣乮鶥乯傪傑偲傔傞偲丄忦審傪枮偨偡俙乣俰偺慻崌偣偼丄
乮俙,俛,俠,俢,俤,俥,俧,俫,俬,俰乯亖乮俉,侾,俁,俀,俈,俇,俁,俈,係,俈乯
偲側傝傑偡丅
仧愮梩導丂嵷壴巕丂偝傫偐傜偺夝摎
俉亐俀亅侾亖俁 俀亄俈亅係亖俆 係亄俇亅俁亖俈 係亅俁亄俈亖俉 俉亊俀亐係亖係 俀亄俈亅俇亖俁 侾亊係亄俁亖俈 俁亊俆亄俈亖俉
丂仧 栤戣傊傕偳傞
丂仧 崱廡偺栤戣傊