◆北海道 和貴 さんからの解答
【問題1−1】
1→移動先,2,3→移動先,4→移動先,4,2→最 初,3,1→最 初, 3→移動先,1,4→移動先,2→移動先,2,1→最 初,4,3→最 初,【問題1−2】
1→移動先,2,3→移動先,4→移動先,4,2→最 初,3,1→最 初, 3→移動先,1,4→移動先,1→最 初,4→最 初,3→最 初, 3,4→移動先,1,2→移動先,【問題2−1】
1→移動先,2,3→移動先,4,5→移動先,6→移動先,6,4→最 初, 5,2→最 初,3,1→最 初,3→移動先,1,5→移動先,2,6→移動先, 4→移動先,4,2→最 初,6,1→最 初,5,3→最 初,5→移動先, 3,6→移動先,1,4→移動先,2→移動先,2,1→最 初,4,3→最 初, 6,5→最 初,
【問題2−2】
1→移動先,2,3→移動先,4,5→移動先,6→移動先,6,4→最 初, 5,2→最 初,3,1→最 初,3→移動先,1,5→移動先,2,6→移動先, 4→移動先,4,2→最 初,6,1→最 初,5,3→最 初,5→移動先, 3,6→移動先,1,4→移動先,1→最 初,4→最 初,3→最 初, 6→最 初,5→最 初,5,6→移動先,3,4→移動先,1,2→移動先,【おまけ1】
| n(n+1) 2 |
| これを、 | n 2 | 回繰り返す。 |
| 奇数番目の個数は | n 2 | +1。 |
| 偶数番目の個数は | n 2 | 。 |
| ( | n 2 |
+ | n 2 | +1)* | n 2 |
= | n(n+1) 2 | …(答) |
【おまけ2】
| n(n+3) 2 | −2 |
すべてが移動先に移動したときの2の位置は、
(n - 2* 移動した回数) であらわすことができる。
よって移動させる回数は
n−2 * x=2
| x= | n 2 | −1 より | n 2 | −1 回である。 |
| n 2 | +1+ | n 2 | なので、ここまでのすべての移動の回数は |
次に、2だけが残るように奇数番目を上から順に移動先へ移動させる。
| この試行は | n 2 | 回 …(2) である。 |
最初の場所の偶数番号をクリックして、移動先へ移動させる。
| この試行は | n 2 | 回…(4) である。 |
| n(n+3) 2 | −2…(答) |
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
【問題1−1】 10手
1,2→移動先,3,4→移動先,3→最 初,4,1→最 初,2→最 初,
2,4→移動先,1,3→移動先,1→最 初,3,2→最 初,4→最 初,
【問題1−2】 12手
1,2→移動先,3,4→移動先,3→最 初,4,1→最 初,2→最 初,
2,4→移動先,1,3→移動先,1→最 初,3,2→最 初,3→移動先,
2→移動先,1→移動先,
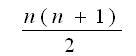
【おまけ2】 予想です
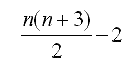
【証明】
下図(n=8の場合)のようにカードのある部分だけ上部を付き合わせると、8個のセルにカードがならび、
n+1個の位置の何れかの位置に境界が一つあるという図になる。
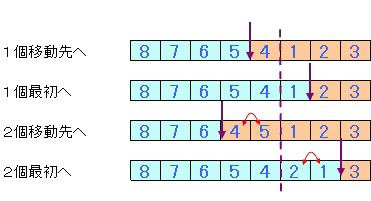
この場合、1個だけ移動するのは、境界が1個ずれるだけと同じである。
また、2個の移動は、境界が2個ずれることと、通過した2セルのカード交換が行われることと同じである。
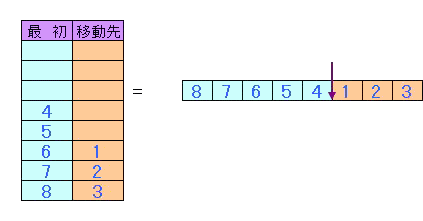
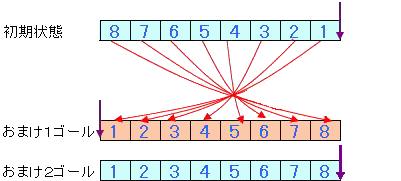
以上の表示方法で初期状態とゴール状態を表すと下図である。
いずれのゴールもカード配置にのみ注目すると逆順である。境界位置が異なっているだけである。
一方、上図に示すように1個移動ではカードの並びは変化せず、2個の場合は互換一回に対応している。
【十分条件】
【おまけ1】 下図のように左に2個2個。。。右に1個2個2個。。1個移動を 左右にn回スイープすればカード順は逆転し、かつ矢印は左端に来る。
このときの手順数は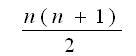 である。
である。
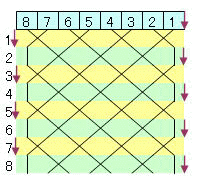
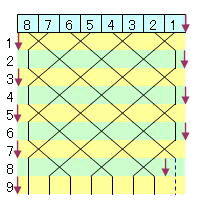
【おまけ2】 下図のようにおまけ1の最後の1手前まで実行し、そのまま1個1個1個で左に進む。
このときの手順数は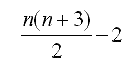 である。(青破線はそのままを表す)
である。(青破線はそのままを表す)
これは単順に、おまけ1の手順の最後を除く手順の後、1個移動のみで右へ戻る方法よりは2回少ない。
【必要条件】
N枚のカードを逆順に並び替えるには 互換は全部で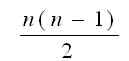 回必要である。
回必要である。
これを「必要互換数」とよぶ。
即ち、どんなに少なくても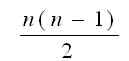 回の手数は必須である。
回の手数は必須である。
ただし、2個移動ばかりでは矢印の位置が2ずつ左右するだけなので、n=8の場合なら4回より後は戻るしかなく、かつ単純に戻るとそれは前回と同じ互換なので無駄である。
従って、状況を変えるには ここに「1個移動」を挟む必要がある。
さらに次の折り返しを考えると最後にも「1個移動」を挟む必要がある。
「よって一般には往復でn−1回連続が最高である。
これを「往復最高連続互換回数」とよぶ。
必要互換数/往復最高連続互換回数=nの半分であるので 少なくともn回の「1個移動」が余分に必要である。
nは奇数であるので、区分境界(↓)はほぼ左の端に行っている。
完全に左端にゴールするには、後1回「1個移動」が必要である。
よって、【おまけ1、2】の手数は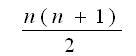 回より小さくない。
回より小さくない。
【おまけ2】の場合は、PCで虱潰しに探索したところ n=4,6,8,10の場合は十分条件で示した手数が最小であることが確認された。
多分、それ以上のときも十分条件で示した手数が最小と思われるが証明できなかった。
上記探索プログラムのソース(VC++)を添付する。 ![]()
出発と到着が反転対称の関係にあることを利用し、出発と到着両側から横型探索している。
また、順列の背番号付けで逆順列 を隣接する背番号にし、探索計算を効率化している。
◆ 問題へもどる
◆ 今週の問題へ