亂栤戣侾亃
仧杒奀摴丂僄僌僛僋僞乕 偝傫偐傜偺夝摎
20-5+2=17
仧孎杮導丂mit 偝傫丄嫗搒晎丂essential 偝傫偐傜偺夝摎
25-0!+0!
偁傑傝鉟楉偱偼偁傝傑偣傫偹丅
仧嶰廳導丂偲偔偟傫 偝傫偐傜偺夝摎
25-0!+0! 偑鉟楉側宍偩偲巚偄傑偡丅
仧媨忛導丂嶳偪傖傫 偝傫丄垽抦導丂Y.M.Ojisan丂偝傫偐傜偺夝摎
乵俀侽亄侽亅併俆乶亖侾俈
偙偙偱丄乵丂乶丗僈僂僗婰崋
乮乵丂乶偺拞偺悢傪挻偊側偄嵟戝偺惍悢乯
仧搶嫗搒丂晽壴 偝傫偐傜偺夝摎
| 5 儼 k=2 | 乮k+cos0乯亅cos0 |
儼傪巊傢側偄乮偰偄偆偐k傪巊傢側偄丠乯傕偺偱峫偊傑偟偨丅
(5-cos0)2+cos0=42+1=17
乽鉟楉乿偐偳偆偐偼傢偐傝傑偣傫偑丆僔儞僾儖偝偱偼偐側傝僀僀慄偄偭偰傞偺偱偼側偄偐偲丒丒丒丅
25-cos0+cos0=24+1=17偱傕偄偄偱偡偹丅
仧搶嫗搒丂僕儏儞僞 偝傫偐傜偺夝摎
17
=16+1
=24+1
=25-1+1
=25-cos0+cos0
傑偨偼丂佂倰伕俼丂乮擟堄偺幚悢倰乯傪傕偪偄偰
25-r^0+r0
仧奀奜丂僽儕僞 偝傫丄暉壀導偺崅峑惗丂儖乕僩係 偝傫丄晉嶳導偺崅峑惗丂T.I 偝傫偐傜偺夝摎
25-8=17丂乮8偼0偲0偺崌惉乯
仧嶉嬍導偺拞妛峑俁擭惗丂偨偗傞 偝傫偐傜偺夝摎
俆2亅俉亖侾俈丂(侽傪俀偮偔偭偮偗偰俉偵偡傞)
仧嫗搒晎偺拞妛峑俁擭惗丂pirochies 偝傫偐傜偺夝摎
俀亄俆亄俀亊俆亖侾俈
俀侽亅俆亄俀亖侾俈
俀5亅俀亊俀亊俀亖侾俈
嚁俆亄俀亖侾俈
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
2+0+0+嚁5=17
仧搶嫗搒丂愄偲偭偨媙暱 偝傫偐傜偺夝摎
20+0!-冇(5)
仧杒奀摴丂偝傓傃偲 偝傫偐傜偺夝摎
20-50=17
(俉恑朄側傜惉棫偟傑偡)
仧暉壀導丂悢妛岲偒巕 偝傫偐傜偺夝摎
乵併(俀侽侽亄俆両)乶
仧垽抦導丂柪巕偺梇擫 偝傫偐傜偺夝摎
乵俀侽亅併乮併俆侽乯乶亖[20-2.66]=17
亂栤戣俀亃
仧搶嫗搒丂偠乕 偝傫偐傜偺夝摎
亂栤戣俀亅侾亃
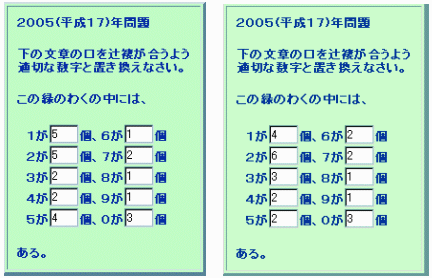
悢帤偑妋掕偡傞偲偙傠偐傜偒傔偰偄偔丅
丂悢帤丂1234567890 丂嵟掅丂2211212113(1)0偼憹偊傞偙偲偼側偄偺偱0偼3屄
丂悢帤丂123456789 丂嵟掅丂222121211(2)9傪2屄偲壖掕
丂(2)-1憹偊傞9偺応強傪2偲偡傞偲丄
丂悢帤丂123456789 丂屄悢丂292222229偲側傝丄3偼2屄偵側傜側偄偺偱柕弬
摨條偵3,4,5,6,7,8傕9偲側傜側偄
傑偨丄摨條偵9偼3屄埲忋偵側傜側偄偺偱9偼1屄
丂9仺1
丂悢帤丂12345678 丂嵟掅丂32212121(3)摨條偵8傪2屄偲壖掕
丂(3)-1憹偊傞8偺応強傪2偲偡傞偲丄
丂悢帤丂12345678 丂屄悢丂38222222偲側傝丄4偼2屄偵側傜側偄偺偱柕弬
傑偨丄摨條偵8偼3屄埲忋偵側傜側偄偺偱8偼1屄
丂8仺1
丂悢帤丂1234567 丂嵟掅丂4221212(4)摨條偵7傪3屄偲壖掕
丂(4)-1憹偊傞7偺応強傪2偲偡傞偲丄2偵側傞壜擻惈偺偁傞悢帤偼慡晹偱6屄側偺偱柕弬
丂(4)-2憹偊傞7偺応強傪3偲偡傞偲丄
丂悢帤丂1234567 丂屄悢丂4373333偲側傝丄4偼3屄偵側傜側偄偺偱柕弬
摨條偵5,6傕7偲側傜側偄
傑偨丄摨條偵7偼4屄埲忋偵側傜側偄偺偱7偼2屄
丂7仺2
丂悢帤丂123456 丂嵟掅丂432121(5)師偵1傪傒傞偲丄1偼妋掕4屄僾儔僗壜擻惈2屄偱丄嵟戝6屄偲側傞丅
丂(5)-1丂1傪6偲壖掕偡傞偲丄6偑2偵側傝丄1偼6偲側傜側偄偨傔柕弬
丂(5)-2丂1傪5偲壖掕偡傞偲丄4偐6偑1偲側傞丅
丂(5)-2-1丂4傪1偲壖掕偡傞
6傪2屄偲壖掕偡傞偲2,3,5偼6屄偵側傜側偄偺偱柕弬
摨條偵6偼3屄埲忋偲側傜側偄偺偱4偼1偲側傜側偄丅
丂(5)-2-2丂6傪1偲壖掕偡傞
丂(5)-2-2-1丂4傪2屄偲壖掕偡傞
丂(5)-2-2-1-1丂偦偺4偺応強傪2偲壖掕偡傞偲丄
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂54*2*1丂巆2偼屄悢偑妋掕偡傞丅
丂(5)-2-2-1-2丂偦偺4偺応強傪3偲壖掕偡傞偲丄
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂5342312偲5偼3傪側傞偑2偼3屄偲側傜側偄偺偱柕弬
丂(5)-2-2-1-3丂偦偺4偺応強傪5偲壖掕偡傞偲丄
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂5**241丂丂5偑4屄偵側傞偨傔偵偼2偐3偑5偩偑丄3偼5偵側傜側偄偺偱2偑5偲側傞丅
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂552241丂仺忦審傪枮偨偟惓夝 5522412113丂(5)-2-2-2丂4傪3屄偲壖掕偡傞
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂5**3*1偲2,3,5偺応強偵2偮4偑擖傞偑忦審傪枮偨偡慻傒崌傢偣偼側偄偺偱4偼3屄偲偼側傜側偄丅
丂(5)-2-2-3丂4傪4屄偲壖掕偡傞
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂5**4*1偲2,3,5偺応強偵2偮4偑擖傞偑忦審傪枮偨偡慻傒崌傢偣偼側偄偺偱4偼4屄偲偼側傜側偄丅
丂(5)-2-2-3丂4偼枹妋掕偑3偮丄偡偱偵偁傞4偑1屄傛傝丄5屄埲忋偲偼側傜側偄丅
丂(5)-3丂1傪4偲壖掕偡傞偲丄6偼2埲忋偲側傞偑3埲忋偲偼側傜側偄
乮枹妋掕偑5屄偟偐側偄偨傔椺偊偽2,3傪摨帪偵6屄偵偡傞偙偲偼偱偒側偄乯
傛偭偰
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂4****2 巆4崌寁13丂(5)-3-1丂3埲忋傪6屄偲偡傞偲丄枹妋掕4屄傛傝丄忦審傪枮偨偡慻傒崌傢偣偼側偄
丂(5)-3-2丂6偺応強傪2偲壖掕偡傞丅
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂46***2 巆3崌寁7偲3,4,5偺偆偪2偮偑2偲側傞丅
俁捠傝偺慻傒崌傢偣偺拞偱忦審傪枮偨偡偺偼
丂悢帤丂123456 丂嵟掅丂432121 丂屄悢丂463222丂仺忦審傪枮偨偟惓夝 4632222113埲忋偱慡偰偺忦審傪挷傋偨偺偱丄夝偼俀捠傝偱丄
5522412113 4632222113
亂栤戣俀亅俀亃
俀捠傝
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
亂栤戣俀亅侾亃
尰嵼偺 1偺屄悢偼4屄偱偡丅 2偺屄悢偼6屄偱偡丅 3偺屄悢偼3屄偱偡丅 4偺屄悢偼2屄偱偡丅 5偺屄悢偼2屄偱偡丅 6偺屄悢偼2屄偱偡丅 7偺屄悢偼2屄偱偡丅 8偺屄悢偼1屄偱偡丅 9偺屄悢偼1屄偱偡丅 0偺屄悢偼3屄偱偡丅 尰嵼偺 1偺屄悢偼5屄偱偡丅 2偺屄悢偼5屄偱偡丅 3偺屄悢偼2屄偱偡丅 4偺屄悢偼2屄偱偡丅 5偺屄悢偼4屄偱偡丅 6偺屄悢偼1屄偱偡丅 7偺屄悢偼2屄偱偡丅 8偺屄悢偼1屄偱偡丅 9偺屄悢偼1屄偱偡丅 0偺屄悢偼3屄偱偡丅亂栤戣俀亅俀亃
俀捠傝丅
亂偍傑偗亃
帺屓尵媦宆偺柦戣偲偄偆偺偱偟傚偆偐丠
椺偊偽壓婰偺傛偆側栤戣丅
乽侾偼仩屄偁傞丅
丂俀偼仩屄偁傞丅
丂侽偼仩屄偁傞丅乿
侽偼侾屄偁傞丅
偟偨偑偭偰丄侾偼俀屄偁傞丅
偲偙傠偑丄俀偼仩屄偵摉偰偼傑傞悢偑寛傑傜側偄丅
傛偭偰弌棃側偄栤戣偑偁傞丅
仧嶰廳導丂偲偔偟傫 偝傫偐傜偺夝摎
1偐傜弴偵4,6,3,2,2,2,2,1,1,3丅
帋峴嶖岆偱偲傝偁偊偢1夝媮傔傑偟偨丅
亂偍傑偗亃
2寘偺悢傪嫋偡偲偟偰傕榞偺拞偵
7899999999偲彂偐傟偰偄偨応崌側偳晄壜擻側帠偑傎傏帺柧側慻傒崌傢偣偑懚嵼偟傑偡丅
乮偙偺応崌9偺悢偵10偲彂偔偟偐側偄偑懠偵9偲彂偔梋抧偑巆偝傟偰偄側偄乯
梋択丗榞偺拞偵壗傕彂偐傟偰偄側偄応崌偼2寘傪嫋偡偲
11,2,1,1,1,1,1,1,1,1偲偄偆鉟楉側夝偑偁傝傑偡丅
仧奀奜丂僽儕僞 偝傫偐傜偺夝摎
亂栤戣俀亅侾亃媦傃亂栤戣俀亅俀亃
奺嬻棑偺拞偺悢帤傪偦傟偧傟A1,A2,乧,A8,A9,A0乮揧帤偼奺嬻棑偺嵍墶偺悢帤偵懳墳乯偲偍偔丅
傑偨丄A1,A2,乧,A8,A9,A0偵偁傞悢帤偑擖偭偰偄傞応崌偵丄
椢偺榞撪偱悢帤偺i傪悢偊忋偘偨屄悢傪N(i) (i=0,1,2,乧,8,9)偲偍偔丅
埲壓丄戣堄傪枮偨偡A1,A2,乧,A8,A9,A0偑懚嵼偡傞偲壖掕偟偰媍榑傪恑傔傞丅
奺嬻棑傕娷傔丄椢偺榞撪偵偼悢帤偑26屄婰擖偝傟傞偺偱丄
A1+A2+A3+A4+A5+A6+A7+A8+A9+A0=26偑惉棫偡傞丅乧(1)
奺嬻棑偺棑奜偵偼婛偵悢帤偑婰擖偝傟偰偄傞偙偲偲丄戣堄傛傝丄
2亝A1亝9, 2亝A2亝9, 1亝A3亝9, 1亝A4亝9, 2亝A5亝9,
1亝A6亝9, 2亝A7亝9, 1亝A8亝9, 1亝A9亝9, 3亝A0亝9偑惉棫偡傞丅乧(2)
(2)傛傝椢偺榞撪偵偼悢帤偺侽偺屄悢偑憹偊傞偙偲偼側偄偺偱丄
A0=3偑妋掕偡傞丅
(2)傛傝椢偺榞撪偵偍偗傞悢帤偺侾偺屄悢偺忋尷偼俈屄丅
廬偭偰2亝A1亝7丅
A9亞2偲壖掕偡傞偲丄乮A2,乧,A8乯偺偆偪彮側偔偲傕堦偮偑俋偲側傞偑丄
偄偢傟偵摉偰偼傔偰傒偰傕戣堄傪枮偨偡A1,A2,乧,A8,A9,A0偺慻傒崌傢偣偑摼傜傟側偄偙偲偐傜丄
A9=1偑妋掕偡傞丅
埲忋偺弨旛傪宱偰丄夝傪摼傞偨傔偺BASIC僾儘僌儔儉偼師偺捠傝丅
DIM N(0 TO 9)
MAT N=ZER
LET count=0
FUNCTION num(x)
LET k=0
IF x=1 THEN LET k=2
IF x=2 THEN LET k=2
IF x=3 THEN LET k=1
IF x=4 THEN LET k=1
IF x=5 THEN LET k=2
IF x=6 THEN LET k=1
IF x=7 THEN LET k=2
IF x=8 THEN LET k=1
IF x=9 THEN LET k=1
IF x=0 THEN LET k=3
IF a1=x THEN LET k=k+1
IF a2=x THEN LET k=k+1
IF a3=x THEN LET k=k+1
IF a4=x THEN LET k=k+1
IF a5=x THEN LET k=k+1
IF a6=x THEN LET k=k+1
IF a7=x THEN LET k=k+1
IF a8=x THEN LET k=k+1
IF a9=x THEN LET k=k+1
IF a0=x THEN LET k=k+1
LET num=k
END FUNCTION
FUNCTION judge(a1,b1,a2,b2,a3,b3,a4,b4,a5,b5,a6,b6,a7,b7,a8,b8,a9,b9,a0,b0)
LET k=0
IF (a1=b1) AND (a2=b2) AND (a3=b3) AND (a4=b4) AND (a5=b5) AND (a6=b6) AND (a7=b7) AND (a8=b8) AND (a9=b9) AND (a0=b0) THEN LET k=1
LET judge=k
END FUNCTION
LET a9=1
LET a0=3
FOR a8=1 TO 9
FOR a7=2 TO 9
FOR a6=1 TO 9
FOR a5=2 TO 9
FOR a4=1 TO 9
FOR a3=1 TO 9
FOR a2=2 TO 9
FOR a1=2 TO 7
IF a1+a2+a3+a4+a5+a6+a7+a8+a9+a0=26 THEN
FOR i=0 TO 9
LET N(i)=num(i)
NEXT I
IF judge(a1,N(1),a2,N(2),a3,N(3),a4,N(4),a5,N(5),a6,N(6),a7,N(7),a8,N(8),a9,N(9),a0,N(0))=1 THEN
PRINT a1;a2;a3;a4;a5;a6;a7;a8;a9;a0
END IF
END IF
NEXT A1
NEXT A2
NEXT A3
NEXT A4
NEXT A5
NEXT A6
NEXT A7
NEXT A8
END偙偺寢壥丄夝偼俀捠傝丅
乮A1,A2,乧,A8,A9,A0乯亖乮5, 5, 2, 2, 4, 1, 2, 1, 1, 3乯傑偨偼
乮A1,A2,乧,A8,A9,A0乯亖乮4, 6, 3, 2, 2, 2, 2, 1, 1, 3乯
亂偍傑偗亃
椺偊偽丄乽偙偺僇僊僇僢僐偺拞偵侾偑乮丂乯屄偁傞丅乿傗丄
乽戞俁俁栤丂偙偺僇僊僇僢僐偺拞偵俁偑乮丂乯屄偁傞丅乿偲偄偆栤戣偵偼夝偑側偄丅
偙偺応崌丄乮丂乯偺奜偵婛偵庡岅偺悢偲摨偠屄悢偩偗悢帤偑偁傞偺偑嫟捠揰偺傛偆偱偡丅
(姶憐乯
偁傑傝悢妛揑側夞摎偵側傝傑偣傫偱偟偨丅
仧帬夑導丂徏旜 偝傫偐傜偺夝摎
亂栤戣俀亅侾亃 亂栤戣俀亅俀亃
夝偼埲壓偺俀捠傝偱偡丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 乮夝侾乯 | 俆 | 俆 | 俀 | 俀 | 係 | 侾 | 俀 | 侾 | 侾 | 俁 |
| 乮夝俀乯 | 係 | 俇 | 俁 | 俀 | 俀 | 俀 | 俀 | 侾 | 侾 | 俁 |
亂偍傑偗亃
栤戣偺仩偵悢帤偑擖傜側偄帪偺 侾乣侽 偺屄悢(0)偼
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(0) ( 俀 俀 侾 侾 俀 侾 俀 侾 侾 俁 )偱偡丅埲壓丄悢帤偺擖偭偰側偄仩偼乮乯偱埻傒傑偡丅
乮侾乯 侽 偺屄悢(0)偼俁屄偱偡丅
侾乣俋偺屄悢偑屄悢(0)偺抣埲壓偵側傞偙偲偼柍偄偺偱丄侽偼俁屄偺傑傑曄傝傑偣傫丅
偙傟偵傛傝丄俁偼俀屄埲忋偵側傝傑偡丅
乮俀乯 侾 偺屄悢(0)偼俀屄偱偡丅
乮侾乯傛傝俁偼俀屄埲忋丄傑偨丄屄悢(0)傛傝彮偔側傞偙偲偼側偄偨傔丄侾偵側傟傞偺偼係丄俇丄俉丄俋偺係屄偩偗偱偡丅
偙傟偵傛傝丄俇屄埲壓偺抣偵側傝傑偡丅
埲壓丄俋丄俉丄俈丄丄丄偺弴偵偳偺傛偆側悢抣偑擖傞偺偐挷傋傑偡丅
乮俁乯 俋偺屄悢偼俀屄埲忋偵側傞偙偲偼偁傝傑偣傫丅
椺偊偽丄俀偺屄悢偑俋偵側傞偨傔偵偼丄侾丄俁乣俋偺偆偪俈偮偺仩偑俀偲側傞昁梫偑偁傝傑偡偑丄忋偺乮俀乯傛傝丄侾偼俇埲壓側偺偱側傝傑偣傫丅
偱偡偐傜丄俁乣俋傪俀屄偲偟側偗傟偽側傝傑偣傫丅
俁丄係傪俀屄偵偡傞偵偼偝傜偵仩偑昁梫偱偡偑丄偁傝傑偣傫丅
俋偼侾屄偱偡丅
乮係乯 摨條偵俉偵偮偄偰傕丄俀埲忋偵側傞偙偲偼偁傝傑偣傫丅俉偼侾屄偱偡丅
乮俆乯 摨條偵俈偵偮偄偰傕丄俁埲忋偵側傞偙偲偼偁傝傑偣傫丅俈偼俀屄偱偡丅
乮侾乯乣乮俆乯傑偱偱埲壓偺寢壥偵側傝傑偡丅
侾乣俇偺仩偵偼壗傕擖偭偰側偄帪偺屄悢(7)偱偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽
屄悢(7) 乮係 俁 俀 侾 俀 侾乯俀 侾 侾 俁
乣俇
乮俇乯 俇偺屄悢(7)偼侾屄偱偡偑丄俁屄埲忋偵側傞偙偲偼偁傝傑偣傫丅乮俇乕侾乯俇偑侾屄偺応崌傪峫偊傑偡丅屄悢(6-1)偼埲壓偺捠傝偱偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽
屄悢(6-1) 乮俆 俁 俀 侾 俀乯侾 俀 侾 侾 俁
乣俇
乮俇乕侾丄俆乕俀乯俇偑侾屄丄俆偑俀屄偺応崌傪峫偊傑偡丅屄悢偼埲壓偺捠傝偱偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽
屄悢(6-1,5-2) 乮俆 係 俀 侾乯俀 侾 俀 侾 侾 俁
乣俇
偙偺応崌丄侾偑俆傑偨偼俇屄偵側傝丄俆傑偨偼俇偺屄悢偑憹偊傞偺偱丄晄揔偱偡丅
乮俇乕侾丄俆乕俁乯俇偑侾屄丄俆偑俁屄偺応崌傪峫偊傑偡丅
屄悢偼埲壓偺捠傝偱偡丅
屄悢偑俆偲側傞仩偑悢帤偺侾乣係偵侾偮昁梫偱偡丅
塃偵乽乿偱帵偟傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽
屄悢(6-1,5-3) 乮俆 俁 俁 侾乯俁 侾 俀 侾 侾 俁 乽俆乿
乣俇
偙偺応崌丄係傪侾屄偲偡傞偲丄侾偼俇屄偲側傝丄俇偑俀屄偵側傝丄晄揔偱偡丅係傪俀屄偲偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-3,4-2) 乮俆 係 俁乯俀 俁 侾 俀 侾 侾 俁 乽係丄俆乿偙偺応崌丄俁偵俁偼擖傝傑偣傫丅
係傪俁屄偲偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-3,4-3) 乮俆 俁 係乯俁 俁 侾 俀 侾 侾 俁 乽係丄係丄俆乿偙偺応崌丄俀偼係屄偵側傜側偄偺偱丄晄揔偱偡丅
乮俇乕侾丄俆乕係乯俇偑侾屄偱丄俆偑係屄偺応崌傪峫偊傑偡丅
屄悢偼埲壓偺捠傝偱偡丅
屄悢偑俆偲側傞仩偑俀偮昁梫偱偡丅
塃偵乽乿偱帵偟傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-4) 乮俆 俁 俀 俀乯係 侾 俀 侾 侾 俁 乽俆丄俆乿侾偼俆屄偵側傝傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-4,4-2) 俆乮係 俀乯俀 係 侾 俀 侾 侾 俁 乽俆乿俁傪俀屄偵偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-4,4-2,3-2) 俆乮俆乯俀 俀 係 侾 俀 侾 侾 俁 乽俆乿偦偟偰丄俀傪俆屄偲偡傟偽堦偮栚偺夝偵側傝傑偡丅
係傪俁屄偲偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-4,4-3) 俆乮俁 俁乯俁 係 侾 俀 侾 侾 俁 乽係丄俆乿俀丄俁偺仩傪係偲俆偵偼偱偒傑偣傫偺偱丄晄揔偱偡丅
乮俇乕侾丄俆乕俆乯俇偑侾屄偱丄俆偑俆屄偺応崌傪峫偊傑偡丅
屄悢偼埲壓偺捠傝偱偡丅
屄悢偑俆偲側傞仩偑俁偮昁梫偱偡丅
塃偵乽乿偱帵偟傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-1,5-5) 乮俆 俁 俀 俀乯俆 侾 俀 侾 侾 俁 乽俆丄俆丄俆乿偙偺応崌丄俀丄俁丄係偺偆偪俀偮偺屄悢傪俆偵偟側偔偰偼側傝傑偣傫偑丄偱偒側偄偺偱丄晄揔偱偡丅
乮俇乕俀乯俇偑俀偺応崌傪峫偊傑偡丅
屄悢偼埲壓偺捠傝偱偡丅
屄悢偑俇偲側傞仩偑侾偮昁梫偱偡丅
塃偵乽乿偱帵偟傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(7) 乮係 係 俀 侾 俀乯俀 俀 侾 侾 俁 乽俇乿乮俇乕俀丄俆乕俀乯俇偑俀屄偱丄俆偑俀屄偺応崌傪峫偊傑偡丅
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-2,5-2) 乮係 俆 俀 侾乯俀 俀 俀 侾 侾 俁 乽俇乿偙偙偱丄係傪侾屄偲偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-2,5-2,4-1) 乮俆 俆 俀乯侾 俀 俀 俀 侾 侾 俁 乽俇乿偙傟偱偼俆埲忋偑俀偮憹偊傞偺偱晄揔偱偡丅
係傪俀屄偲偡傞偲丄
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-2,5-2,4-2) 乮係 俇 俀乯俀 俀 俀 俀 侾 侾 俁 乽係丄俇乿偙偙偱丄俁傪俁屄偲偡傞偲
悢 侾 俀 俁 係 俆 俇 俈 俉 俋 侽 屄悢(6-2,5-2,4-2,3-3) 乮係 俇乯俁 俀 俀 俀 俀 侾 侾 俁 乽係丄俇乿偲側傝丄侾傪係屄丄俀傪俇屄偲偡傟偽俀偮栚偺夝偵側傝傑偡丅
埲壓丄棯偟傑偡偑丄懠偺夝偼偁傝傑偣傫偱偟偨丅
姶憐偱偡丅
俀偮偺夝傪尒偰丄崌寁偑俀俇偵側傞偙偲偵婥偑偮偒傑偟偨丅
栤戣偺斖埻偵俀俇屄偺悢帤偑偁傞偺偱偡偐傜摉慠偱偡丅
偙傟傪巊偊側偄偐偲峫偊傑偟偨偑丄帄傝傑偣傫偱偟偨丅
仧搶嫗搒丂傑偭偪傖傫 偝傫偐傜偺夝摎
亂栤戣俀亅侾丄俀亅俀亃
侾侽屄偺嬻棑偵擖傞悢帤傪x1,x2,丒丒丒,x9,x0偲偍偒傑偡丅
傑偢椢偺榞撪偵偼x1乣x0傪娷傔丄寁俀俇屄偺悢帤偑偁傞偺偱
x1亄x2亄丒丒丒亄x9亄x0亖俀俇
侾乣侽偺悢帤偼慡晹侾屄埲忋偁傞偺偱x1乣x0偺側偐偵侽偼偁傝傑偣傫丅
傛偭偰x0亖俁
崱傢偐偭偰偄傞忦審傪彂偒弌偟偰傒傞偲
x0亖俁丂丂丂丂丂丂丂丂丂丂丂丂丂乮侾乯
x1亄x2亄丒丒丒亄x9亖俀俁丂丂丂乮俀乯
x1,x2,x3,x5,x7亞俀丂丂丂丂丂 丂乮俁乯
x4,x6,x8,x9亞侾丂丂丂丂丂丂丂丂乮係乯
偙偙偱x9亖俀偲壖掕偡傞偲x1乣x8偺偆偪侾屄偑俋偲側傞丅
x1亖俋偲偡傞偲x2乣x8偺偡傋偰偑侾偲側傝乮俀乯丄乮俁乯偵柕弬偡傞丅
x2亖俋偲偡傞偲x1,x3,x4,x5,x6,x7,x8偺偆偪俇屄偑俀偲側傜側偗傟偽側傜側偄丅
偙偺偲偒x1亄x2亄丒丒丒亄x9亞俀亄俋亄俀亊俇亄侾亖俀係偲側傝乮俀乯偵柕弬丅
x3埲崀傪俋偲偡傞偲榓偑偝傜偵憹偊傞偺偱x9亗俀偲傢偐傞丅
傑偨x9傪偝傜偵戝偒偔偡傞偙偲偱傕偙偺榓偼憹壛偡傞偺偱x9偼侾埲奜偁傝偊側偄偙偲偑傢偐傞丅
x0亖俁,x9亖侾丂丂丂丂丂丂丂丂 乮俆乯
x1亄x2亄丒丒丒亄x8亖俀俀丂丂丂乮俇乯
x1,x2,x3,x5,x7亞俀丂丂丂丂丂 丂乮俁乯
x4,x6,x8亞侾丂丂丂丂丂丂丂 丂丂乮俈乯
摨條偵x8亖俀偲壖掕偡傞偲x1乣x7偺偆偪侾屄偑俉偲側傞丅
x1亖俉偲偡傞偲x2乣x7偺偆偪俆屄偑侾偲側傝乮俁乯偵柕弬偡傞丅
x2亖俉偲偡傞偲x1,x3,x4,x5,x6,x7偺偆偪俆屄偑俀偲側傜側偗傟偽側傜側偄丅
偦偺偲偒乮俇乯傛傝x1,x3,x4,x5,x6,x7偺側偐偱俀偱側偄傕偺偼
俀俀亅俀乕俉乕俀亊俆亖俀偲側傝柕弬丅
x3亖俉偲偡傞偲x1,x2,x4,x5,x6,x7偼偡傋偰俁偲側傞偑
偙偺偲偒x1亄x2亄丒丒丒亄x8亖俀亄俉亄俁亊俇亖俀俉偲側傝乮俇乯偵柕弬丅
x4埲崀傪俉偲偡傞偲榓偑偝傜偵憹偊傞偺偱x8亗俀偲傢偐傞丅
x8亖俁偲壖掕偡傞偲x1乣x7偺偆偪俀屄偑俉偲側傝丄乮俁乯丄乮俈乯偐傜
x1亄x2亄丒丒丒亄x8亞俁亄俉亊俀亄俀亊俁亄侾亊俀亖俀俈偲側傝乮俇乯偵柕弬丅
x8傪偝傜偵戝偒偔偡傞偙偲偱傕偙偺榓偼憹壛偡傞偺偱x8偼侾埲奜偁傝偊側偄偙偲偑傢偐傞丅
x0亖俁,x8亖侾,x9亖侾丂丂丂丂 丂乮俉乯
x1亄x2亄丒丒丒亄x7亖俀1丂丂 丂乮俋乯
x1,x2,x3,x5,x7亞俀丂丂丂丂丂丂丂乮俁乯
x4,x6亞侾丂丂丂丂丂丂丂丂丂丂丂乮侾侽乯
x7亖俁偲壖掕偡傞偲x1乣x6偺偆偪俀屄偑俈偲側傝乮俁乯丄乮侾侽乯偐傜
x1亄x2亄丒丒丒亄x7亞俁亄俈亊俀亄俀亊俀亄侾亊俀亖俀俁偲側傝乮俋乯偵柕弬丅
x7傪偝傜偵戝偒偔偡傞偙偲偱傕偙偺榓偼憹壛偡傞偺偱x7偼俀埲奜偁傝偊側偄偙偲偑傢偐傞丅丂
x0亖俁,x7亖俀,x8亖侾,x9亖侾丂丂 丂乮侾侾乯
x1亄x2亄丒丒丒亄x6亖侾俋丂丂丂丂丂乮侾俀乯
x1,x2,x3,x5亞俀丂丂丂丂丂丂丂丂丂丂乮侾俁乯
x4,x6亞侾丂丂丂丂丂丂丂丂丂丂丂丂丂 乮侾侽乯
x6亖侾偐偮x5亖俀偲壖掕偡傞偲x1乣x4偼係埲壓偺悢偑擖傞偙偲偵側傝乮侾俀乯傪枮偨偡偨傔偵偼
x1亖x2亖x3亖x4亖係偟偐偁傝偊側偄偑丄偙傟偼侾丄俀丄俁丄係偺屄悢偲堦抳偟偰偄側偄偺偱晄揔丅
x6亖侾偐偮x5亖俁偲壖掕偡傞偲x1乣x4偺偆偪侾屄偑俆偲側傞丅
侾偼偡偱偵俆屄偁傞偺偱x1亖俆偟偐偁傝偊側偄丅
偙偺偲偒x2亄x3亄x4亖侾侽丄x2亞俁丄x3亞俁丄x4亞侾偐傜
乮x2,x3,x4乯亖
乮俁,俁,係乯乮俁,係,俁乯乮係,俁,俁乯乮俁,俆,俀乯乮係,係,俀乯
乮俆,俁,俀乯乮俁,俇,侾乯乮係,俆,侾乯乮俆,係,侾乯乮俇,俁,侾乯
偙傟傜偼偡傋偰屄悢傪惓偟偔昞偟偰偄側偄偺偱晄揔丅
x6亖侾偐偮x5亖係偲壖掕偡傞偲x1乣x4偺偆偪俀屄偑俆偲側傞丅
侾偼偡偱偵俆屄偁傞偺偱x1亖俆偱偁傝丄x2乣x4偺偆偪侾屄偑俆偲側傞丅
偙偺偲偒x2亄x3亄x4亖俋丄x2亞俁丄x3亞俀丄x4亞俀偐傜
乮x2,x3,x4乯亖
乮俁,俀,係乯乮俁,俁,俁乯乮係,俀,俁乯乮俁,係,俀乯乮係,俁,俀乯乮俆,俀,俀乯
偙傟傜偺偆偪屄悢傪惓偟偔昞偟偰偄傞偺偼乮俆,俀,俀乯偺傒丅
偙傟偼夝偲側偭偰偄傞丅
x6亖侾偐偮x5亖俆偲壖掕偡傞偲x1乣x4偺偆偪俀屄偑俆偲側傞丅
侾偼偡偱偵俆屄偁傞偺偱x1亖俆偱偁傝丄x2乣x4偺偆偪侾屄偑俆偲側傞丅
偙偺偲偒x2亄x3亄x4亖俉丄x2亞俁丄x3亞俀丄x4亞侾偐傜
乮x2,x3,x4乯亖
乮俁,俀,俁乯乮俁,俁,俀乯乮係,俀,俀乯乮俁,係,侾乯乮係,俁,侾乯乮俆,俀,侾乯
偙傟傜偺偆偪屄悢傪惓偟偔昞偟偰偄側偄偺偱晄揔丅
x6亖侾偲屌掕偡傞偲x5偑偲傝偆傞偺偼俆埲壓側偺偱丄x6亖侾偺岓曗偼傕偆柍偄丅
x6亖俀偐偮x5亖俀偲壖掕偡傞偲x1乣x4偺偆偪侾屄偑俇偲側傞丅
x1亖俇偲偡傞偲x2乣x4偺偆偪俀屄偑侾偱側偗傟偽側傜側偄偑乮侾俁乯傛傝偙傟偼晄壜擻丅
x2亖俇偲偡傞偲x1,x3,x4偺偆偪侾屄偑俀偲側傞丅
侾偼偡偱偵係屄偁傞偺偱x3,x4偺堦曽偑俀偲側傞丅
x3亖俀偲偡傞偲x1亄x4亖俈偐偮x1亞係傛傝
乮x1,x4乯亖乮係,俁乯乮俆,俀乯乮俇,侾乯偑岓曗偲側傞丅
偙傟傜偼偡傋偰屄悢傪惓偟偔昞偟偰偄側偄偺偱晄揔丅
x4亖俀偲偡傞偲x1亄x3亖俈偐偮x1亞係傛傝
乮x1,x3乯亖乮係,俁乯乮俆,俀乯乮俇,侾乯偑岓曗偲側傞丅
偙偺側偐偱屄悢傪惓偟偔昞偟偰偄傞偺偼
乮x1,x3乯亖乮係,俁乯偺傒丅偙傟偼夝偲側偭偰偄傞丅
x3亖俇偲偡傞偲x1亖x2亖x4亖俁偲偟偰傕慡懱偱俁偑俆屄偟偐側偄偺偱晄揔丅
x4亖俇偲偡傞偲x1亖x2亖x3亖係偲偟偰傕慡懱偱係偑係屄偟偐側偄偺偱晄揔丅
x6亖俀偐偮x5亖俁偲壖掕偡傞偲
x1乣x4偺偆偪侾屄偑俇丄偝傜偵暿偺侾屄偑俆偲側傞丅
偟偐偟丄x1亄x2亄x3亄x4亖侾係丄
x1亞係丄x2亞係丄x3亞俁丄x4亞侾偐傜偙傟偼晄壜擻丅丂
x6亖俀偲屌掕偡傞偲x5傪偝傜偵戝偒偔偡傞偙偲偼偱偒側偄丅
x6亖俁偐偮x5亖俀偲壖掕偡傞偲x1乣x4偺偆偪俀屄偑俇偲側傞丅
偟偐偟丄x1亄x2亄x3亄x4亖侾係丄
x1亞係丄x2亞係丄x3亞俁丄x4亞侾偐傜偙傟偼晄壜擻丅
x6亖俁偲屌掕偡傞偲x5傪偝傜偵戝偒偔偡傞偙偲偼偱偒側偄丅
x5亞俀傛傝x6傪偝傜偵戝偒偔偱偒傞壜擻惈偼柍偄丅
埲忋偐傜夝偼
乮x1,x2,x3,x4,x5x6,x7,x8,x9,x0乯亖乮5,5,2,2,4,1,2,1,1,3乯,
乮x1,x2,x3,x4,x5x6,x7,x8,x9,x0乯亖乮4,6,3,2,2,2,2,1,1,3乯偺2捠傝丅
仧垽抦導丂Y.M.Ojisan丂偝傫偐傜偺夝摎
亂栤戣俀亅侾亃

亂栤戣俀亅俀亃
忋婰俀捠傝
佹
乮侾乯丂榞偵擖傟傞悢帤偼侾乣俋偱偝傜偵徻嵶偼壓昞偱偁傞丅
廬偭偰丄侽偼俁屄偵妋掕偱偁傞丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 斖埻 | 俀乣俈 | 俀乣俋 | 侾乣俋 | 侾乣俋 | 俀乣俋 | 侾乣俋 | 俀乣俋 | 侾乣俋 | 侾乣俋 | 俁 |
乮俀乯丂悢帤偺屄悢偼慡晹偱俀俇屄偱偁傞丅
乮俁乯丂悢帤俋偺屄悢偑俀屄埲忋壜擻偐峫偊傞丅
忋昞偐傜悢帤侾偼嵟戝俈屄偱偁傝丄偙偙偼俋偱偼側偄丅
悢帤俀埲忋偑俋屄偁傞偲丄嵟掅偱傕俈売強偑俀埲忋偱側偗傟偽側傜偢悢帤侾係屄暘偱偁傞丅
偙傟偼慡晹偱悢帤偑俋亄侾係亄俁侽亄俀俋亖俀俉屄昁梫側忬懺偱偁偭偰丄俀俇屄傪挻偊傞丅
乮揧偊帤偼懳墳悢帤乯
傛偭偰悢帤俋偼侾屄偱偁傞丅
乮係乯丂悢帤俉偺屄悢偑俀屄埲忋壜擻偐峫偊傞丅
乮侾乯偺昞偲乮俁乯偐傜丄悢帤侾偼嵟戝俈屄偱偁傝丄偙偙偼俉偱偼側偄丅
悢帤俀埲忋偑俉屄偁傞偲丄嵟掅偱傕俇売強偑俀埲忋偱側偗傟偽側傜偢悢帤侾俀屄暘偱偁傞丅
偙傟偼慡晹偱悢帤偑俉亄侾俀亄俁侽亄侾俋亄俀俉亖俀俇屄偱偁偭偰丄俀俇屄挌搙偱偁傝丄攝抲偑侾捠傝偒傑傞丅
偟偐偙傟偼慡懱傪枮懌偡傞傕偺偱側偄丅
傛偭偰悢帤俉偼侾屄偱偁傞丅
乮俆乯偙偙偱斖埻傪惍棟偡傞偲丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 斖埻 | 係乣俇 | 俀乣俈 | 俀乣俈 | 侾乣俈 | 俀乣俈 | 侾乣俈 | 俀乣俈 | 侾 | 侾 | 俁 |
乮俇乯悢帤侾偑嵟戝偺俇屄偱偁傞偲偡傞偲丄悢帤俇偼俀屄埲忋偲側傝丄侾偑尭彮偡傞丅
傛偭偰丂悢帤侾偺屄悢偼係偐俆偱偁傞丅
乮俈乯悢帤俈偑俁売強埲忋偲偡傞偲丄慡晹偱悢帤偑
俆侾亄俀亊俁亄侾亄俈亄俁俈亄侾俉亄侾俋亄俁侽亖俀俈屄偱偁偭偰丄俀俇屄傪挻偊傞丅
傛偭偰悢帤俈偼俀屄偱偁傞丅
乮俉乯悢帤俇偑俁売強埲忋偲偡傞偲偁偒傜偐偵俀俇屄傪挻夁偡傞丅
傛偭偰侾屄偐俀屄偱偁傞丅
乮俋乯偙偙偱搑拞堦晹徣棯偟偰斖埻傪惍棟偡傞偲丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 斖埻 | 係乣俆 | 俁乣俇 | 俀乣俇 | 侾乣係 | 俀乣係 | 侾乣俀 | 俀 | 侾 | 侾 | 俁 |
乮侾侽乯悢帤侾偑係屄偲偡傞偲丄悢帤俇偼俀屄丅慡懱偺屄悢偐傜悢帤俆偼俀屄偵丄悢帤係偼俀屄偵妋掕丅
悢帤俁偑俇屄偵側傞偙偲偼側偔丄悢帤俀偑俇屄妋掕偟慡懱妋掕丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 斖埻 | 係 | 俇 | 俁 | 俀 | 俀 | 俀 | 俀 | 侾 | 侾 | 俁 |
乮侾侾乯悢帤侾偑俆屄偲偡傞偲丄悢帤俇偑俀屄偲偡傞偲丄慡懱偺屄悢偑挻夁偡傞偺偱侾屄偵妋掕丅
悢帤俁偑俆屄偲偡傞偲慡懱俀俈屄偱挻夁丅
係屄偲偡傞偲俀俇屄偱挌搙偩偑丄悢帤係偺悢偑崌傢側偄丅
俀丆係丆俆偑俁屄偲偡傞偲丄俁偺屄悢偵柕弬偑弌傞丅
傛偭偰悢帤俆偼係屄偱偁傝丄俀偼俆屄偵尷傜傟傞丅
埲忋傛傝壓昞傑偱峣傜傟傞丅
| 悢帤 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侽 |
| 斖埻 | 俆 | 俆 | 俀 | 俀 | 係 | 侾 | 俀 | 侾 | 侾 | 俁 |
亂偍傑偗亃
崱夞偺栤戣偵尷傟偽丄恖岥抦擻揑側庤朄偱夝偔偙偲偑壜擻偱偁傞丅
懄偪丄偡偱偵妋掕偟偰偄傞晹暘偐傜奺悢帤偺屄悢偺壓尷傪丄傑偨慡懱偱俀俇屄偺忦審偐傜忋尷傪寛傔傞庤朄偵傛傝丄扨偵摿掕悢帤枅偵斖埻傪嫹傔偰峴偒丄搑拞偱丄悢帤侾偺屄悢傪係屄偲俆屄偺応崌偵暘偗偰嵞搙峣傞偙偲偱夝偑摼傜傟偨丅

堦曽丄悢帤俁偺屄悢偱帵偟偨傛偆偵丄峴偒媗傑傞働乕僗傕偁傝丄夝偑昁偢偟傕懚嵼偡傞傢偗偱偼側偄丅
丂仧 栤戣傊傕偳傞
丂仧 崱廡偺栤戣傊