◆大阪府の高校生 Hiro さんからの解答
【問題1】
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,4)→(1,4)→(1,3)→(3,3)→(3,6)→
(4,6)→(4,7)→
【問題2】
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,8)→(4,8)→(4,4)→
(3,4)→(3,3)→(1,3)→(1,5)→(5,5)→
(5,9)→
【問題3】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 7)→( 6, 7)→
( 6, 6)→( 1, 6)→( 1, 3)→( 3, 3)→( 3, 4)→
( 4, 4)→( 4, 9)→( 6, 9)→( 6, 8)→( 3, 8)→
( 3, 5)→( 5, 5)→( 5,10)→( 6,10)→( 6,11)→
【問題4】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 8)→( 7, 8)→
( 7, 7)→( 1, 7)→( 1, 3)→( 3, 3)→( 3, 4)→
( 4, 4)→( 4,10)→( 5,10)→( 5,11)→( 7,11)→
( 7,12)→( 6,12)→( 6, 6)→( 5, 6)→( 5, 5)→
( 3, 5)→( 3, 9)→( 7, 9)→( 7,13)→
【おまけ】
一般のnに対して、
1° nが偶数の時
2° nが奇数の時
に場合わけすると、
1°では、n≧4で、
(1,1)→(1,2)→(2,2)→(2,n+1)→(n,n+1)→
(n,n)→(1,n)→(1,3)→(3,3)→(3,4)→・・・
となりここからは8手
| (k,k)→(k,k+1)→(k+1,k+1)→(k+1,n+k)→(n,n+k)→ (n,n+k-1)→(k,n+k-1)→(k,k+2)→(k+2,k+2)→。 ただしkは1≦k≦nで奇数 |
がワンセットとなり、
・・・→(n-3,n-1)→(n-1,n-1)→(n-1,2n-2)→(n,2n-2)→(n,2n-1)となる。
2°では、n≧9で、
(1,1)→(1,2)→(2,2)→(2,n+1)→(n,n+1)→
(n,n)→(1,n)→(1,3)→(3,3)→(3,4)→
(4,4)→(4,n-2)→(n-2,n-2)→(n-2,2n-3)→(n,2n-3)→
(n,2n-2)→(n-1,2n-2)→(n-1,n-1)→(4,n-1)→(4,n+3)→
(n-4,n+3)→(n-4,2n-5)→
となり、ここからは8手
| (k,n+k-1)→(n,n+k-1)→(n,n+k)→(k+1,n+k)→(k+1,k+1)→ (k,k+1)→(k,k)→(k-2,k)→(k-2,k-2)→。 だしkは1≦k≦nで奇数かつk≠1,3,n-2,2 |
がワンセットで、
・・・→(3,n+2)→(n,n+2)→(n,2n-1)となる。
経路数はnの偶奇によらず、n≧4で4(n-1)が成り立つ
◆広島県 清川 育男 さんからの解答
【問題1】
12 手
1)
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,4)→(1,4)→(1,3)→(3,3)→(3,6)→
(4,6)→(4,7)→
2)
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,6)→(3,6)→(3,3)→(1,3)→(1,4)→
(4,4)→(4,7)→
【問題2】
16 手
1)
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,5)→(1,5)→(1,3)→
(3,3)→(3,4)→(4,4)→(4,8)→(5,8)→
(5,9)→
2)
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,8)→(4,8)→(4,4)→
(3,4)→(3,3)→(1,3)→(1,5)→(5,5)→
(5,9)→
3)
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,4)→(4,4)→(4,8)→(5,8)→(5,7)→
(3,7)→(3,3)→(1,3)→(1,5)→(5,5)→
(5,9)→
【問題3】
20 手
1) ( 1, 1)→( 1, 2)→( 2, 2)→( 2, 4)→( 4, 4)→ ( 4, 7)→( 2, 7)→( 2, 5)→( 5, 5)→( 5,10)→ ( 6,10)→( 6, 9)→( 4, 9)→( 4, 8)→( 3, 8)→ ( 3, 3)→( 1, 3)→( 1, 6)→( 6, 6)→( 6,11)→ 2) ( 1, 1)→( 1, 2)→( 2, 2)→( 2, 4)→( 4, 4)→ ( 4, 9)→( 5, 9)→( 5,10)→( 6,10)→( 6, 7)→ ( 2, 7)→( 2, 5)→( 5, 5)→( 5, 8)→( 3, 8)→ ( 3, 3)→( 1, 3)→( 1, 6)→( 6, 6)→( 6,11)→他、39通り
24 手
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 4)→( 4, 4)→ ( 4, 6)→( 6, 6)→( 6, 9)→( 3, 9)→( 3, 3)→ ( 1, 3)→( 1, 7)→( 7, 7)→( 7,11)→( 5,11)→ ( 5, 5)→( 2, 5)→( 2, 8)→( 4, 8)→( 4,10)→ ( 6,10)→( 6,12)→( 7,12)→( 7,13)→他、344通りありました
【おまけ】
最少手数は、4(n-1)手。n≧4
◆東京都 藤本 さんからの解答
【問題1】
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,4)→(1,4)→(1,3)→(3,3)→(3,6)→
(4,6)→(4,7)
【問題2】
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,5)→(1,5)→(1,3)→
(3,3)→(3,4)→(4,4)→(4,8)→(5,8)→
(5,9)
【問題3】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 4)→( 4, 4)→
( 4, 9)→( 6, 9)→( 6, 6)→( 1, 6)→( 1, 3)→
( 3, 3)→( 3, 8)→( 5, 8)→( 5, 7)→( 2, 7)→
( 2, 5)→( 5, 5)→( 5,10)→( 6,10)→( 6,11)→
【問題4】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 4)→( 4, 4)→
( 4,10)→( 5,10)→( 5,11)→( 7,11)→( 7, 7)→
( 1, 7)→( 1, 3)→( 3, 3)→( 3, 9)→( 5, 9)→
( 5, 8)→( 2, 8)→( 2, 5)→( 5, 5)→( 5, 6)→
( 6, 6)→( 6,12)→( 7,12)→( 7,13)→
【おまけ】
●n:偶数のとき
最初の3手は共通
( 1, 1)→( 1, 2)→( 2, 2)→
以後 k= 1, 2,…, (n-4)/2 について
( 2k, 2k+2)→( 2k+2, 2k+2)→
をくりかえす。
次に
( n-2, 2n-3)→( n, 2n-3)→( n, n)→( 1, n)→( 1, 3)→
その後 j= 1,2,…, (n-4)/2 について
(2j+1,2j+1)→( 2j+1, n+2j)→( n-1, n+2j)→( n-1, n+2j-1)→( 2j, n+2j-1)→( 2j, 2j+3)→
をくりかえす
最後に
( n-1, n-1)→( n-1, 2n-2)→( n,2n-2)→( n,2n-1)
で終了
手数は
3 + 2×(n-4)/2 + 5 + 6×(n-4)/2 + 4 = 4(n-1)
●n:奇数のとき
最初の3手は共通
( 1, 1)→( 1, 2)→( 2, 2)→
以後 k= 1, 2,…, (n-5)/2 について
( 2k, 2k+2)→( 2k+2, 2k+2)→
をくりかえす。
次に
( n-3, 2n-4)→( n-2, 2n-4)→( n-2, 2n-3)→( n, 2n-3)→( n, n)→( 1, n)→( 1, 3)→
その後 j= 1,2,…, (n-5)/2 について
(2j+1,2j+1)→( 2j+1, n+2j)→( n-1, n+2j)→( n-1, n+2j-1)→( 2j, n+2j-1)→( 2j, 2j+3)→
をくりかえす
最後に
( n-2, n-2)→( n-2, n-1)→( n-1, n-1)→( n-1, 2n-2)→( n,2n-2)→( n,2n-1)
で終了
手数は
3 + 2×(n-5)/2 + 7 + 6×(n-5)/2 + 6 = 4(n-1)
以上から、手数は n(≧4)について 4( n - 1) 手
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 12回
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,4)→(1,4)→(1,3)→(3,3)→(3,6)→
(4,6)→(4,7)
【問題2】 16回
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,5)→(1,5)→(1,3)→
(3,3)→(3,4)→(4,4)→(4,8)→(5,8)→
(5,9)
【問題3】 20回
(1,1)→(1,2)→(2,2)→(2,4)→(4,4)→
(4,9)→(6,9)→(6,6)→(1,6)→(1,3)→
(3,3)→(3,8)→(5,8)→(5,7)→(2,7)→
(2,5)→(5,5)→(5,10)→(6,10)→(6,11)
【問題4】 24回
(1,1)→(1,2)→(2,2)→(2,4)→(4,4)→
(4,6)→(6,6)→(6,9)→(3,9)→(3,3)→
(1,3)→(1,7)→(7,7)→(7,11)→(5,11)→
(5,5)→(2,5)→(2,8)→(4,8)→(4,10)→
(6,10)→(6,12)→(7,12)→(7,13)
【おまけ】
最少手数=4n−4回 である。
ただし、nは偶数ないし5以上の奇数。
従って、問題1〜4の解答は最小手数である。
∵ 必要条件の証明 (n≧2とする。)
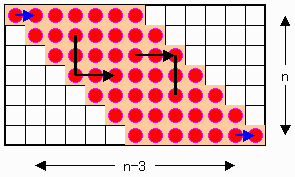
下図青矢印で示す位置は開始点ないし終了点である。
従って、黒矢印で示すように、角になっている石は通過点になる必要がある。
即ち、縦に通過する手順は少なくとも2n−3回必要である。
これら縦に通過する手順では、1回に付き少なくとも入り口出口の2個の石を拾う必要がある。
以上に開始及び終了の2個を加えると4n−4回は最低必要であることがわかる。

∵ 十分条件の証明 (n≧2とする)
下図に示すように、一般にn+2の場合を、8回でnの場合と同等にできる。
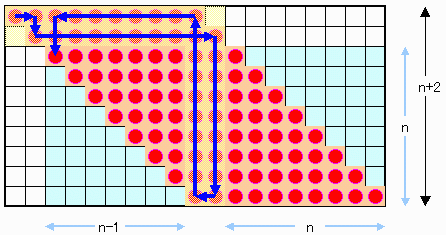
ところで、下図に示すように n=2およびn=5の場合は成立している。
よって一般iにnが偶数および5以上のとき、4nー4回の取り方が存在している。
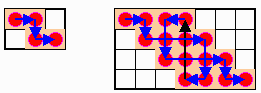
因みにn=1の時は1回 、n=3の時は不可能である。
◆東京都 ぽこぺん さんからの解答
【定義】
【定理1】

(証明)略
【定理2】
サイズ n の問題において,一つの解経路上には屈曲点が少なくとも 4n-6 個存在する。
(証明)
一つの列に上右または上左の屈曲点があれば,同じ列に下右または下左の屈曲点がなければならず,その逆も言える。
定理1により,2≦c≦n に対して (c, c) が上右屈曲点,
n≦c≦2n-2 に対して (c-n+1, c) が下左屈曲点になっているから,
第 c 列(2≦c≦2n-2)には少なくとも 1 組ずつの屈曲点が存在し,
全体として 2(2n-3) 個の屈曲点が存在する。■
注: 問題の解手順では,少なくともこれに両端点を加えた
2(2n-3)+2 = 4(n-1) 個の石を拾わなくてはならない。
【定理3】
サイズ n の問題において,もし,屈曲点をちょうど 4n-6 個含む解経路があるとすれば,
経路上で (1, n) と (n, n) は直接結ばれる。
(つまり,この 2 点を結ぶ線分上の点はすべて(上下または十字の)貫通点である)
(証明)
屈曲点が 4n-6 個なので,定理2より第 c 列(2≦c≦2n-2)にはちょうど上下 1 組ずつの屈曲点が存在する。
定理1より (1, n) と (n, n) は屈曲点なので,第 n 列にはこれ以外の屈曲点がない。■
【定理4】
ある n(n≧4) に対して屈曲点をちょうど 4n-6 個含む解が存在すれば,
n+2 に対して屈曲点をちょうど 4(n+2)-6 個含む解が存在する。
(証明)
サイズ n に対する解が存在すると仮定する。(下図)
ただし,下図では 〓 によりすでに通過している点を表す。
また,定理3による (1, n),(n, n) 間の経路上の上下または十字貫通点を ┃ で表す。
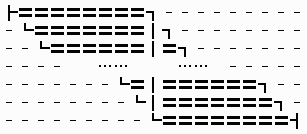
このとき,次の手順により,サイズ n の解経路を n+2 の経路に拡張することができる。
(1) 下に 2 行追加する。
(2) (n, 2n-1) の端点を下左屈曲点に変える。
(3) 第 n 列より右側にあるすべての列を右に 2 つ平行移動する。
(4) 第 n+1,n+2 列と第 n+1,n+2 行に,下図の細線のような経路を追加する。
ただし,第 n+1,n+2 列に対しては,第 2〜n 行の貫通点は第 n 列と同じ種類とする。
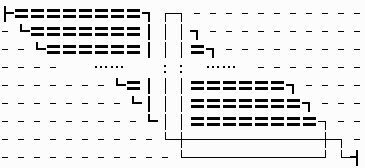
これが解経路になっていることは明らかであり,
屈曲点は 8 個増えているので,4(n+2)-6 個となる。■
【定理5】
任意の n(n≧4)に対して,屈曲点をちょうど 4n-6 個含む解経路が存在する。
(証明)
n = 4 と 5 には屈曲点をちょうど 4n-6 個含む解が存在する。(下図)
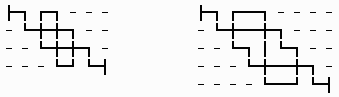
したがって,定理4により,任意の n に対して屈曲点をちょうど 4n-6 個含む解経路が存在する。■
【問題の答え】
以上の定理1〜5により,サイズ n の問題に対する最小の解手数は
4n - 6 + 2 = 4(n-1) 回となる。
解経路は,n = 4,5 に対しては,定理5の証明中の経路のみであり,この 2 例は図の中心に対して回転対称になっている。
n≧6 に対しては,回転対称のものと非対称のものとがあり,非対称の解は 2 個ずつが回転移動で重なり合う。
6≦n≦8 に対する回転対称解の一例は下図のとおりである。
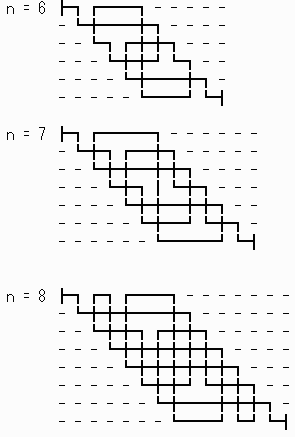
【付録】
小さいサイズに対し,最小手数の解の個数は下表のようになる。
ただし,非対称のものについては,回転移動で重なり合う解は同一視している。
| サイズ | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 回転対称 | 1 | 1 | 1 | 2 | 8 | 11 | 81 | 112 | 1057 |
| 非対称 | 0 | 0 | 1 | 9 | ? | ? | ? | ? | ? |
注: サイズの偶奇によって解の性質が異なるので,解の個数の漸近的な性質は偶奇によって
1,1, 8, 81,1057,… 1,2,11,112,…のように別々に考えるべきだが,現在のところまだ不明である。
◆東京都 明 さんからの解答
【問題1】
(1,1)→(1,2)→(2,2)→(2,5)→(4,5)→
(4,6)→(3,6)→(3,3)→(1,3)→(1,4)→
(4,4)→(4,7)
【問題2】
(1,1)→(1,2)→(2,2)→(2,6)→(3,6)→
(3,7)→(5,7)→(5,8)→(4,8)→(4,4)→
(3,4)→(3,3)→(1,3)→(1,5)→(5,5)→
(5,9)
【問題3】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 7)→( 6, 7)→
( 6, 6)→( 1, 6)→( 1, 3)→( 3, 3)→( 3, 4)→
( 4, 4)→( 4, 9)→( 6, 9)→( 6, 8)→( 3, 8)→
( 3, 5)→( 5, 5)→( 5,10)→( 6,10)→( 6,11)
【問題4】
( 1, 1)→( 1, 2)→( 2, 2)→( 2, 8)→( 4, 8)→
( 4,10)→( 5,10)→( 5,11)→( 7,11)→( 7,12)→
( 6,12)→( 6, 6)→( 4, 6)→( 4, 4)→( 3, 4)→
( 3, 5)→( 5, 5)→( 5, 9)→( 3, 9)→( 3, 3)→
( 1, 3)→( 1, 7)→( 7, 7)→( 7,13)
【おまけ】
最小手数は4(n-1)となります。
拾い尽くす考え方を以下に示します。
実際に碁石拾いを実行してみると、間もなく方向転換をする場所(以下説明のために「転向点」と呼びます)の数は、始点と終点を含む一番上と一番下以外の行では偶数となることに気が付きました。
これは碁石拾いの経路を考えると、一番上と一番下以外の行では、他の行から該当行へ経路が選択され、転向点が設定されたときは、その後行方向へ石を拾った後、必ず別の転向点から他の行へ経路を変更しなければならないからと判ります。
(一筆書きと同じ理屈です。)
また一番上と一番下の始点と終点を含む行では同様の理由から転向点は奇数とならなくてはなりません。
全く同じ理由から、列方向でも転向点の数は偶数でなくてはなりません。
また端の石は、この石を拾うために転向点とならなければなりません。
以上が碁石拾いを完成させるための、転向点の必要条件となります。
n=4のとき、端の石を転向点と決め、その後、行、列の偶奇条件で転向点を設定すると、下記のようになります。
また、必要条件を満たす転向点の配置はこの図のみです。
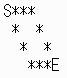
(Sが始点、Eが終点、*が転向点を表します。)
この図で碁石拾いを行うと、自動的にすべての石を拾うことができます。
ちなみに拾い方は2通りとなります。
必要条件を満たすための転向点の最小数は 2(2n-3)となります。
始点と終点の数を加えると、4n-4=4(n-1)となり、これが碁石拾いの手数の下限値となります。
さらに下限値の転向点で碁石拾いを完成させる配置が以下のように存在します。
●nが偶数の時、
端の石と、一番上と一番下の行のすべての石をを転向点とする。
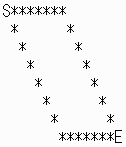
●nが奇数の時
端の石はすべて転向点。
一番上および一番下の行はそれぞれ始点、終点からn-1番目の石を除いてすべて転向点。
| n-1列目とn+1列目の転向点を | 2n+1 2 | 行目に設定する。 |

以上の図で碁石拾いを行うと、自動的にすべての石を拾うことができます。
なお終点の石を最後に拾うことに留意しておく必要があるかもしれません。
碁石拾いを完成させる転向点の配置は他にもありますが、すべてを洗いつくすのはむずかしそうです。
なお、余談ですが、n=3のときは転向点の下限値が6になり、一方、偶奇性を満たして行の転向点を配置するには最大4しかなく、下限値を満たせないことから、碁石拾いを完成させることができないことが証明できます。
(証明するまでもなく、実際やって見れば自明ですが)
◆ 問題へもどる
◆ 今週の問題へ