◆広島県 清川 育男 さんからの解答
【問題1】
15 手NO. 1
b→f→d→c→a→b→d→e→g→f→
b→d→c→e→d
すべての解はこちらです。(48通り)
◆静岡県 medaka さんからの解答
【問題1】
以下の15手。
b→f→d→c→a→b→d→e→g→f→ b→d→c→e→d探索プログラムをprologで作成して,最短手数を求めました。
scan(N):-ida([],N,[1,1,1,0,2,2,2],[2,2,2,0,1,1,1]).
ida(OP,MaxDepth,Goal,Goal):-print('*** congratulation ***'),nl,print(OP).
ida(OP,MaxDepth,A,Goal) :-length(OP,L),L<MaxDepth,
rule(S,A,B),
ida([S|OP],MaxDepth,B,Goal).
% pos-A
rule(b,[0,B,C,D,E,F,G],[B,0,C,D,E,F,G]).
rule(c,[0,B,C,D,E,F,G],[C,B,0,D,E,F,G]).
% pos-B
rule(a,[A,0,C,D,E,F,G],[0,A,C,D,E,F,G]).
rule(d,[A,0,C,D,E,F,G],[A,D,C,0,E,F,G]).
rule(f,[A,0,C,D,E,F,G],[A,F,C,D,E,0,G]).
% pos-C
rule(a,[A,B,0,D,E,F,G],[0,B,A,D,E,F,G]).
rule(d,[A,B,0,D,E,F,G],[A,B,D,0,E,F,G]).
rule(e,[A,B,0,D,E,F,G],[A,B,E,D,0,F,G]).
% pos-D
rule(b,[A,B,C,0,E,F,G],[A,0,C,B,E,F,G]).
rule(c,[A,B,C,0,E,F,G],[A,B,0,C,E,F,G]).
rule(e,[A,B,C,0,E,F,G],[A,B,C,E,0,F,G]).
rule(f,[A,B,C,0,E,F,G],[A,B,C,F,E,0,G]).
% pos-E
rule(d,[A,B,C,D,0,F,G],[A,B,C,0,D,F,G]).
rule(g,[A,B,C,D,0,F,G],[A,B,C,D,G,F,0]).
rule(c,[A,B,C,D,0,F,G],[A,B,0,D,C,F,G]).
% pos-F
rule(d,[A,B,C,D,E,0,G],[A,B,C,0,E,D,G]).
rule(g,[A,B,C,D,E,0,G],[A,B,C,D,E,G,0]).
rule(b,[A,B,C,D,E,0,G],[A,0,C,D,E,B,G]).
% pos-G
rule(e,[A,B,C,D,E,F,0],[A,B,C,D,0,F,E]).
rule(f,[A,B,C,D,E,F,0],[A,B,C,D,E,0,F]).
◆浜田 明巳 さんからの解答
蛙の位置に
| 1 | 2 | |
| 3 | 4 | 5 |
| 6 | 7 |
| A | A | |
| A | O | B |
| B | B |
というように1〜7の番号をつける.
そして次の20種類の移動を考える.
1 1->2 2 2->1 3 1->3 4 3->1 5 2->4 6 4->2 7 2->6 8 6->2 9 3->4 10 4->3 11 3->5 12 5->3 13 4->5 14 5->4 15 4->6 16 6->4 17 5->7 18 7->5 19 6->7 20 7->6対称性から,最初の移動は,移動5の2->4でいいことが分かる.
次にその移動例を示す.
AA A B BB 2->4(1回目) A AAB BB 6->2(2回目) AB AAB B 4->6(3回目) AB A B AB 3->4(4回目) AB AB AB 1->3(5回目) B AAB AB 2->1(6回目) B AAB AB 4->2(7回目) BA A B AB 5->4(8回目) BA AB AB 7->5(9回目) BA ABB A 6->7(10回目) BA ABB A 2->6(11回目) B ABB AA 4->2(12回目) BB A B AA 3->4(13回目) BB AB AA 5->3(14回目) BB BA AA 4->5(15回目) BB B A AA
Option Explicit
Const MAX As Integer = 20 '移動の回数の最大値
' A A
' A 0 B
' B B
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 8).Value = 0
Range("H2").Select
'
Dim a(MAX) As Integer
Dim m As Integer '移動の回数
a(1) = 5 '最初は2->4としてよい
m = 2
While Cells(1, 8).Value = 0 And m <= MAX
Cells(2, 8).Value = m
Call saiki(m, 2, a())
m = m + 1
Wend
End Sub
Sub saiki(ByVal m As Integer, ByVal n As Integer, ByRef a() As Integer)
Dim b(7) As Integer '蛙の種類,A:1,B:2,なし:0
Dim b1 As Integer '移動元の蛙
Dim b2 As Integer '移動先の蛙
Dim j As Integer
Dim dame As Integer
a(n) = 1
While a(n) <= 20
If a(n - 1) = a(n) Then '同じ移動の繰り返しはだめ
dame = 1
ElseIf a(n) Mod 2 = 0 And a(n) = a(n - 1) + 1 Then '元に戻る移動はだめ
dame = 1
ElseIf a(n) Mod 2 And a(n) = a(n - 1) - 1 Then
dame = 1
Else
dame = 0
End If
If dame = 0 Then
b(1) = 1
b(2) = 1
b(3) = 1
b(4) = 0
b(5) = 2
b(6) = 2
b(7) = 2
For j = 1 To n
b1 = b(Cells(a(j), 1).Value)
b2 = b(Cells(a(j), 2).Value)
If b1 = 0 Or b2 > 0 Then
dame = 1
ElseIf a(j) = 7 Or a(j) = 8 Or a(j) = 11 Or a(j) = 12 Then '1つ飛び越える場合
If b(4) = 0 Then
dame = 1
Else
Select Case a(j)
Case 7
dame = -(b(2) = b(4))
Case 8
dame = -(b(6) = b(4))
Case 11
dame = -(b(3) = b(4))
Case Else
dame = -(b(5) = b(4))
End Select
End If
End If
If dame = 0 Then
b(Cells(a(j), 1).Value) = 0
b(Cells(a(j), 2).Value) = b1
End If
Next j
If dame = 0 Then
If b(1) = 2 And b(2) = 2 And b(3) = 2 And b(5) = 1 And b(6) = 1 And b(7) = 1 Then
Cells(1, 8).Value = Cells(1, 8).Value + 1
For j = 1 To n
Cells(Cells(1, 8).Value, j + 8).Value = a(j)
Next j
ElseIf n < m Then
Call saiki(m, n + 1, a())
End If
End If
End If
a(n) = a(n) + 1
Wend
End Sub
◆東京都 ぽこぺん さんからの解答
【1】 カエルの配置の点数
初期配置で赤カエル,青カエルがいるセルをそれぞれ「赤領域」,「青領域」と呼び,どちらにも属さないセルを「中心」と呼ぶ。
また,初期配置から最終配置に至る手順を「解手順」と呼ぶことにする。
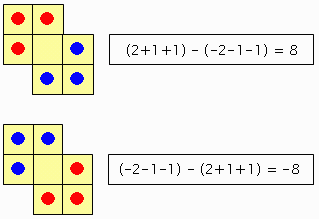
盤面の各セルに次の重みを設定する:
| +2 | +1 | |
| +1 | 0 | −1 |
| −1 | −2 |
また,赤カエルには+1点,青カエルには-1点を与え,6匹のカエルの一つの配置に対して
(各カエルの点数)×(そのカエルが位置するセルの重み)
という積の和をこの配置に対する点数として定義し,「配置得点」と呼ぶ。
これにより,初期配置と最終配置の得点は,それぞれ

のように8点と-8点となる。
明らかに,これが配置得点の最大・最小値である。
【2】 カエルの移動に伴う配置得点の変化
(A) 空セルの隣りのセルにいるカエルが空セルに移動する場合(S移動と呼ぶ)
その2つ以外のセルにいるカエルは点数の変化に寄与しない。
このとき,隣り合うセルの重みはどこでも差が1であるから,配置得点は1だけ変化する。
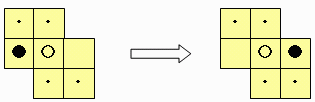
(B) カエルが異なる色のカエルを飛び越す場合(J移動と呼ぶ)
この場合も,カエルの移動前のセルと移動後のセル以外のセルにいるカエルは点数の変化に寄与しない。
この移動には,中央のセルを飛び越す場合(下図の例)しかないから,配置得点は2だけ変化する。
【3】 分布指標 DI の定義
カエルの配置の特徴を表す第2の量を次のように定義し,
「分布指標(DI; Distribution Index)」と呼ぶ。
[ 赤領域の赤カエルの個数,赤領域の青カエルの個数;中心の色;青領域の赤カエルの個数,青領域の青カエルの個数 ]これは冗長ではあるが,見やすさを考慮したものである。
[3, 0; E; 0, 3],[2, 0; R; 0, 3],[3, 0; B; 0, 2], [2, 1; E; 1, 2],[1, 1; R; 1, 2],[2, 1; R; 0, 2],[2, 1; B; 1, 1],[2, 0; B; 1, 2], [1, 2; E; 2, 1],[1, 2; R; 1, 1],[0, 2; R; 2, 1],[1, 1; B; 2, 1],[1, 2; B; 2, 0] [0, 3; E; 3, 0],[0, 3; R; 2, 0],[0, 2; B; 3, 0]ここで,各行の左端のDIを持つ配置と,その行の右に並ぶDIを持つ配置とは,相互にS移動で移ることができる。
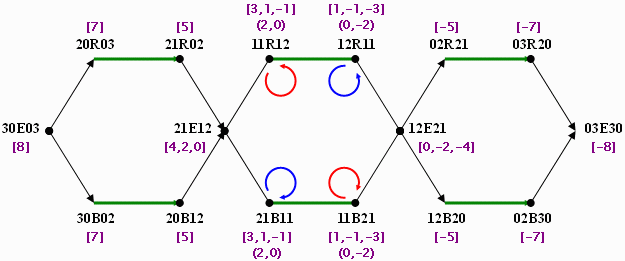
これを「解グラフ」と呼ぶ。
この図で,各節点はDIに対応している(DIはカッコや区切り記号を除いて内容だけで示し,それを節点名に代用する)。
黒線はDIに対応する配置間のS移動を表し,緑線はJ移動を表す。
また,赤・青の円弧は同じDIに対応する配置の間でS移動を2回連続して行う移動を表すが,これはそれぞれ赤領域・青領域の中で空セルがL字型に移動することに対応している。
この2回のS移動の組み合わせを特に「L移動」と呼ぶ。
カギカッコ中の数のリストは,そのDIに対応する配置得点の取り得る値を表す。
ただし,L移動中に現れる配置得点は,節点から別の節点への移動には関与しないので丸カッコで別に表した。
問題の解は,解グラフにおいて初期配置(左端)から最終配置(右端)に至る可能な(つまり実際の配置に対応する)パスにより表される。
各辺を右方向に進むと配置得点は減り(S移動では-1,J移動では-2),左方向に進むと増える(同様)。
最短の解手順を求めるため,同じ移動の正・逆を連続して行うような無意味な移動は考慮しない。
このとき,左端の30E03から21E12へ 8→7→5→4 と進むパスと,12E21から右端の03E30へ -4→-5→-7→-8 と進むパスは,どちらも右方向へ進む場合しかあり得ないので,そのことを矢印により示す。
【4】 最短の解手順が15回であることの証明
(1) 解手順にはL移動が少なくとも2回含まれる
赤と青のカエルは相手領域の最奥(重みが±2)のセルに入らなければならず,それはL移動によってのみ実現できる。
したがって,解グラフの赤の円弧,青の円弧を少なくとも1度ずつたどらなくてはならない。
(2) 最短の解手順において配置得点の変化が単調減少であることはない
配置得点の変化が単調減少である解が存在したとすれば,それは解グラフの中央の六角形の部分グラフにおいて,得点の変化が
4 → (3→2→1) ⇒ (-1→-2→-3) → -4
となる場合しかあり得ない。
ただし,カッコ内はL移動を表す。このようなDIの列は,
21E12 →(11R12→11R12→11R12)⇒(12R11→12R11→12R11)→ 12E21 21E12 →(21B11→21B11→21B11)⇒(11B21→11B21→11B21)→ 12E21となるが,それに対応する配置は

か,またはこれと対称なものしかない。
しかし,この両端の配置は中心の両側が同色であるため,S移動1回ではJ移動と結び付けることができない。
したがって,解グラフのこのような単調減少のパスに対応する実際の配置は存在しない。
(3) 最短の解手順は15回である
前項の結果より,中央の六角形の部分グラフを7手順で通過する解手順は存在しない。
ここにL移動を追加したり,辺の往復を追加したりしても,この部分を8手順で通過することはできないから,少なくとも9手順が必要である。
制約 (1) を満たし,ここを9手順で通過するパスとしては,
21E12 → (21B11)3 → 21E12 → (11R12)3 ⇒ 12R11 → 12E21 21E12 → 11R12 ⇒ (12R11)3 → 12E21 → (11B21)3 → 12E21 21E12 → 11R12 ⇒ (12R11)3 ⇒ (11R12)3 ⇒ 12R11 → 12E21という3種類(およびグラフを上下に反転したもの)があるが,実際,それぞれに対応して
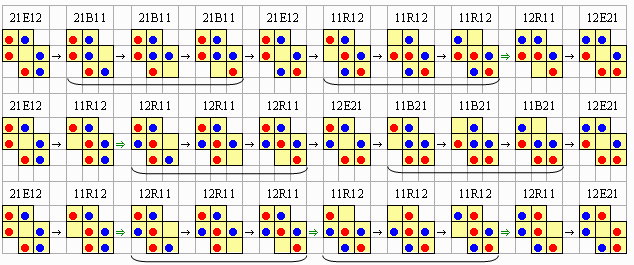
のような配置の列が存在し,両端から外側に向かうパスも明らかに実際の配置の列に対応するから,これは(部分)解手順になっている。
このことから,最短の解手順は中央の9手順に,左右のそれぞれ3手順を加えて,全体として15手順ということになる。
【5】 最短解の個数
前項のように,得点4の21E12から得点-4の12E21へ至る部分解手順に対応するパスは3種類あり,それぞれに上下反転したパスがある。
そのそれぞれに対し,実際の部分解手順は,上図に掲げた手順と,それを\方向に反転したものとがある。
さらに,そのそれぞれに対し,左側に手順を付加する方法に2通り,右側にも同様に2通りの可能な方法がある。
以上より,3×2×2×2×2 = 48(通り)の解手順が存在することがわかる。
なお,解の間の対応関係に関しては,次のことが言える。
前項の最後に示した3種類の部分解手順を順にA型,B型,C型とすると,A型,B型が1個のJ移動を含むのに対して,C型は3個のJ移動を含むので,両者は本質的に異なる。
また,A型の部分解手順に含まれる各配置を中心セルの/方向の対角線に関して反転し,配置を逆順に並べ替えるとB型の部分解手順に重なるので,この間には1対1の対応関係がある。
C型に関しては,各配置を中心セルの中心に関して180°回転し,配置を逆順に並べ替えると自分自身に重なる。
このことから,非常におおざっぱに言うと,本質的に異なる解はA・B型とC型との2種類しかないということになる。
(図形的な対称性の点では,上記の部分解手順の外側に付加する手順により,いくつかの本質的でない非対称性が現れる)
【6】 問題の拡張
問題を,n×nの正方形が1セルを共有するように拡張した場合には,本解答の方法を同様に拡張して使うことができる。
別の拡張として,1頂点を共有する3つの三角形の形状に n-1 段に並べた(下図はn=4の場合)3色のコマを,中央の空セルを通じて輪環状に入れ替える(青→緑→赤など)という問題が考えられる。
ただし,コマの動かし方は本問と同じとし,黒線でつながれたセルを「隣りのセル」と定義するものとする。
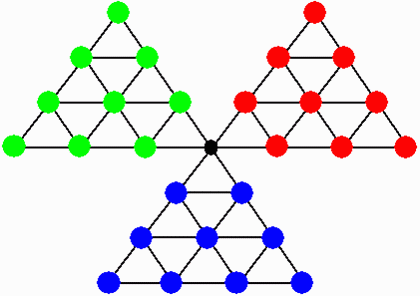
(確か,「三角ソリテア」といったような名前で,大昔にどこかで見たことがあるような...)
◆ 問題へもどる
◆ 今週の問題へ