◆広島県 清川 育男 さんからの解答
【問題1】●●□□●
□□□□□
□●□□□
□□□□□
□□□●□
□□□□□
□□□□●
□□□●□
●□□□□
●□□□●
【おまけ1】
280 通り。
【問題2】●●□□□□
□□□●□□
□□□□□□
□□□□□●
□□□□□□
□□●□□●
□□□□□●
□□□□□□
□□□□□●
□□●□□□
●●□□□□
□□□□□●
【おまけ2】
16 通り。
【おまけ3】
7*7
1 3 10 21 22 41 49
1 4 15 16 41 45 49
1 5 9 34 35 46 49
1 9 28 29 40 47 49
3 7 13 29 30 43 46
4 7 20 21 37 43 47
5 7 12 15 28 37 43
7 13 22 35 38 43 45
8通り。
8*8 解なし。
◆千葉県 菜花子 さんからの解答

◆静岡県 medaka さんからの解答
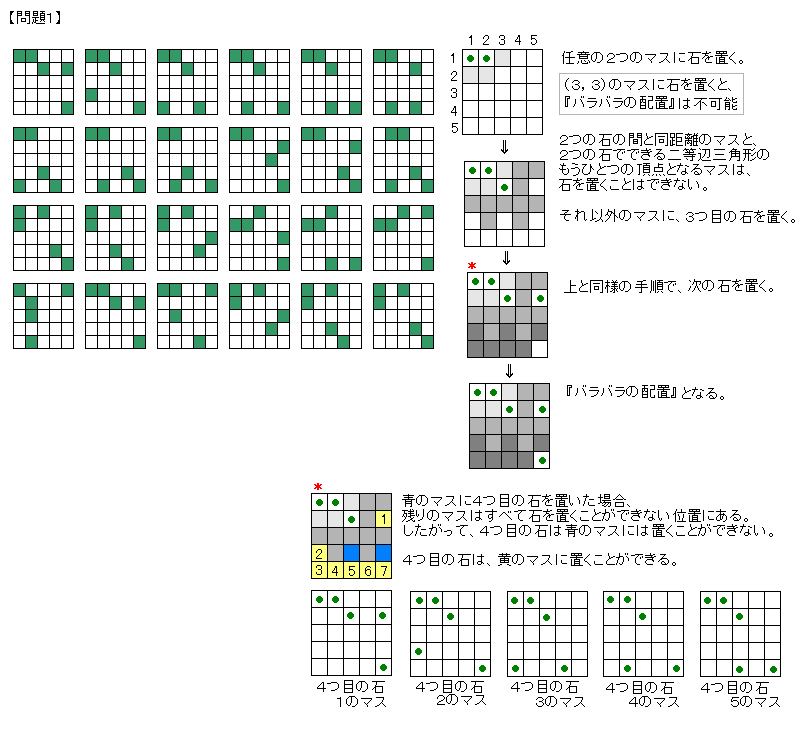
【問題1】
石の位置を●で表す。
○○○○●
○○○●○
○○○○○
○○○○●
●●○○○
考え方:なるべく距離の長い配置を先に決定し、残り石で調整した。
【問題2】
(答え) (2つしかない解のうちの1つ)
●○○○○○
○○○○●●
○○○●○○
●○○○○○
○○○○○○
●○○○○○
【おまけ1】
(答え) 5x5の解の数 35通り。
ただし、鏡像解を別解としてカウントする場合は280通り。
(解法)
プログラムによる探索で全数を求めた。
(プログラムは、最後に添付)
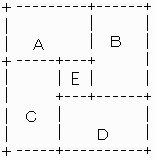
5x5の領域を2x3の4つの領域A,B,C,Dと中央に1x1のEの領域に分けて考える。
2x3の領域の中に配置された石の配置をもとめ、それを基に、5x5の領域の配置を求めた。
(2x3の領域に配置できる石の数は最大で3個である)
【おまけ2】
(答え) 6x6の解の数 以下の2通り。
ただし、鏡像解を別解としてカウントする場合は16通り。
●○○○○○
○○○○●●
○○○●○○
●○○○○○
○○○○○○
●○○○○○
○○○●○●
○○○○○○
○●○○○○
○○○○○●
●○○○○○
●○○○○○
(解法)
プログラムによる探索で全数を求めた。
(プログラムは、5x5と類似しているので割愛した)
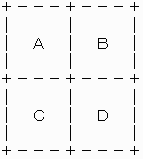
6x6の領域を3x3の4つの領域A,B,C,Dに分けて考える。
3x3の領域の中に配置された石の配置をもとめ、それを基に、6x6の領域の配置を求めた。
(3x3の領域に配置できる石の数は最大で3個である)
◆5x5の配置を求めるプログラム
##### 20004.04.18
#
# Size = 5
def exe() :
global Ans
out = open("w5log.txt","w")
M = Init(out)
Ans = []
Total = 0
for E in range(0,2) :
for A in range(3,1,-1) :
for B in range(A,-1,-1) :
for C in range(A,-1,-1) :
if C > B : continue
D = 5 - (A+B+C+E)
if D < 0 : continue
if D > A : break
Cnt = Join(M,A,B,C,D,E,out)
Total += Cnt
WriteLog(out,"\n (%d,%d,%d,%d,%d) : %4d %4d" % (A,B,C,D,E,Cnt,Total))
out.close()
###
def Init(out) :
global BitMask
BitMask = [1L]
for i in range(1,34) : BitMask += [BitMask[i-1] << 1]
M = [[],[],[],[]]
for k in range(0,64) :
b = Bits(k)
if b > 3 : continue
w = k
p = 0
pos = []
while w != 0 :
if w & 0x01 : pos += [[p%3,p/3]]
w = w >> 1
p += 1
[m,pos2] = NormCheck(0,[],pos)
if m == -1 : continue
M[b] += [[k,pos]]
# for i in range(0,4) :
# WriteLog(out,"\n ==== %d ====" % (i))
# k = 0
# for e in M[i] :
# k += 1
# Line = " %2d " % (k)
# for pos in e[1] :
# Line += " [%d,%d]" % (pos[0],pos[1])
# WriteLog(out,Line)
return M
###
def NormCheck(Mask,Pos,Pos2) :
global BitMask
pos = Pos + Pos2
m = Mask
for i in range(len(Pos),len(pos)) :
for j in range(0,i) :
dx = pos[i][0] - pos[j][0]
dy = pos[i][1] - pos[j][1]
d2 = dx*dx + dy*dy
if m & BitMask[d2] : return [-1,[]]
m |= BitMask[d2]
return [m,pos]
###
def Join(M,A,B,C,D,E,out) :
if E == 0 :
me = 0L
Pe = []
else :
me = BitMask[2*5+2]
Pe = [[2,2]]
Cnt = 0
for [a,pa] in M[A] :
[ma,Pa] = NormCheck(me,Pe,pa)
for [b,pb] in M[B] :
pb2 = Shift(pb,3,0,1)
[mb,Pb] = NormCheck(ma,Pa,pb2)
if mb == -1 : continue
for [c,pc] in M[C] :
pc2 = Shift(pc,0,2,1)
[mc,Pc] = NormCheck(mb,Pb,pc2)
if mc == -1 : continue
for [d,pd] in M[D] :
pd2 = Shift(pd,2,3,0)
[md,Pd] = NormCheck(mc,Pc,pd2)
if md == -1 : continue
Cnt += DupCheck(Pd,out)
return Cnt
###
def Shift(Pos,dx,dy,t) :
if Pos == [] : return []
pos = []
for [x,y] in Pos :
if t == 0 : pos += [[x+dx,y+dy]]
else : pos += [[y+dx,x+dy]]
return pos
###
def DupCheck(Pos,out) :
global Ans,BitMask
V = BitMask[33]
for t in range(0,8) :
pos = []
v = 0L
for [x,y] in Pos :
if t & 0x01 : x = 4-x
if t & 0x02 : y = 4-y
if t & 0x04 :
w = x
x = y
y = w
pos += [[x,y]]
v |= BitMask[5*y+x]
V = min(v,V)
for ans in Ans :
if ans == V : return 0
Ans += [V]
printMap(out,len(Ans),V)
return 1
###
def Bits(K) :
w = K
c = 0
while w != 0 :
c += 1
w = w & (w-1)
return c
###
def printMap(out,Cnt,Map) :
Line ="\n%4d " % (Cnt)
WriteLog(out,Line)
C = ["○","●"]
map = Map
for i in range(0,5) :
Line = " "
for j in range(0,5) :
m = map & 0x01
map = map >> 1
Line += C[m]
WriteLog(out,Line)
###
def WriteLog(out,Line) :
print Line
out.write(Line+"\n")
out.flush()
7x7の解は、以下の1つ。
探索時間は、45秒。(Pentium4 1.4GHz)○○○○●○●
○○○○●○○
●○○○○○○
○○○○○○●
○○○○○○○
○●○○○○○
●○○○○○○
8x8の解は,存在しない。
探索時間は、約12分。
◆補足
『16個以上の石をバラバラに配置する解は存在しない』ことの補足説明です。
1.準備(用語の定義など)
(1)a、bを0以上の整数とし、自然数mが(a2+b2)で表すことができるとき、mをノルム数と呼ぶことにする。
また、その構成要素を[a,b]と表記する。
[a,b]の次数をmax(a,b)と定義する。
mの表記の中で次数が最小となる表記を既約表記とする。
ex. 25=[0,5]=[3,4]の場合、[3,4]が既約表記となる
5=[1,2]の場合は、(1つしか存在しないので)、[1,2]が既約表記となる
注:2つの石の間のX軸、Y軸の差分をそれぞれa,bとすると、[a,b]は、距離の2乗に対応する。
(2)L(N):NxNのパネルに配置できる2つの石の間の距離が異なるものの数とする。
L(N)は、次数(N−1)以下の既約表記の数に等しい。

N≦21については、添付ファイルを参照されたい。
(3)R(N):N個の石をバラバラに配置したとき、必要となる異なる距離の種類の数。
| R(N)= | N*(N−1) 2 | となる。 |
(4)δL(N) = L(N) − L(N-1) と定義する。
L(N)の定義から、L(N-1)からL(N)になることで増えるのは、
[0,N-1],[1,N-1],[2,N-1],... [N-1,N-1]のN個の中で既約表記となっているものだけである。
従って、δL(N)≦Nとなる。
(5)δR(N) = R(N) − R(N-1) と定義する。
(3)より、δR(N)=N−1となる。
以上より、N個の石をバラバラに配置できるためには、
L(N)≧R(N)であることが必要である。
もし、『N≧16の場合、L(N)<R(N)』が成立すれば、バラバラの配置の解は存在しない。
N=16では、この条件が成立しているので、
(添付のR(N),L(N)の計算結果を参照)
N>16で、δL(N)≦δR(N)が成立すれば、もとの命題も成り立つことになる。
2.命題 『N>16の時、δL(N)≦δR(N)が常に成り立つ』
(4)、(5)より、δL(N)≦N、δR(N)=N−1であるから、
δL(N)の中に既約表記でないものが1つでも含まれていれば、命題が成立することになる。
1)n = 5*k の場合(k>3)
[0,n] = [0,5*k]
= (5*k)2
= (3*k)2 + (4*k)2
= [3*k,4*k]
k>3では、[0,5*k]の次数は、[3*k,4*k]より大きいので、
[0,5*k]は既約表記ではない。
2)n = 5*k+1 の場合(k≧3)
[2,n] = [2,5*k+1]
= (5*k+1)2 + 22
= 25*k2 * 10*k + 5
= (3*k-1)2 + (4*k+2)2
= [3*k-1,4*k+2]
k≧3では、[2,5*k+1]の次数は、[3*k-1,4*k+2]より大きいので、
[2,5*k+1]は既約表記ではない。
3)n = 5*k+2 の場合(k≧3)
[1,n] = [1,5*k+2]
= (5*k+2)2 + 12
= 25*k2 * 20*k + 5
= (3*k+2)2 + (4*k+1)2
= [3*k+2,4*k+1]
k≧3では、[1,5*k+2]の次数は、[3*k+2,4*k+1]より大きいので、
[1,5*k+2]は既約表記ではない。
4)n = 5*k+3 の場合(k≧3)
[4,n] = [4,5*k+3]
= (5*k+3)2 + 42
= 25*k2 * 30*k + 25
= (3*k+5)2 + (4*k)2
= [3*k+5,4*k]
k≧3では、[4,5*k+3]の次数は、[3*k+5,4*k]より大きいので、
[4,5*k+3]は既約表記ではない。
5)n = 5*k+4 の場合(k≧3)
[2,n] = [2,5*k+4]
= (5*k+4)2 + 42
= 25*k2 * 40*k + 20
= (3*k+4)2 + (4*k+2)2
= [3*k+4,4*k+2]
k≧3では、[2,5*k+4]の次数は、[3*k+4,4*k+2]より大きいので、
[2,5*k+4]は既約表記ではない。
1)〜5)のいずれの場合も、命題は成り立っている。
従って、N≧16の場合、L(N)<R(N)が成り立つので、『16個以上の石をバラバラに配置する解は存在しない』ことになる。
◆福岡県 昼行灯 さんからの解答
【問題1】
思ったよりも難しいですね。
適当においてもなかなか正解が出ませんし、きれいな解法が思い浮かびません。
仕方が無いのでPGで解くと
5×5の場合 280パターン
6×6の場合 16パターンです。
5×5の場合
※番号と枠が対応してます。
| 01 | 02 | 03 | 04 | 05 |
| 06 | 07 | 08 | 09 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
01 02 05 12 24 01 02 05 14 24 01 02 08 10 25 01 02 08 16 25 01 02 08 21 24以下 省略
全結果はこちらです。
計280パターン
6×6の場合
| 01 | 02 | 03 | 04 | 05 | 06 |
| 07 | 08 | 09 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 |
01 02 10 24 33 36 01 03 06 22 29 35 01 03 17 19 30 36 01 04 06 21 26 32 01 04 13 27 35 36 01 07 18 20 34 36 01 11 12 16 19 31 01 13 22 29 30 31 02 08 15 31 34 36 03 06 18 28 31 32 04 06 14 24 25 31 05 06 09 19 31 34 05 11 16 31 33 36 06 07 08 15 24 36 06 12 13 23 31 33 06 18 21 25 26 36計16パターン
解答の追加です。
前回は全パターンをそのまま数えていましたが、90度回転及び裏表反転の同一パターンの組み合せが8パターンありますね。
検出された組み合わせを8で割ると以下のようになりました。マス目 組合せ
3×3 5
4×4 23
5×5 35
6×6 2
7×7 1
8×8 0
9×9 0
10×10 0
10×10の時点でプログラム(VB)の実行時間が7時間でしたので11×11は止めました。
6×6までは5秒程度7×7は1分程度ですが、それ以降は飛躍的に組合せのパターンが上がるので当然の結果ですが。
プログラムで解けば簡単ですが、理論的に考えようとすると・・解法が浮かびません。
他の人の解答に期待です。
ちなみに7×7の場合
| 01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 08 | 09 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 43 | 44 | 45 | 46 | 47 | 48 | 49 |
01 03 10 21 22 41 49 01 04 15 16 41 45 49 01 05 09 34 35 46 49 01 09 28 29 40 47 49 03 07 13 29 30 43 46 04 07 20 21 37 43 47 05 07 12 15 28 37 43 07 13 22 35 38 43 45です。
◆浜田 明巳 さんからの解答
いずれもエクセルのマクロで解いた.
N×N個(N=5,6)のマスの中からシラミつぶしでN個を選び,任意の2個間の距離の2乗を求める.
2乗にしたのは,コンピュータは近似値(切り捨て)なので,ルート計算を避ける為である.
それらの距離の2乗の中で1つでも等しいものがあれば,捨て去り,等しいものがなければ,それを答とし,表示する.
【問題1・おまけ1】
次の35通り.ただし対称解は除いてある.
もし対称解を含めるのなら8倍の280通り.
ちなみに8倍となるのは,上下対称,左右対称,右上がり対角線対称,右下がり対角線対称,90°回転,180°回転,270°回転の7種類が,1つの本質解と重複しているからである.11001
00000
01000
00000
00010
11001
00000
00010
00000
00010
11000
00101
00000
00000
00001
11000
00100
00000
10000
00001
11000
00100
00000
00000
10010
11000
00100
00000
00000
01001
11000
00100
00000
00000
00101
11000
00010
00000
00000
01010
11000
00001
00010
00000
00001
11000
00001
00000
00010
00001
11000
00000
10010
00001
00000
11000
00000
10000
00010
00100
11000
00000
10000
00010
00001
11000
00000
01000
10000
00001
11000
00000
00000
00100
10010
11000
00000
00000
00100
01001
11000
00000
00000
00010
01001
10110
00000
00000
00001
00100
10100
00100
00000
00000
10010
10100
00011
00000
00000
10000
10100
00010
00000
00001
10000
10100
00000
00001
00110
00000
10100
00000
00001
00010
00010
10100
00000
00000
10000
00110
10100
00000
00000
00110
00001
10100
00000
00000
00011
00100
10010
01000
00000
00000
00110
10010
00000
00000
01000
01010
10010
00000
00000
01000
00110
10001
01000
01000
00000
01000
10000
01001
00000
00011
00000
10000
01001
00000
00010
00010
01100
10000
00000
00101
00000
01100
00000
01000
00001
00010
01000
10000
00011
00000
00010
【問題2・おまけ2】
次の2通り.ただし対称解は除いてある.
もし対称解を含めるのなら8倍の16通り.
110000
000100
000000
000001
000000
001001
101001
000000
000000
000100
000010
000010
【参考】
ちなみにN=7の場合は次の1通りになる.
1010000
0010000
0000001
1000000
0000000
0000010
0000001
Option Explicit
Public N As Integer
Sub Macro1()
Dim a(6) As Integer
For N = 5 To 6
If N = 5 Then
Sheets("Sheet1").Select
Columns("B:F").Select
Else
Sheets("Sheet2").Select
Columns("B:G").Select
End If
Selection.ColumnWidth = 1.88
Selection.ClearContents
Cells(1, 1).Value = 0
Range("A1").Select
'
Call saiki(1, a())
Next N
End Sub
Sub saiki(ByVal i As Integer, ByRef a() As Integer)
Dim b(6, 6) As Integer
Dim x(1) As Integer
Dim y(1) As Integer
Dim d2(15) As Integer '15=6*5/2
Dim kosuu As Integer
Dim j1 As Integer
Dim j2 As Integer
Dim j3 As Integer
Dim j4 As Integer
Dim bb As Integer
Dim onaji As Integer
Dim chigau As Integer
Dim gyou As Integer
If i = 1 Then
a(1) = 1
Else
a(i) = a(i - 1) + 1
End If
While a(i) <= N * N - (N - i)
If i < N Then
Call saiki(i + 1, a())
Else
kosuu = 0
For j1 = 1 To N - 1
x(0) = f(a(j1), 0)
y(0) = f(a(j1), 1)
For j2 = j1 + 1 To N
x(1) = f(a(j2), 0)
y(1) = f(a(j2), 1)
kosuu = kosuu + 1
d2(kosuu) = (x(1) - x(0)) * (x(1) - x(0)) + (y(1) - y(0)) * (y(1) - y(0)) '距離の2乗
Next j2
Next j1
onaji = 0
j1 = 1
While onaji = 0 And j1 <= kosuu - 1
j2 = j1 + 1
While onaji = 0 And j2 <= kosuu
If d2(j1) = d2(j2) Then
onaji = 1
Else
j2 = j2 + 1
End If
Wend
j1 = j1 + (1 - onaji)
Wend
If onaji = 0 Then
For j1 = 1 To N
For j2 = 1 To N
b(j1, j2) = 0
Next j2
Next j1
For j1 = 1 To N
b(f(a(j1), 0), f(a(j1), 1)) = 1
Next j1
j1 = 1
While onaji = 0 And j1 <= 7
j2 = 1
While onaji = 0 And j2 <= Cells(1, 1).Value
gyou = j2 * (N + 1) - N
chigau = 0
j3 = 1
While chigau = 0 And j3 <= N
j4 = 1
While chigau = 0 And j4 <= N
Select Case j1
Case 1
bb = b(j3, N + 1 - j4) '上下対称
Case 2
bb = b(N + 1 - j3, j4) '左右対称
Case 3
bb = b(j4, j3) 'y=x対称
Case 4
bb = b(N + 1 - j4, N + 1 - j3) 'y=n+1-x対称
Case 5
bb = b(N + 1 - j4, j3) '90°回転
Case 6
bb = b(N + 1 - j3, N + 1 - j4) '180°回転
Case Else
bb = b(j4, N + 1 - j3) '270°回転
End Select
If Cells(gyou + j3 - 1, j4 + 1) <> bb Then
chigau = 1
Else
j4 = j4 + 1
End If
Wend
j3 = j3 + 1
Wend
If chigau = 0 Then
onaji = 1
Else
j2 = j2 + 1
End If
Wend
j1 = j1 + 1
Wend
If onaji = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = (N + 1) * Cells(1, 1).Value - N
For j1 = 1 To N
For j2 = 1 To N
Cells(gyou + j1 - 1, j2 + 1).Value = b(j1, j2)
Next j2
Next j1
End If
End If
End If
a(i) = a(i) + 1
Wend
End Sub
Private Function f(ByVal x As Integer, ByVal i As Integer) As Integer
If i = 0 Then
f = (x - 1) \ N + 1
Else
f = ((x - 1) Mod N) + 1
End If
End Function
◆東京都 明 さんからの解答
【問題1】●□□●□
●□□□□
□●□□□
□□□□□
□□□□●
左上隅を起点として、小さな距離の順に石を置いて行きます。
石を置いたら等距離の位置のマスを除去して、次の石を置ける位置を決定します。
このとき既に置いてある石と等距離にない位置に石を置くように注意します。
このような方法で容易に解が見つかりました。
【問題2】
【問題1】と同様な方法では解にたどりつけず、プログラムで下記2種類の基本解を得ました。No : 1
□□□□□●
□□□□□□
□□□□□●
□□●□□□
●●□□□□
□□□□□●
No : 2
□□□□□●
□□□□□●
●□□□□□
□□□□●□
□□□□□□
●□●□□□
【おまけ1】
プログラムにより、基本35種類を確認しました。
裏返し、回転を別ものとすれば280通りになります。
【おまけ2】
【問題2】の基本2種類。
裏返し、回転を別ものとすれば16通りになります。
なお、7×7のマス目で7個の石では基本解は次の1種類のみであることを確認しました。No : 1
□□□□□□●
□□□□□●□
□□□□□□□
●□□□□□□
□□□□□□●
□□●□□□□
●□●□□□□
8×8のマス目で8個の石ではプログラムの実行に時間がかかり過ぎ、完了ができませんでした。
石の配置の解が存在する限界を考察してみました。
| N×Nのマス目でN個の石では、石の距離の数は | N(N−1) 2 | です。 |
| 一方マスの行・列数の違いで距離の種類を数えると | N(N+1) 2 | −1。 |
行・列数が違っても距離が同じものがあるのでこの数をDとすると、
| マスの距離の種類は | N(N+1) 2 | −1−D。 |
従って、D≧Nでは石が配置できないことになります。
計算機でN=20まで確認しましたが
N≧16でD≧N、N≦15でD<Nです。
理論的にもN増加の割合よりもDの増加の割合が大きいことが証明できそうですので、
N≧16では解がないと予想できます。
(N=8も計算機のRUNの途中結果ですが、解がなさそうです。)
プログラムを参考で添付します。
(10進BASIC。同型を削除する仕掛けをしています。)
DECLARE EXTERNAL SUB zyun
DECLARE EXTERNAL SUB rever
DECLARE EXTERNAL SUB rotat
LET M=6
LET K=M*M
DIM N(K)
DIM NC(K)
DIM ND(K)
DIM NB(50,K)
DIM L((M-1)*M/2)
DIM X(M)
DIM Y(M)
LET COUNT=0
MAT N=ZER
FOR J=0 TO M-1
LET N(K-J)=1
NEXT J
DO
LET C=1
LET R=0
LET G=0
FOR J=1 TO K
IF N(J)=1 THEN
LET X(C)=R
LET Y(C)=G
LET C=C+1
END IF
LET R=MOD(R+1,M)
IF R=0 THEN LET G=G+1
NEXT J
CALL check
IF P=1 THEN
CALL paral
IF P=1 THEN
LET COUNT=COUNT+1
CALL print
FOR J=1 TO K
LET NB(COUNT,J)=N(J)
NEXT J
END IF
END IF
CALL zyun(K,EX,N)
LOOP UNTIL EX=0
PRINT "総数 : ";COUNT
STOP
SUB print
PRINT "No : ";COUNT
LET R=0
FOR J=1 TO K
IF N(J)=1 THEN PRINT "●"; ELSE PRINT "□";
LET R=MOD(R+1,M)
IF R=0 THEN PRINT
NEXT J
END SUB
SUB check
LET P=0
MAT L=ZER
LET C=1
FOR J=1 TO M-1
FOR I=J+1 TO M
LET B=(X(J)-X(I))^2+(Y(J)-Y(I))^2
FOR H=1 TO C
IF L(H)=B THEN EXIT SUB
NEXT H
LET L(C)=B
LET C=C+1
NEXT I
NEXT J
LET P=1
END SUB
SUB paral
LET P=1
IF COUNT=0 THEN EXIT SUB
LET P=0
FOR J=1 TO COUNT
MAT ND=N
FOR H=1 TO 3
CALL rotat(M,ND,NC)
LET CMP=1
FOR I=1 TO K
IF NB(J,I)<>NC(I) THEN
LET CMP=0
EXIT FOR
END IF
NEXT I
IF CMP=1 THEN EXIT SUB
MAT ND=NC
NEXT H
CALL rever(M,N,NC)
LET CMP=1
FOR I=1 TO K
IF NB(J,I)<>NC(I) THEN
LET CMP=0
EXIT FOR
END IF
NEXT I
IF CMP=1 THEN EXIT SUB
MAT ND=NC
FOR H=1 TO 3
CALL rotat(M,ND,NC)
LET CMP=1
FOR I=1 TO K
IF NB(J,I)<>NC(I) THEN
LET CMP=0
EXIT FOR
END IF
NEXT I
IF CMP=1 THEN EXIT SUB
MAT ND=NC
NEXT H
NEXT J
LET P=1
END SUB
END
!位置の回転
EXTERNAL SUB rotat(L,N(),M())
FOR X=0 TO L-1
FOR Y=0 TO L-1
LET XC=L-1-Y
LET YC=X
LET M(L*XC+YC+1)=N(L*X+Y+1)
NEXT Y
NEXT X
END SUB
!左右反転
EXTERNAL SUB rever(L,N(),M())
FOR X=0 TO L-1
FOR Y=0 TO L-1
LET YC=L-1-Y
LET M(L*X+YC+1)=N(L*X+Y+1)
NEXT Y
NEXT X
END SUB
!順列の変更
EXTERNAL SUB zyun(K,EX,N())
DECLARE EXTERNAL SUB seiretu
LET EX=0
LET J=1
DO
IF J>=K THEN EXIT DO
IF N(K-J)<N(K-J+1) THEN
CALL seiretu(J,K,N)
LET L=1
DO
IF N(K-J)>=N(K-J+L) THEN
LET L=L+1
ELSE
LET B=N(K-J)
LET N(K-J)=N(K-J+L)
LET N(K-J+L)=B
LET EX=1
EXIT DO
END IF
LOOP
EXIT DO
ELSE
LET J=J+1
END IF
LOOP
END SUB
!配列の整列
EXTERNAL SUB seiretu(J,K,N())
LET D=K-J+1
LET E=K
DO WHILE D<E
LET B=N(D)
LET N(D)=N(E)
LET N(E)=B
LET D=D+1
LET E=E-1
LOOP
END SUB◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
等。
左側解は上辺とその他の2群にわけて考えたものであるが、カットアンドトライというべきものでここへの詳述には値しない。
【問題2】
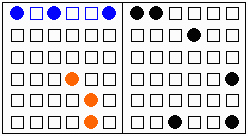
これも左側解は上辺とその他の2群にわけて考えたものである。
【おまけ】
PC探索による結果を表1に示す。
回転左右上下8対称で分類した数である。
なお、マスの巾数:N=9までは単純なシラミ潰しで探索し、
N=10〜15は表2の性質(Lの余裕が殆ど無い)を利用し、
外周探索範囲で一度ふるいを掛け、効率的に探索した。
表1 答え
![]()
マス巾数7は唯一解なので下記に示しておく。

マス巾数:N=8以上では存在しない。
∵ 少なくとも距離として NC2種類が必要である。
| マス上には距離として | (N+2)*(N-1) 2 | 種の可能性があり、 |
しかしNが大きくなると
A2+B2=C2+D2
の成立する組み合わせが N2の程度で存在するため、
N≧16では表2に示すように有効な距離の種類数L(N)が、NC2を下回り、
N≧16では一般に存在しないといえる。
なお、例えば
(4p+3q)2+(3p−4q)2=(5p)2+(5q)2
が任意の整数p、qにおいて恒等的に成立することを利用して
A2+B2=C2+D2
の成立する組み合わせがN2の程度であることを証明できる。
表2 L(N)とNC2

なお、N=15までの可否は表1に示したとおりである。
【PS】
明さんの解答から、最初の解答でL(N)の計算を間違っていることに気づき再計算&訂正しました。
さすがに前回のように数分では無理でしたが、最大数十分の計算時間で探索できました。
(CPU=500MHz)
◆ 問題へもどる
◆ 今週の問題へ