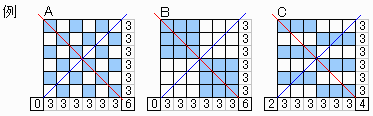
◆千葉県 菜花子 さんからの解答
最初に、縦、横の線上に3匹のカエルを配置する。

赤と青のそれぞれの対角線上に、3匹ずつ並ぶように入れ替える。
AとBの場合は、赤の線上の3匹を青の線上へ、
Cの場合は、赤の線上の1匹を青の線上へ移動させる。
【問題1】(Cの配列を使って)

◆浜田 明巳 さんからの解答
次のように答はたくさんあります.
エクセルのマクロで解きました.
0 0 0 1 1 1
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 1 0 0
1 0 1 0 1 0
1 1 1 0 0 0
0 0 0 1 1 1
0 0 0 1 1 1
1 0 1 0 1 0
1 1 0 1 0 0
1 1 1 0 0 0
0 1 1 0 0 1
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
0 1 0 1 0 1
1 0 1 0 1 0
1 1 1 0 0 0
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
1 0 0 1 1 0
1 1 1 0 0 0
0 1 1 0 0 1
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
1 1 0 1 0 0
0 0 1 0 1 1
1 1 1 0 0 0
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
1 1 0 1 0 0
1 1 1 0 0 0
0 0 1 0 1 1
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
1 1 1 0 0 0
1 0 0 1 1 0
0 1 1 0 0 1
0 0 0 1 1 1
0 0 0 1 1 1
1 1 1 0 0 0
1 1 1 0 0 0
1 0 1 0 1 0
0 1 0 1 0 1
0 0 0 1 1 1
0 0 1 0 1 1
0 1 1 0 0 1
1 1 0 1 0 0
1 0 0 1 1 0
1 1 1 0 0 0
0 0 0 1 1 1
0 0 1 0 1 1
0 1 1 0 0 1
1 1 0 1 0 0
1 0 1 0 1 0
1 1 0 1 0 0
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Columns("B:G").Select
Selection.ColumnWidth = 1.88: Selection.ClearContents
Cells(1, 1).Value = 0: Range("A1").Select
Dim a(6, 6) As Integer
Call saiki1(1, a())
End Sub
Sub saiki1(ByVal n As Integer, ByRef a() As Integer)
Call saiki2(n, a(), 1)
End Sub
Sub saiki2(ByVal n As Integer, ByRef a() As Integer, ByVal i As Integer)
Dim b(6, 6) As Integer, bb As Integer, wa As Integer
Dim dame As Integer, chigau As Integer, onaji As Integer
Dim gyou As Integer
Dim j1 As Integer, j2 As Integer, j3 As Integer, j4 As Integer
If i = 1 Then
a(n, 1) = 1
Else
a(n, i) = a(n, i - 1) + 1
End If
While a(n, i) <= 6 - (3 - i)
If i < 3 Then
Call saiki2(n, a(), i + 1)
Else
If n < 6 Then
Call saiki1(n + 1, a())
Else
For j1 = 1 To 6
For j2 = 1 To 6
b(j1, j2) = 1
Next j2
Next j1
For j1 = 1 To 6
For j2 = 1 To 3
b(j1, a(j1, j2)) = 0
Next j2
Next j1
'
dame = 0: j1 = 1
While dame = 0 And j1 <= 6 + 2
wa = 0
For j2 = 1 To 6
Select Case j1
Case 1 To 6: wa = wa + b(j2, j1) '縦チェック
Case 6 + 1: wa = wa + b(j2, j2) '右斜め下チェック
Case Else: wa = wa + b(j2, 7 - j2) '左斜め下チェック
End Select
Next j2
If wa <> 3 Then
dame = 1
Else
j1 = j1 + 1
End If
Wend
'
If dame = 0 Then
onaji = 0: j1 = 1
While onaji = 0 And j1 <= 7
j2 = 1
While onaji = 0 And j2 <= Cells(1, 1).Value
gyou = j2 * 7 - 6
chigau = 0: j3 = 1
While chigau = 0 And j3 <= 6
j4 = 1
While chigau = 0 And j4 <= 6
Select Case j1
Case 1: bb = b(j3, 7 - j4) '上下対称
Case 2: bb = b(7 - j3, j4) '左右対称
Case 3: bb = b(j4, j3) 'y=x対称
Case 4: bb = b(7 - j4, 7 - j3) 'y=7-x対称
Case 5: bb = b(7 - j4, j3) '90°回転
Case 6: bb = b(7 - j3, 7 - j4) '180°回転
Case Else: bb = b(j4, 7 - j3) '270°回転
End Select
If Cells(gyou + j3 - 1, j4) <> bb Then
chigau = 1
Else
j4 = j4 + 1
End If
Wend
j3 = j3 + 1
Wend
If chigau = 0 Then
onaji = 1
Else
j2 = j2 + 1
End If
Wend
j1 = j1 + 1
Wend
If onaji = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 7 - 6
For j1 = 1 To 6
For j2 = 1 To 6
Cells(gyou + j1 - 1, j2 + 1).Value = b(j1, j2)
Next j2
Next j1
End If
End If
End If
End If
a(n, i) = a(n, i) + 1
Wend
End Sub
◆東京都 JAVAKnight さんからの解答
【問題1】×,×,○,○,○,×,
○,×,×,○,×,○,
×,○,×,×,○,○,
○,×,○,○,×,×,
×,○,○,×,○,×,
○,○,×,×,×,○
は正解の一つである。
また、各行に三つずつの蛙を置く方法の総数は、
(6!/3!/(6-3)!)6=64000000通りなので、
この数だけ調べて問題の条件に合うものを調べると、
各行、各列と斜めの列に三つの蛙が並ぶ蛙の配置は、24032通りあることが分かる。