『今週の問題』

『今週の問題』第194回　解答

◆京都府の中学校２年生　pirochies さんからの解答

【問題１】

 1⇔ 7， 7⇔20，20⇔16，16⇔11，11⇔ 2，
 2⇔24， 3⇔10，10⇔23，23⇔14，14⇔18，
18⇔ 5， 4⇔19，19⇔ 9， 9⇔22， 6⇔12，
12⇔15，15⇔13，13⇔25，21⇔17，

の合計19回の動きで出来る。

【問題２】

理由「1番が入るところに7番がある、7番が入るところに20番がある、20番が入るところに16番がある」、、、を繰り返すと、「22番が入るところに1番がある」　と最初に戻ります。
これをループと考えました。

最初の状態で、ループは、

1-7-20-16-11-2-24　-1
3-10-23-14-18-5　-3
4-19-9-22　-4
6-12-15-13-25　-6
17-21　-17
8　-8

の6つがあります。

１番のループ(1,7,20,16,11,2,24)は、
1⇔ 7， 7⇔20，20⇔16，16⇔11，11⇔ 2， 2⇔24，
とやれば、１番のループに関係する数字がすべて正しい場所に入ります。
こうすると、７個のループに関係する数字が６回の操作で正しくなります。

ループの数字の位置関係を正しくするには、「ループに関係する数字の数－１」回操作すれば、正しくなることがわかります。

　そう考えると、２番のループは５回、３番のループは３回、４番のループは４回、５番のループは１回（６番のループは０回）の操作で位置関係がすべて正しくなります。

　計６つのループごとの操作をする回数の合計である
６＋５＋３＋４＋１＝１９回が、この問題の答えになります。

◆千葉県　菜花子さんからの解答

【問題１】

 1⇔ 7， 2⇔24， 3⇔10， 4⇔19， 5⇔10，
 6⇔12， 7⇔20， 9⇔22，10⇔23，11⇔24，
12⇔15，13⇔25，14⇔18，15⇔25，16⇔24，
17⇔21，18⇔23，19⇔22，20⇔24，

【問題２】

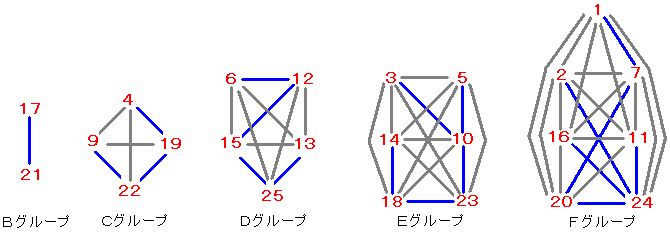
１～２５の数字のカードは、上記５つのグループに分けられる。

Ａグループ：〔８〕は入れ替えは不要・・・０回
Ｂグループ：２枚のカードの入れ替え・・・１回
Ｃグループ：４枚のカードの入れ替え・・・３回
Ｄグループ：５枚のカードの入れ替え・・・４回
Ｅグループ：６枚のカードの入れ替え・・・５回
Ｆグループ：７枚のカードの入れ替え・・・６回

したがって、１９回が最少回数である。

（青線の数が、２枚のカードを入れ替えた回数を示す。）

◆静岡県　medaka さんからの解答

【問題１】

最小回数は、以下の１９回

 1⇔ 7， 2⇔24， 3⇔10， 4⇔19， 5⇔10，
 6⇔12， 7⇔20， 9⇔22，10⇔23，11⇔24，
12⇔15，13⇔25，14⇔18，15⇔25，16⇔24，
17⇔21，18⇔23，19⇔22，20⇔24

【問題２】

（最小回数であることの説明）

ａ．問題の表記と用語の定義

問題の配置をパネル上の位置（上段）とその位置にある数字（下段）の組合せとして書き直すと以下のようになる。

位置 →  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
数字 →  7 24 10 19  3 12 20  8 22 23  2 15 25 18 13 11 21  5  9 16 17  4 14  1  6

これを、しりとりの手順（下段の数字－>上段の位置の数字）に従って列を並べ替える。

1  7 20 16 11  2 24 *  3 10 23 14 18  5 *  4 19  9 22 *  6 12 15 13 25 * 8 * 17 21
7 20 16 11  2 24  1 * 10 23 14 18  5  3 * 19  9 22  4 * 12 15 13 25  6 * 8 * 21 17

（＊はしりとりの完結する位置をわかりやすくするために挿入）　　

使用する用語を以下の様に定義する。

循環列　　　：　上記のしりとりが完結する列のセット

例えば　1 7 20 16 11 2 24 7 20 16 11 2 24 1

循環列の長さ：循環列を構成する列の数。上記の例の場合は、７になる。
単位循環列　：長さが１の循環列

問題の正規表現：問題を循環列に並べ替えた表記

問題の位数　：問題に含まれる循環列の数。
与えられた問題の場合は、６。
最終形では、すべて単位循環列となるので２５（＝列の数）となる。

ｂ．交換操作と循環列との関係

パネル上の２つの数字を交換する操作を循環列に着目して見ると、
２つの循環列に跨る交換（例えば１と１０の交換）と
１つの循環列の中に閉じた交換（例えば７と２０の交換）
にわけることができる。

１と１０の交換のように２つの循環列に跨る交換をする場合は、以下のようになり、

 1  7 20 16 11  2 24   3 10 23 14 18 5 *
 7 20 16 11  2 24 10   1 23 14 18  5 3 *

これを整理すると、１つの循環列になっていることがわかる。

1  7 20 16 11  2 24 10 23 14 18 5 3 *
7 20 16 11  2 24 10 23 14 18  5 3 1 *

すなわち、２つの循環列に跨る交換は、２つの循環列を１つの循環列に連結する作用があり、問題の位数は１つ減少する。

次に７と２０の交換のように１つの循環列の中に閉じた交換の場合は、以下のようになり、

  1  7 20 16 11  2 24 *
 20  7 16 11  2 24  1 *

これを整理すると、２つの循環列に分割されていることがわかる。

7 *   1 20 16 11  2 24 *
7 *  20 16 11  2 24  1 *

２０と１１の交換の場合も、同様に、２つの循環列に分割される。

1  7 20 16 11  2 24 *   -->  1  7 11  2 24 *  20 26 *
7 11 16 20  2 24  1 *        7 11  2 24  1 *  26 20 *

以上から、１つの循環列の中に閉じた交換は、１つの循環列を２つの循環列に分割する作用があり、問題の位数は１つ増加する。

ｃ．最小回数となる手順の条件

以上の考察より、

(1)与えられた問題の位数（＝６）＜　最終形の位数（＝２５）であるから、『位数が増加する手順を常に選択する方法』が最小回数となる手順である

(2)１回の交換操作では、位数は１つしか増加しないので、
本問題の場合、２５－６＝１９回の交換が最小回数となる

(1),(2)をまとめると、『常に１つの循環列の中に閉じた交換を続ける』ことが最小回数の１９回となる手順である。
そして、その最も簡単な手順が、問題１の解答で示した『１から順番に所定の位置にない数字を交換により所定の位置に戻していく』という方法である。

【問題３】

最小回数となる手順の数は、
４２５，９３５，２５０，５３５，６７４，８８０，０００　通り

（求め方）

ａ．準備

長さがN1,N2,...,Nmのｍ個の循環列で構成される問題を
最小回数で解く手順の数をＲ（N1,N2,...,Nm）とする。
Ｒ（N1,N2,...,Nm）は、以下の関係が成り立つ。

１）　Ｒ（１）　＝　０

２）　Ｒ（２）　＝　１

３）Ｒ（Ｎ）＝Ｎ＊｛Ｒ(1,N-1)＋Ｒ(2,N-2)＋ ... ＋Ｒ(s,N-s)＊δ
2 ｝

ただし、
δ　＝　０　　　Ｎが奇数のとき
δ　＝　１　　　Ｎは偶数のとき

４）　Ｒ(N1,N2,...,N[k-1],1，N[k+1]，...，Nm）＝Ｒ(N1,N2,...,N[k-1],N[k+1]，...，Nm）
（長さ１の循環列は、無操作なので除外してよい）

５）　Nk ＞1 のとき　（k=1,2,...,m）

Ｒ（N1,N2,...,Nm）＝ (N1 + N2 + ... + Nm - ｍ)！
(N1-1)！＊(N2-1)！＊ ... ＊(Nm-1)！＊Ｒ(1)＊Ｒ(2)＊ ... ＊Ｒ(Nm)

１），２），４）は自明。
３），５）については、補足１，２で説明する。

ｂ．最小回数で解く手順の数

与えられた問題は、Ｒ（１，２，４，５，６，７）に該当する。
まず、Ｒ（３）～Ｒ（７）を１）～５）を使って、順次求めていく。

Ｒ（３）　＝　３＊｛Ｒ（１，２）｝　＝　３＊Ｒ（２）　＝　３

次に、Ｒ（４）を求めるために必要なＲ（２，２）を求めると

　Ｒ（２，２）
＝（２＋２－２）！
（２－１）！＊（２－１）！＊Ｒ（２）＊Ｒ（２）

＝２！
１！＊１！＊１＊１

＝　２

　Ｒ（４）
＝４＊｛Ｒ(1,3)＋Ｒ(2,2)
２｝

＝４＊｛Ｒ(3)＋Ｒ(2,2)
２｝

＝４＊(３＋２
２ )

＝　１６

同様にして、Ｒ(5)＝１２５、Ｒ(6)＝１２９６、Ｒ(7)＝１６８０７を得る。

最後に、
　Ｒ（１，２，４，５，６，７）
＝Ｒ（２，４，５，６，７）

＝（2＋4＋5＋6＋7－5）！
（2-1）！＊（4-1）！（5-1）！＊（6-1）！＊（7-1）！＊Ｒ(2)＊Ｒ(4)＊Ｒ(5)＊Ｒ(6)＊Ｒ(7)

＝１９！
３！＊４！＊５！＊６！＊１６＊１２５＊１２９６＊１６８０７
＝４２５，９３５，２５０，５３５，６７４，８８０，０００

この膨大な数がもとめる答えである。

補足１　３）の説明

長さｎの循環列の構成要素を（A1,A2,,,,An)とし、
これを長さｓと（ｎ－ｓ）の２つの循環列に分ける場合を考える。
（ただし、ｓ≦ｎ-ｓ)

ｓ＜ｎ－ｓの場合、長さｓの循環列の選び方は、以下のｎ通り。

(A1,A2, ... ,As) 　(A2,A3,...,A[s+1])　 ...　 (An,A1,...,A[s-1])

また、長さｓと（ｎ－ｓ）の２つの循環列の問題を解く手順の数は
Ｒ(ｓ，ｎ－ｓ)通りであるから
全体では、ｎ＊Ｒ(ｓ，ｎ－ｓ)通りとなる。

ｓ＝ｎ－ｓの場合（ｎは偶数，ｓ＝ｎ
２）、
長さｓの循環列の選び方は、以下のｎ
２通り。

注：(A1,A2, ... ,As) と（A[n/2+1],...,An) は同じ分割となっているため、半分になる

(A1,A2, ... ,As) (A2,A3,...,A[s+1]) ... (A[n/2],...,A[n-1])

また、長さｎ
２の２つの循環列の問題を解く手順の数は
Ｒ（ｎ
２，ｎ
２）通りであるから

全体では、ｎ
２＊Ｒ（ｎ
２，ｎ
２）通りとなる。

ｓは、１～ｎ
２の範囲で任意の整数値をとることができるので、

　Ｒ（ｎ）
＝ｎ＊Ｒ（１，ｎ－１）＋ｎ＊Ｒ（２，ｎ－２）＋．．．＋ｎ
２＊Ｒ（ｎ
２，ｎ
２）*δ

＝ｎ＊｛　Ｒ（１，ｎ－１）＋Ｒ（２，ｎ－２）＋．．．＋Ｒ（ｎ
２，ｎ
２）*δ／２　｝

但し、
δ＝０　　ｎが奇数のとき
δ＝１　　ｎが偶数のとき

補足２

５）の説明

２つの循環列ａ、ｂの長さをｎ、ｍとし、ａ、ｂを単独で解くて手順をそれぞれ

A1,A2,...,A[n-1]　　B1,B2,...,B[m-1]とする。

この手順の中からＡｉ，Ｂｊのいずれかを順番に取り出して並べると、ａ，ｂを合わせて解く手順となる。

例えば、A1,A2,...,A[n-1],B1,B2,...,B[m-1]やA1,B1,A2,B2,...A[-1]B[m-1]など
Ａi，Ｂjの並べ方は、ａ、ｂの中からａをｎ－１個、ｂをｍ－１個取り出す順列の数となるので

(ｎ＋ｍ－２)！
(ｎ－１)！＊(ｍ－１)！通りとなる。

また、ａ，ｂを単独で解く手順の数は、それぞれＲ（ｎ），Ｒ（ｍ）通りであるから、全体では、

Ｒ(ｎ，ｍ)＝ (ｎ＋ｍ－２)！
(ｎ－１)！＊(ｍ－１)！＊Ｒ（ｎ）＊Ｒ（ｍ）
となる。

一般の場合、ｍ個の循環列の長さをＮ１，Ｎ２，．．．，Ｎｍとすると

Ｒ(N1,N2,...,Nm)＝ (N1 + N2 + ... + Nm - ｍ)！
(N1-1)！＊(N2-1)！＊ ... ＊(Nm-1)！＊Ｒ(1)＊Ｒ(2)＊ ... ＊Ｒ(Nm)
となる。

補足３

Ｒ（ｎ）の一般式の予測

Ｒ（３）～Ｒ（７）の値は、３¹，４²，６⁴，７⁵となっているので、一般式として

Ｒ（ｎ）　＝　ｎ^ｎ－２が予測される。
しかし、証明を試みたが力及ばず、断念した。
回答者の中にこの証明があることを楽しみにしています。

◆東京都　明さんからの解答

【問題１】

 1⇔ 7， 2⇔24， 3⇔10， 4⇔19， 5⇔10，
 6⇔12， 7⇔20， 9⇔22，10⇔23，11⇔24，
12⇔15，13⇔25，14⇔18，15⇔25，16⇔24，
17⇔21，18⇔23，19⇔22，20⇔24，

【問題２】

マスの任意の目から始めて、その目にあるカードの数字を記録し、次にその数字の入るべき目に移り、そのカードの数字を記録します。
以下、同じことを繰り返すと、必ず最初に始めた目に戻り、結果として、数字の数珠つながりができます。

【問題】の場合は、下記のような６個の数珠ができます。

始めからあるべき位置にあるカード（この場合８）も１個の数珠として扱うこととします。

7→20→16→11→2→24→1
↑  　　　　　　　　　↓
　←―――――――――
10→23→14→18→5→3
↑　　　　　　　　 ↓
　←――――――――
19→9→22→4
↑　　　　 ↓
　←――――
12→15→13→25→6
↑  　　　　　　↓
　←――――――
 →8→
↑   ↓
 ←―
21→17
↑   ↓
 ←―

２枚のカードを交換したとき、この数珠がどのように変化するかを調べます。

（１）１個の数珠の中でカードを交換する場合。

例として、Ａ，Ｂ，Ｃ，Ｄ，Ｅのカードの数珠を考えます。

Ａ→Ｂ→Ｃ→Ｄ→Ｅ
↑  　　　　　　↓
　←――――――

ＢとＤを入れ替えると、下記のように２つの数珠に分かれます。

Ａ→Ｄ→Ｅ
↑　　  ↓
　←――
Ｃ→Ｂ
↑  ↓
　←

この状況をＲ(5)→Ｒ(3)＋Ｒ(2)と表すことにします。

数珠の中で隣あうカードを交換するとＲ(5)→Ｒ(4)＋Ｒ(1)となることが確かめられます。

Ｒ(1)は単一カードの数珠で、カードがあるべき位置に配置されていることを示します。

順に隣あうカードを交換して行くと、

Ｒ(5)→Ｒ(4)＋Ｒ(1)→Ｒ(3)＋2・Ｒ(1)→Ｒ(2)＋3・Ｒ(1)→5・Ｒ(1)
（ここで2・Ｒ(1)はＲ(1)＋Ｒ(1)を示す。以下同様）

よって、５枚のカードの数珠は最大でも４回でカードを正しい位置へ戻せます。

ここで、Ｒ(n)に数値n-1を対応させ、
これをＮＲ(n)＝n-1と表記することにします。

以上のように決めると、同一の数珠の中の任意の２枚カードを交換した場合、
Ｒ(n)→Ｒ(j)＋Ｒ(k)　(ｊ＋k＝n)となるとき、
ＮＲ(n)＝ＮＲ(j)＋ＮＲ(k)＋1　となります。
(n－1＝(j-1)＋(k-1)＋1より明らか)　

したがって、同一の数珠の中の２枚のカードの交換をＰ回続けたとき、
Ｒ(n)→Ｒ(j1)＋Ｒ(j2)＋・・・・＋Ｒ(ｊp)とすると
ＮＲ(n)＝ＮＲ(j1)＋ＮＲ(j2)＋・・・・＋ＮＲ(jp)＋Ｐとなります。

同一数珠内での交換をくりかえすと、いずれすべてのjq＝1となり、
よって、すべてのＮＲ(jq)＝0となります。

したがって、このときの交換回数Ｐとの間でＮＲ(n)＝Ｐが成り立ちます。

以上により、同一の数珠内でのカードの交換を続ければ、交換をどのようにしても、n－1回ですべてのカードが正しい位置に配置されることが判りました。

（２）異なった数珠の間でカードを交換する場合。

例として下記の長さが２と３の２個の数珠のＢとＤを交換すると、長さが５の数珠ができます。

Ａ→Ｂ→Ｃ
↑　　  ↓
　←――
Ｄ→Ｅ
↑  ↓
　←
Ａ→Ｄ→Ｅ→Ｂ→Ｃ
↑  　　　　　　↓
　←――――――

結果ＮＲ(5)＝ＮＲ(3)＋ＮＲ(2)+1となり、Ｒ(5)からカードの交換を進めても、元のＲ(3)＋Ｒ(2)の数珠から同一数珠内で交換を進めた場合より手数が多くなってしまいます。

これを一般化すりことにより、異なった数珠間でのカード交換は手数が多くなることを示せます。

（１）、（２）により、最短の手数でカードをあるべき位置に配置するための方法は、同一数珠内でカードを交換することであり、カードの数をＣ、数珠の数をＮとすると、最短手数はＣ－Ｎとなります。

カードを最短手数で正しい位置に配置するための判り易い方法のひとつは、任意の目にあるカードが、あるべき数字と異なっているとき、その目のカードとあるべき数字のカードを交換することです。

この方法は同一数珠内でのカードの交換を保証しますので、自動的に最短手数でカードを正しい位置に配置できます。

【問題３】

Ｒ(j1),Ｒ(j2)・・・,Ｒ(jq)　（n＝j1＋j2＋・・・＋jq)の数珠の最小回数の方法の数を
それぞれＷＲ(j1),ＷＲ(j2)・・,ＷＲ(jq)とすると、すべての場合の数は

(n-q)！
(j1-1)！・(j2-1)！・・・(jq-1)！・ＷＲ(j1)・ＷＲ(j2)・・・ＷＲ(jq)

により計算できます。

特に数珠が２個の場合は、
_n-2C_j-1・ＷＲ(j)・ＷＲ(n-j)で表すことができます。

ＷＲ(n)を求めるために漸化式を利用します。

Ｒ(n)の数珠の中の１つのカードに着目すると、このカードと交換できるカードはn-1枚で交換した時の数珠は次のとおりとなります。

Ｒ(n-1)＋Ｒ(1)，Ｒ(n-2)＋Ｒ(2)，・・，Ｒ(2)＋Ｒ(n-2)，Ｒ(1)＋Ｒ(n-1)

これらの最小回数の方法の合計Ｋは以下のとおりです。

Ｋ＝_n-2C₀・ＷＲ(n-1)・ＷＲ(1)＋_n-2C₁・ＷＲ(n-2)・ＷＲ(2)＋・・・＋_n-2C_n-3・ＷＲ(2)・ＷＲ(n-2)＋_n-2C_n-2・ＷＲ(1)・ＷＲ(n-1)

着目するカードはn枚あり、すべてのカードにわたってＫを加算したとき、同じカードの組み合わせが２回でることより、

ＷＲ(n)＝

n・Ｋ

　となります。

ＷＲ(2)＝1ですが、Ｋの式を成立させるため、ＷＲ(1)＝1とします。

以上により、ＷＲ(3)以降が順に求められます。

ＷＲ(25)まで数値計算した結果は以下のとおりです。
（10進BASICの1000桁モードを使用）

WR( 1)=  1 
WR( 2)=  1 
WR( 3)=  3 
WR( 4)=  16 
WR( 5)=  125 
WR( 6)=  1296 
WR( 7)=  16807 
WR( 8)=  262144 
WR( 9)=  4782969 
WR(10)=  100000000 
WR(11)=  2357947691 
WR(12)=  61917364224 
WR(13)=  1792160394037 
WR(14)=  56693912375296 
WR(15)=  1946195068359375 
WR(16)=  72057594037927936 
WR(17)=  2862423051509815793 
WR(18)=  121439531096594251776 
WR(19)=  5480386857784802185939 
WR(20)=  262144000000000000000000 
WR(21)=  13248496640331026125580781 
WR(22)=  705429498686404044207947776 
WR(23)=  39471584120695485887249589623 
WR(24)=  2315513501476187716057433112576 
WR(25)=  142108547152020037174224853515625

【問題】ではn＝25、j1＝7，j2＝6，j3＝5，j4＝4，j5＝2，j6＝1ですので、最小回数の場合の数は、以下のとおりとなります。

19!

6!・5!・4!・3!・1!・0!

・WR(7)・WR(6)・WR(5)・WR(4)・WR(2)・WR(1)

＝425935250535674880000

参考にWRを求めるプログラムを添付します。

DECLARE EXTERNAL FUNCTION comb
OPTION ARITHMETIC DECIMAL_HIGH
LET N=25
DIM C(N)
LET C(1)=1
LET C(2)=1
PRINT "WR( 1)= ";C(1)
PRINT "WR( 2)= ";C(2)
FOR J=3 TO N
   LET SUM=0
   FOR K=1 TO J-1
      LET SUM=SUM+comb(J-2,K-1)*C(K)*C(J-K)
   NEXT K
   LET C(J)=J*SUM/2
   PRINT "WR(";
   PRINT USING"##":J;
   PRINT")= ";C(J)
NEXT J

END

EXTERNAL FUNCTION comb(N,K)
OPTION ARITHMETIC DECIMAL_HIGH
LET comb=1
IF K=0 OR K=N THEN EXIT FUNCTION
LET C=1
FOR I=1 TO N-K
   LET C=C*(K+I)/I
NEXT I
LET comb=C
END FUNCTION

◆愛知県　Y.M.Ojisan さんからの解答

【問題１】　１９回

21⇔17， 1⇔ 7， 7⇔24， 7⇔ 2， 7⇔11，
 7⇔16， 7⇔20， 3⇔ 5， 3⇔18， 3⇔14，
 3⇔23， 3⇔10， 4⇔19，19⇔ 9， 9⇔22，
25⇔13，25⇔15，25⇔12，25⇔ 6，

【問題２】

巡回置換表現すると
(8)(21,17)(7,1,24,2,11,16,20)(10,23,14,18,5,3)(4,19,9,2)(6,12,15,13,25)
の６個に分解できる。

よって２５－６回である。

∵巡回置換間の互換をしたら、グループの数が減るので得策ではない。

２要素なら１回、３要素なら２回は明らかである。

今、ｎ要素ではn-1回必要とする。
巡回置換の一箇所を互換すると、結果は１要素が正しい位置で残りがn-1要素の巡回置換となるか、２個のn-1要素以下の巡回置換になる。
よって何れの場合も合計n-1回の互換が必要である。

【問題３】

425935250535674880000 とおり。

(8)と(21,17) は内部では１とおりである。
(21,17)互換の順序位置は19とおりである。

要素３個の巡回置換(a,b,c)の場合は内部では３通りであり、
その２個の互換の順序位置は白紙状態では　₁₉Ｃ₂ である。

f(n)を　ｎ個の要素の巡回置換をn-1個の互換の積での表現する場合の数とするとき
f(1)=1 f(2)=1 f(3)=3　であり、一般には下記である。

即ち、最初の互換で巡回置換は２個の巡回置換に分けられる。
分け方は１個とｎ－１個からｎ－１個と１個までのｎ－１種あり、それぞれ位置はｎとおりある。
ただし全て２重に数えており、下記となる。

2*f(n)
n = f(1)*f(n-1)+f(2)*f(n-2)*_n-2C₁+f(3)*f(n-3) *_n-2C₂+……+f(n-1)*f(1) *_n-2C_n-2

よって

f(4)=2*(1*3+1*1+3*1)=16=4²
f(5)=5/2*(1*16+1*3*3+3*1*3+16*1)=125=5³

f(6)=3*(1*125+1*16*4+3*3*6+16*1*4+125*1)=1296=6⁴
f(7)=7/2*(1*1296+1*125*5+3*16*10+16*3*10+125*1*5+1296*1)=16807=7⁵

（一般に　f(n)=n^n-2　である。証明略）

問題の６種の巡回置換の要素の数は　１、２、４、５、６、７である。
よって答えは

　f(1)*₁₉C₁*f(2)*₁₈C₃*f(4)*₁₅C₄*f(5)*₁₁C₅*f(6)*₆C₆*f(7)
＝19!*16*125*1296*16807/(3!*4!*5!*6!)
＝ 19!*16*125*1296*16807
3!*4!*5!*6!
＝425935250535674880000

である。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる

『今週の問題』第194回 解答

『今週の問題』第194回　解答