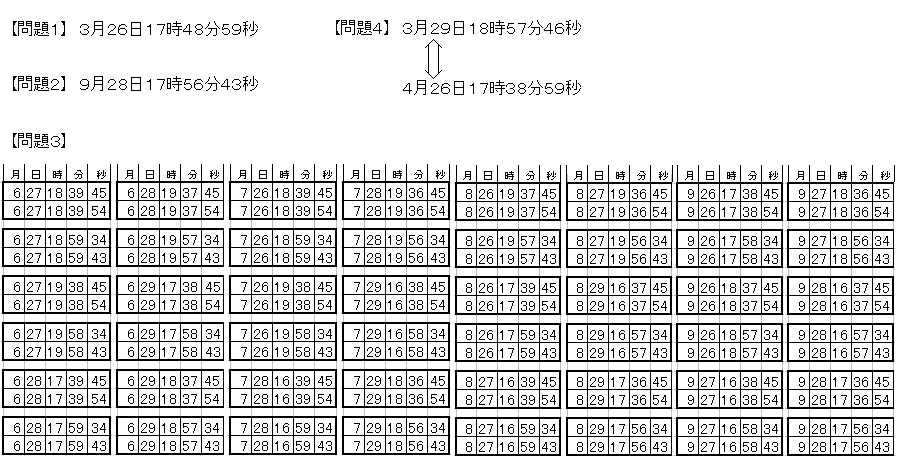
◆東京都 明 さんからの解答
【問題1】
3月26日 17:48:59
【問題2】
9月28日 17:56:43
【問題3】
下記の間です。
(他合わせて総計48点あるようです。)
6月27日 18:39:54
6月27日 18:39:45
【問題4】
下記の間です。
3月29日 18:57:46
4月26日 17:38:59
問題1、2は筆算レベルで確認できましたが、問題3は最小か確信の持てない予想レベルまでで、問題4に至っては面倒なので
最後に計算機のご厄介になりました。
以下にプログラムを添付します。(10進BASIC)
DECLARE EXTERNAL SUB zyun
REM 数値列データ
DATA 1,2,3,4,5,6,7,8,9
DIM N(9) ! ディジタル時計数列
MAT READ N
LET PMT=3 ! 前データ 月
LET PD=1 ! 前データ 日
LET PT=0 ! 前データ 時
LET PM=0 ! 前データ 分
LET PS=0 ! 前データ 秒
LET MSP=0 ! 最大時間差
LET LSP=9 ! 最小時間差(予想)
LET MINC=0 ! 最小時間差個数
LET COUT=0 ! 適合時刻個数
DO
CALL check
CALL zyun(9,EX,N)
LOOP UNTIL EX=0
PRINT "最大時間差 ";MSP;"秒"
PRINT "最小時間差 ";LSP;"秒"
PRINT "適合時刻個数 ";COUT
PRINT "最小時間差個数 ";MINC
PRINT "END"
SUB check
LET MT=N(1) ! 月の設定
REM 10月以上は条件に適合せず
SELECT CASE MT
CASE 1,3,5,7,8
LET DM=31
CASE 4,6,9,11
LET DM=30
CASE 2
LET DM=29 ! 閏年条件
END SELECT
LET D=10*N(2)+N(3)
IF D>DM THEN EXIT SUB ! 日の条件
IF N(4)>2 THEN EXIT SUB ! 時の条件
IF N(4)=2 AND N(5)>3 THEN EXIT SUB
IF N(6)>5 OR N(8)>5 THEN EXIT SUB ! 分、秒の条件
LET T=10*N(4)+N(5) ! 時の設定
LET M=10*N(6)+N(7) ! 分の設定
LET S=10*N(8)+N(9) ! 秒の設定
LET SP=24*3600*(D-PD+PDM*(MT-PMT))+3600*(T-PT)+60*(M-PM)+S-PS
IF SP>=MSP THEN LET MSP=SP ! 最大時間差の判定
LET PDM=DM
LET PMT=MT
LET PD=D
LET PT=T
LET PM=M
LET PS=S
LET COUT=COUT+1
PRINT MT;"月";D;"日 ";
PRINT T;":";M;":";S,SP;
IF SP<=LSP THEN ! 最小時間差の判定
PRINT "(MIN)"
LET MINC=MINC+1
ELSE
PRINT
END IF
END SUB
END
!順列の変更
EXTERNAL SUB zyun(K,EX,N())
DECLARE EXTERNAL SUB seiretu
LET EX=0
LET J=1
DO
IF J>=K THEN EXIT DO
IF N(K-J)<N(K-J+1) THEN
CALL seiretu(J,K,N)
LET L=1
DO
IF N(K-J)>=N(K-J+L) THEN
LET L=L+1
ELSE
LET B=N(K-J)
LET N(K-J)=N(K-J+L)
LET N(K-J+L)=B
LET EX=1
EXIT DO
END IF
LOOP
EXIT DO
ELSE
LET J=J+1
END IF
LOOP
END SUB
!配列の整列
EXTERNAL SUB seiretu(J,K,N())
LET D=K-J+1
LET E=K
DO WHILE D<E
LET B=N(D)
LET N(D)=N(E)
LET N(E)=B
LET D=D+1
LET E=E-1
LOOP
END SUB◆大阪府 SIN-K さんからの解答
【問題1】
3月26日17時48分59秒
【問題2】
9月28日17時56分43秒
【問題3】
6月27日18時59分34秒と6月27日18時59分43秒などの9秒差が計48通り
【問題4】
3月29日18時57分46秒と4月26日17時38分59秒の27日22時間41分13秒差
K−時刻は1から9までの数を1文字ずつ使用する為、月・日・時・分・秒の内どれか1つが1桁になるわけですが、月を2桁にした場合、10月は0が使えない為不可、11月は1を2回使用している為不可、12月はどのような組み合わせでも日と時の両方が1桁になってしまう為不可、よって、月が1桁になり、○月○○日○○時○○分○○秒という形になります。
K−時刻をA月BC日DE時FG分HI秒と置きます。
B=1と置くと、D=2、E=3となり、FとHが4または5になり、AとCとGとIが6または7または8または9になります。
この場合、6月から9月となります。
B=2と置くと、D=1となり、FとHが3または4または5になり、AとCとEとGとIが「FとHに使われなかった3または4または5の数」または6または7または8または9になります。
この場合、3月から9月となります。
1年の内で最初のK−時刻は3月となるのでA=3となり、B=2、D=1となり、F、Hの順に小さい数を入れる為F=4、H=5となり、C、E、G、Iの順に小さい数を入れる為C=6、E=7、G=8、I=9となります。
よって問題1は3月26日17時48分59秒となります。
1年の内で最後のK−時刻は9月となるのでA=9となり、B、Cの順に大きい数を入れる為B=2、D=1となり、F、Hの順に大きい数を入れる為F=5、H=4となり、C、E、G、Iの順に大きい数を入れる為C=8、E=7、G=6、I=3となります。
よって問題2は9月28日17時56分43秒となります。
34秒または45秒の時、月・日・時・分を変えずにHの数とIの数を入れ替れる為、その差が9秒になる。
なお、35秒の場合はその差が18秒になるので不可である。
またその組み合わせは、
34秒の時、B=2、D=1、F=5となり、AとCとEとGに6または7または8または9が入るので
4×3×2×1=24通り、
45秒の時、B=2、D=1、F=3となり、AとCとEとGに6または7または8または9が入るので
4×3×2×1=24通りの計48通りになる。
途中にK−時刻の無い最も離れた2つのK−時刻について。
2つのK−時刻が同じ月である場合、K−時刻となる16日から29日の内、最も離れている日が19日から23日の約4日間である。
2つのK−時刻が違う月である場合、その月の一番最後のK−時刻からその次の月の一番最初のK−時刻となる。
3月は3月29日から4月26日、4月は4月29日から5月26日、5月は5月29日から6月17日、6月は6月29日から7月16日、7月は7月29日から8月16日、8月は8月29日から9月16日となる。
この中で最も離れているのは3月29日18時57分46秒と4月26日17時38分59秒であり、その差は27日22時間41分13秒である。
◆栃木県の中学校2年生 大上佐中松 さんからの解答
全体を通して言える事として、k−時刻になるのは 1〜9の9個の数なので
○月○○日○○時○○分○○秒…(1)
又は
○○月○日○○時○○分○○秒…(2)
のどちらかである。
しかし、(2)の場合、月は10か11か12だが、0は使えないので10はありえない。
11は、同じ数を2回使っているのでありえない。
12は、ここで使うと時の十の位で使える数がなくなってしまうのでありえない。
だから、考えるのは、(1)の状態だけでよいことになる。
さらに考えられることとして、時の十の位には1か2しか入らない。
ただし、2の場合、時の一の位は1〜3しか入らなくなってしまう。
また、日の十の位は1〜3が入ると考えるが、3の場合、日の一の位は1しか入らない。
だから、時の十の位は2になるが、すでに1,2,3を使ってしまったので、前述のことから一の位に入れる数がなくなってしまうので、日の十の位も1か2しか入らない。
また、分と秒の十の位は1〜5しか入らない。
【問題1】
まず、日と時の十の位は1か2である。
従って、最初のk−時刻になる可能性があるのは3月。
そうすると、3月◎○日●○時○○分○○秒(◎●は1か2のどちらか)になる。
●が2の場合、時の一の位に、入れる数がないので●は1、従って◎は2となる。
つまり、3月2○日1○時○○分○○秒である。
残りは、分、秒の十の位を考えながら、数を入れると
3月26日17時48分59秒 となる。
【問題2】
最後のk−時刻になるになる可能性があるのは9月。
また、月、時の十の位を考えると、9月2○日1○時○○分○○秒
残りは、分、秒の十の位を考えながら、数を入れると
9月28日17時56分43秒となる。
【問題3】
秒の十の位と一の位の入れ替えができるところが近い2つのk−時刻となる。
入れ替えができる数は1〜5であるが、1と2は月、時の十の位で使うので3,4,5の3つから秒を作れば良い。
連続する数同士ならば、差は9秒であり、3と4でも4と5でもかまわないが、4と5で考えた。
すると ○月◎○日●○時○○分45秒 と ○月◎○日●○時○○分54秒
(◎●は1か2のどちらか)
適当に数を入れればできるので
9月26日17時38分45秒 と 9月26日17時38分54秒 とした。
【問題4】
はなれたk−時刻を作るには、日の十の位が1と2しか入らないので、最もはなれるのは、ある月の最後のk−時刻から次の月の最初のk−時刻である。
そこで、普通に考えれば、
○月2○日1○時○○分○○秒 から (○+1)月1○日2○時○○分○○秒
の組み合わせになるはずである。
ここで、次の月の最初のk−時刻に注目すると、時の十の位が2なので十の1の位は3になるはずである。
すると、月の最初のk−時刻は ○月1○日23時○○分○○秒となる。
ところが、そうすることによって、分と秒の十の位が4と5しか入れられなくなってしまう。
すると、4月と5月ではk−時刻を作ることができなくなってしまう。
従って、4月と5月の月の最初のk−時刻は○月2○日1○時○○分○○秒となる。
以上のことから、はなれたk−時刻は、
3月最後から4月最初…A、または、4月最後から5月最初…B
のどちらかである。
Aの場合、3月29日18時57分46秒から4月26日17時38分59秒
Bの場合、4月29日18時57分36秒から5月26日17時38分49秒
となる。
すると、3月は31日まであり、4月は30日までなので、Aが最もはなれたk−時刻となる。
◆千葉県 菜花子 さんからの解答

<求め方>
◆愛知県 Y.M.Ojisan さんからの解答
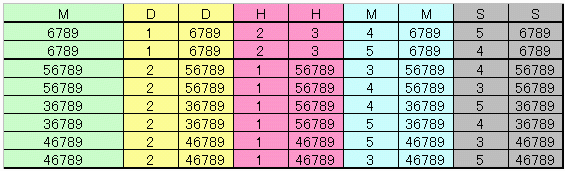
成立する組み合わせは上表の768通りである。
【問題1】
3月26日 17時48分:59秒
【問題2】
9月28日 17時56分43秒
【問題3】
9月28日 17時56分43秒 と 9月28日 17時56分34秒
∵同分台の秒数桁の交換は最少9秒、分を跨ぐと0がないので10秒以上になるから。
【問題4】
3月29日 18時57分46秒 と4月26日 17時38分59秒
差=27日22時間41分13秒
∵可能な限り桁上がりが多い月を跨ぐところを探索した。
◆岩手県 utu さんからの解答
「1月」などを「01月」というように置き換えれば、必ず10桁になる。
0を2個以上含むならば1〜9のいずれかは含まれないことになる。
したがって、0を含めた10種の数字が1回ずつ使われるとしてかまわない。
下の表のように桁を十月、一月、・・・、十秒、一秒と表すことにする。
まず、明らかに使わない部分を埋める。

まず、月について考えると、
01月のとき
十時の候補は2のみ。
20〜22は使えないので23時しかない。
すると、十日に入るものがなくなるのでアウト。
02月のとき
十時の候補は1のみ。
よって十日に入るのは3のみ。
ところが、30日、31日共に作れないのでアウト。
10月のとき
01月と同様の理由でアウト。
11月のとき
自動的にアウト。
12月のとき
十時の候補は0のみ。
よって十日に入るのは3のみ。
したがって、02月と同様にアウト。
この時点で、03月〜09月に限定された。
逆にいうと、他の場所に0は入らないことになる。
これで、30日は無くなった。
次に31日について考えると、十時の候補は2のみ。
しかし20〜23時はすべてアウト。
十日の候補から3が無くなったので、残りは1と2。
また、十時の候補も1と2なので、他の場所に1と2は入らない。
ここまでで消えた部分を埋めると下のようになる。
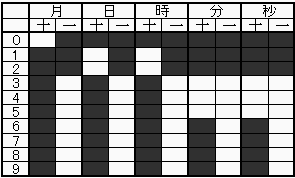
もう少し突っ込んで細かく見ると、
3月のときは当然23時は無し。
4月のときは3と5が、5月のときは3と4が、十分と十秒に入るので、23時は無し。
したがって3〜5月は、十時は1、十日は2と定まる。
6〜9月は23時の可能性もある。
このとき13〜15日は破綻が生じる。
13日のとき、十時の候補は2だが、20〜23時のいずれもアウト。
14、15日のとき、十一時の候補は23時のみ。
すると、十分十秒の候補が1つしか残らないのでアウト。
かなり候補が絞られてきたところで、解答。
【問題1】
03月26日17時48分59秒
左からなるべく小さい数字を配置
【問題2】
09月28日17時56分43秒
左からなるべく大きい数字を配置
【問題3】
09月28日17時56分34秒〜09月28日17時56分43秒 等 その差9秒
6〜9月の23時以外のとき、34秒、45秒を作ることが可能
これを取り替えれば、43秒、54秒となり、最近の時刻となる。
【問題4】
3月最終〜4月最初 すなわち
03月29日18時57分46秒〜04月26日17時38分59秒
年を越してもいいなら【問題2】の解〜【問題1】の解。
これはあまりにもなので、普通に考えると、5月以降は最終が29(28)日で、翌月の最初が16(17)日なので短い。
4月最終〜5月最初は、間に31日がないので短い。
◆茨城県 H2k さんからの解答
数字の数は9個。時分秒は各二桁。
よって月日の片方が2桁である必要がある。
【問題1】
可能な組み合わせとして、1月23日が初めの日。
456789で時分秒を作れないのでこれはダメ。
じゃあ、下から考えてみよう。
各数字を一回は使うんだから、秒を大きく、時を小さくするのが基本。
よってまず秒としてとりうる最大の値59秒。同様に48分。
この段階で残った数字は12367の5つ。
まず1月中にしたいので2367で日時を作りたい。無理。
次に2月。17時、36日。でダメ。
3月とすれば、3月26日17時48分59秒。
これが一番早いk-時刻。
【問題2】
まず12月を考えるが1,2が無いと時が作れない。
11月は1を2回使うのでダメ。10月は0が入るのでダメ。
ってことで9月で。
ここで作れる一番大きい日は28日。
残りから一番大きい時は17時。
次、一番大きい分は56分。で残り43秒。
よって9月28日17時56分43秒。
【問題3】
まず、近いものの作り方は分秒の数字を適当に入れ替えること。
問題2で使った9月28日17時56分43秒とそれを入れ替えた9月28日17時56分34秒を考えてみる。
この間9秒。
0が使えないから、分の数字を入れ替えると10秒以上の差が出る。
仮に整合性を無視したとしても59秒→12秒の13秒。
なので秒の数字を入れ替えるのが最短。
桁を入れ替えたとき最もその差が小さくなるのは10の位と1の位の数字が隣接しているとき。
つまり、12,23,34,45のどれか。
従って、9月28日17時56分43秒と9月28日17時56分34秒は最も近い2つの時刻のひとつである。
12秒、23秒、34秒、45秒のk-時刻は同様に最も近い時刻のk-時刻を持つハズ。
【問題4】
一年のうち最も早いのが3月26日。
最も遅いのが9月28日。
つまり9月28日→3月26日の間にはk-時刻が無い。
従って一番はなれたk-時刻は
3月26日17時48分59秒と9月28日17時56分43秒。
これは半年を越えていないので最長ではないかもしれない。
もし3月26日→9月28日の間にk-時刻が無ければそちらのほうが長くなるから。
そこで9月28日→3月26日が最長となるように3月26日→9月28日の間のk-時刻を上げておくことにする。
9月28日17時56分43秒から7と9を入れ替えても問題ないので7月28日19時56分43秒はk-時刻。
よって上に挙げた例が最長な2つのk-時刻である。
◆北海道 浜田 明巳 さんからの解答
エクセルのマクロで解きました.
【問題1】
3月26日17時48分59秒
【問題2】
9月28日17時56分43秒
【問題3】
答の間隔は9秒であり,次の48組ある.
6 27 18 39 45
6 27 18 39 54
6 27 18 59 34
6 27 18 59 43
6 27 19 38 45
6 27 19 38 54
6 27 19 58 34
6 27 19 58 43
6 28 17 39 45
6 28 17 39 54
6 28 17 59 34
6 28 17 59 43
6 28 19 37 45
6 28 19 37 54
6 28 19 57 34
6 28 19 57 43
6 29 17 38 45
6 29 17 38 54
6 29 17 58 34
6 29 17 58 43
6 29 18 37 45
6 29 18 37 54
6 29 18 57 34
6 29 18 57 43
7 26 18 39 45
7 26 18 39 54
7 26 18 59 34
7 26 18 59 43
7 26 19 38 45
7 26 19 38 54
7 26 19 58 34
7 26 19 58 43
7 28 16 39 45
7 28 16 39 54
7 28 16 59 34
7 28 16 59 43
7 28 19 36 45
7 28 19 36 54
7 28 19 56 34
7 28 19 56 43
7 29 16 38 45
7 29 16 38 54
7 29 16 58 34
7 29 16 58 43
7 29 18 36 45
7 29 18 36 54
7 29 18 56 34
7 29 18 56 43
8 26 17 39 45
8 26 17 39 54
8 26 17 59 34
8 26 17 59 43
8 26 19 37 45
8 26 19 37 54
8 26 19 57 34
8 26 19 57 43
8 27 16 39 45
8 27 16 39 54
8 27 16 59 34
8 27 16 59 43
8 27 19 36 45
8 27 19 36 54
8 27 19 56 34
8 27 19 56 43
8 29 16 37 45
8 29 16 37 54
8 29 16 57 34
8 29 16 57 43
8 29 17 36 45
8 29 17 36 54
8 29 17 56 34
8 29 17 56 43
9 26 17 38 45
9 26 17 38 54
9 26 17 58 34
9 26 17 58 43
9 26 18 37 45
9 26 18 37 54
9 26 18 57 34
9 26 18 57 43
9 27 16 38 45
9 27 16 38 54
9 27 16 58 34
9 27 16 58 43
9 27 18 36 45
9 27 18 36 54
9 27 18 56 34
9 27 18 56 43
9 28 16 37 45
9 28 16 37 54
9 28 16 57 34
9 28 16 57 43
9 28 17 36 45
9 28 17 36 54
9 28 17 56 34
9 28 17 56 43
つまり月,日,時,分までが同じで,秒の十の位と一の位の数が入れ替わったものが答の候補となる.
【問題4】
答の間隔は19日5時間1分23秒であり,次の1組ある.
5 29 18 47 36
6 17 23 48 59
つまり月が変わる時が間隔が最大になる候補になる.
マクロはこちらです。
◆兵庫県 sinapusu さんからの解答
マクロはこちらです。
上記コードの結果にオートフィルタを適用し整形。
一番近い日 時:秒:分
2003/6/27 19:38:45
2003/6/27 19:38:54 0:00:09
2003/6/27 19:58:34
2003/6/27 19:58:43 0:00:09
2003/6/28 17:39:45
2003/6/28 17:39:54 0:00:09
2003/6/28 17:59:34
2003/6/28 17:59:43 0:00:09
2003/6/29 18:37:45
2003/6/29 18:37:54 0:00:09
2003/6/29 18:57:34
2003/6/29 18:57:43 0:00:09
2003/7/26 19:38:45
2003/7/26 19:38:54 0:00:09
2003/7/26 19:58:34
2003/7/26 19:58:43 0:00:09
2003/7/29 16:38:45
2003/7/29 16:38:54 0:00:09
2003/7/29 16:58:34
2003/7/29 16:58:43 0:00:09
2003/8/26 17:39:45
2003/8/26 17:39:54 0:00:09
2003/8/26 17:59:34
2003/8/26 17:59:43 0:00:09
2003/8/29 17:36:45
2003/8/29 17:36:54 0:00:09
2003/8/29 17:56:34
2003/8/29 17:56:43 0:00:09
2003/9/26 18:37:45
2003/9/26 18:37:54 0:00:09
2003/9/26 18:57:34
2003/9/26 18:57:43 0:00:09
2003/9/27 16:38:45
2003/9/27 16:38:54 0:00:09
2003/9/27 16:58:34
2003/9/27 16:58:43 0:00:09
2003/9/28 17:36:45
2003/9/28 17:36:54 0:00:09
2003/9/28 17:56:34
2003/9/28 17:56:43 0:00:09
一番遠い日
2003/3/29 18:57:46
2003/4/26 17:38:59 670:41:13
◆ 問題へもどる
◆ 今週の問題へ