
◆千葉県 菜花子 さんからの解答
【問題1】 ー ー ー
| | |
ー ー
| | | |
ー
| | |
ー ー
考え方:
辺が4本のマッチ棒でできた正方形をSとする。
Sは9つ。
辺が8本のマッチ棒でできた正方形をMとする。
Mは4つ。
(図1の青、赤、紫、緑の線で囲った正方形)
辺が12本のマッチ棒でできた正方形をLとする。
Lは1つ。
(図1の黄の線で囲った正方形)
Mの4つの正方形の内側の、2つのSの正方形の境の1本を取ると、Sの正方形のう
ち8つが消滅。
このとき合わせて、Mの正方形は4つとも消滅。
Lの正方形から1本を取ると、Lの正方形が消滅。
残った1つのSの正方形から1本取ると、すべての正方形が消滅。
正方形がひとつもない状態にするには、少なくとも6本のマッチ棒を取り去ることが必要。
【問題2】は、上のことから、不可能です。
【おまけ】
正方形が一つもない状態にする方法
その1:マッチ棒を1本取って、長方形(1x2)にする。
または、正方形にならないようにする。
その2:マッチ棒を2本取って、長方形(1x3)にする。
または、L字型にする。
その3:マッチ棒を3本取って、長いL字型にする。
または、凸型にする。(図2)
これらの方法を組み合わせる。
(例として・・・図3)

◆東京都 fields さんからの解答
【問題1】 ー ー
| | |
ー ー ー
| | |
ー ー
| | |
ー ー
【問題2】
(マッチの長さは1とする。)
この図形には、1×1(小)、2×2(中)、3×3(大)の正方形
がそれぞれ、9,4,1の計14個含まれている。
マッチを5本取り除いただけでは、14個すべての正方形を消滅でき
ないことを以下証明する。
小の正方形のうち、図の中心に位置するものをとくに、核とよび、
それ以外の小の正方形だけを小、と以下よぶことにする。
よって、
この図形に含まれている小正方形は8つ、核は1つということになる。
マッチのうち、大正方形を構成するものを外、核を構成するものを
核、それ以外のものを内とよぶことにする。
以下それぞれのマッチ棒を取り除いたときに、最大どの正方形を
どれだけ消滅させることができるかを表にする。
| 大 | 中 | 小 | 核 | |
| 外 | 1 | 2 | 1 | 0 |
| 内 | 0 | 1 | 2 | 0 |
| 核 | 0 | 2 | 0 | 1 |
ここで、大、核の2正方形を消滅させるには、必ず、外1、核1
のマッチ棒を取り除く必要がある。
これによって、大、中、核
のすべての正方形が消滅しうる。
ただし、小正方形が7つ残る。
残り3本のマッチ棒をどのように選ぼうとも、最大で小正方形は
6つまでしか消滅させることができない。
よって、マッチを5本取り除いただけでは、14個すべての正方形を消滅でき
ないことがわかった。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
考え方は、問題2のAタイプを考えて、残された1×1の正方形2個を2本使って消去する ー ー ー
| | |
ー ー
| |
ー ー
| | |
ー ー ー
【問題2】
5回では不可能
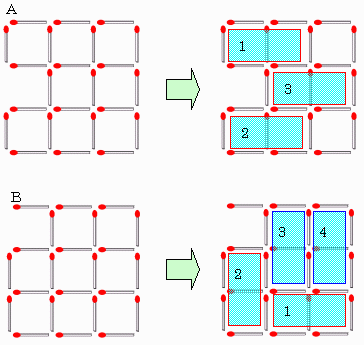
∵ 3×3の正方形を消すためには下図のA、B2通りの消し方がある。
このとき1×1の正方形が何れも8個残されるので、残りマッチ4本でこれらを全部消すにはそれらのマッチは両側には1×1の正方形がある。
つまり、内部にあるマッチでなければならない。
これはドミノを4個置けるかということと同じである。
また2×2の正方形も消えなければならないので、ドミノがぴったり平行に並んでも成立しません。
Aの場合は必然的に下図になり、ドミノを4個を置くことすらできず不可能です。
Bの場合は対称性を用いると必然的に下図1通りになり、
4個置くことはできますが平行なドミノ(3,4)があり不可能です。
【おまけ】
700とおり。 (対称形をまとめず)
PC解で考えます。
マッチ棒着目で、高々24C6=134596とおりのしらみつぶしであり、計算時間は僅かです。
実際には各マッチ棒(24要素)と正方形(14要素)の相関をビットマップで表し、
マッチ棒6要素のORが0x3FFFになるものの数が解答になります。
ソースを示します。
// 数学の部屋 第182回問題
// CopyRighted by Y.M.Ojisan
#include <stdio.h>
#include <stdlib.h>
int Matti[24];
// Mapping 3x3square#=[0]
// [1x1square#] [2x2square#]
// -01---02---03-
// 13[5]14[6]15[7]16 [1] [2]
// -04---05---06-
// 17[8]18[9]19[A]20 [3] [4]
// -07---08---09-
// 21[B]22[C]23[D]24
// -10---11---12-
int N=0;
void init()
{
int i,j,k,p;
for(i=0;i<24;i++) Matti[i]=0;
//3x3 square
p=1;
for(i=1;i<=3;i++)
Matti[i-1]|=p;
for(i=13;i<=21;i+=4)
Matti[i-1]|=p;
for(i=10;i<=12;i++)
Matti[i-1]|=p;
for(i=16;i<=24;i+=4)
Matti[i-1]|=p;
//2x2 square
for(j=0;j<=1;j++)for(k=0;k<=1;k++){
p<<=1;
for(i=1;i<=2;i++)
Matti[i-1+j+k*3]|=p;
for(i=13;i<=17;i+=4)
Matti[i-1+j+k*4]|=p;
for(i=7;i<=8;i++)
Matti[i-1+j+k*3]|=p;
for(i=15;i<=19;i+=4)
Matti[i-1+j+k*4]|=p;}
//1x1 square
for(j=0;j<=2;j++)for(k=0;k<=2;k++){
p<<=1;
Matti[1-1+j+k*3] |=p;
Matti[13-1+j+k*4]|=p;
Matti[4-1+j+k*3] |=p;
Matti[14-1+j+k*4]|=p;
}
}
int proc(int L,int i,int state)
{
int LEND=6; // L=5 → N=0
if(L==LEND)
{
if(state==0x3fff) N++;
}
else
{
int k;
for(k=i+1;k<=24-LEND+L;k++)
proc(L+1,k,state | Matti[k]);
}
return N;
}
void main()
{
int state=0;
init();
proc(0,-1,state);
printf("N=%d\n",N);
}
◆東京都 明 さんからの解答
【問題1】
ー ー ー | | ー ー | | | | ー | | | ー ー ー【問題2】
5本を取り除くのでは、少なくとも1つの正方形が残ります。
正方形は下記のC1〜C5,B1〜B4,D1〜D4,E の14個です。
ー ー ー |C1|B1|C2| ー ー ー |B4|C5|B2| ー ー ー |C4|B3|C3| ー ー ー ー ー | D1 | ー ー | | | | ー ー | D2 | ー ー ー ー | D3 | ー ー | | | | ー ー | D4 | ー ー ー ー ー | | | E | | | ー ー ーC1〜C5を構成するマッチ棒に共通するものはないため、5本を取り 除いてすべての正方形を壊すためにはC1〜C5を構成しているマッチ 棒を、それぞれから1本ずつ、計5本取り除く必要があります。
C1〜C5 の各1本のマッチ棒を取り除いた時、同時に壊すことのできる正方形を次の表にまとめます。
B1 B2 B3 B4 D1 D2 D3 D4 E
----------------------------------------------
C1 * *
* *
* *
-----------------------------------------------
C2 * *
* *
* *
-----------------------------------------------
C3 * *
* *
* *
-----------------------------------------------
C4 * *
* *
* *
------------------------------------------------
C5 * * *
* * *
* * *
* * *
-------------------------------------------------
C5 を構成するマッチ棒を取り除いて見ます。 B1 B2 B3 D1 D4 E
----------------------------------------------
C1 *
*
* *
-----------------------------------------------
C2 * *
*
*
-----------------------------------------------
C3 * *
*
*
-----------------------------------------------
C4 *
*
* *
------------------------------------------------どのマッチ棒を取り除いても同時には、たかだか2つの正方形しか壊せないため、6個の正方形を壊すためには、C1〜C4 の2つで、異なる4つの正方形を壊せる組み合わせがなくてはなりません。以上により5本を取り除くのでは、少なくとも1つの正方形が残ります。
【おまけ】
場合分けが大変なのでプログラムを組んでみました。
(仮称十進BASICをお借りしました。)
答えは700通りとなりました。
DECLARE EXTERNAL SUB zyun
DIM C(24) !マッチ棒の有無
DIM CHK(14) !正方形の有無
LET NS=0 !チェック数
LET NC=0 !適合数
REM マッチ棒の有無の初期設定
DATA 0,0,0,0,0,0,1,1,1,1
DATA 1,1,1,1,1,1,1,1,1,1
DATA 1,1,1,1
MAT READ C
DO
LET NS=NS+1
CALL check
CALL zyun(24,EX,C)
LOOP UNTIL EX=0
PRINT "チェック数 :";NS
PRINT "適合数 :";NC
STOP
SUB check
LET CHK(1)=C(21)*C(8)*C(9)*C(2)
LET CHK(2)=C(7)*C(22)*C(13)*C(10)
LET CHK(3)=C(11)*C(16)*C(23)*C(18)
LET CHK(4)=C(3)*C(12)*C(17)*C(24)
LET CHK(5)=C(1)*C(21)*C(8)*C(10)*C(11)*C(17)*C(24)*C(4)
LET CHK(6)=C(21)*C(5)*C(6)*C(22)*C(13)*C(11)*C(12)*C(2)
LET CHK(7)=C(9)*C(7)*C(22)*C(14)*C(15)*C(23)*C(18)*C(12)
LET CHK(8)=C(3)*C(9)*C(10)*C(16)*C(23)*C(19)*C(20)*C(24)
LET CHK(9)=C(1)*C(21)*C(5)*C(6)*C(22)*C(14)
LET CHK(9)=CHK(9)*C(15)*C(23)*C(19)*C(20)*C(24)*C(4)
LET CHK(10)=C(1)*C(2)*C(3)*C(4)
LET CHK(11)=C(5)*C(6)*C(7)*C(8)
LET CHK(12)=C(9)*C(10)*C(11)*C(12)
LET CHK(13)=C(13)*C(14)*C(15)*C(16)
LET CHK(14)=C(17)*C(18)*C(19)*C(20)
LET DET=0
FOR K=1 TO 14
LET DET=DET+CHK(K)
NEXT K
IF DET=0 THEN
LET NC=NC+1
!CALL output
END IF
END SUB
SUB output
PRINT "No";
PRINT USING "####":NC;
FOR K=1TO 24
IF C(K)=0 THEN PRINT USING "###":K;
NEXT K
PRINT
END SUB
END
!順列の変更
EXTERNAL SUB zyun(K,EX,N())
DECLARE EXTERNAL SUB seiretu
LET EX=0
LET J=1
DO
IF J>=K THEN EXIT DO
IF N(K-J)<N(K-J+1) THEN
CALL seiretu(J,K,N)
LET L=1
DO
IF N(K-J)>=N(K-J+L) THEN
LET L=L+1
ELSE
LET B=N(K-J)
LET N(K-J)=N(K-J+L)
LET N(K-J+L)=B
LET EX=1
EXIT DO
END IF
LOOP
EXIT DO
ELSE
LET J=J+1
END IF
LOOP
END SUB
!配列の整列
EXTERNAL SUB seiretu(J,K,N())
LET D=K-J+1
LET E=K
DO WHILE D<E
LET B=N(D)
LET N(D)=N(E)
LET N(E)=B
LET D=D+1
LET E=E-1
LOOP
END SUB
「CALL output」の前の「!」を削除すると取り除くマッチ棒の組み合わせが出力されます。
マッチ棒に付けた番号は下記のとおりです。
1 21 5
4 2 8 6
3 9 7
24 12 10 22
17 11 13
20 18 16 14
19 23 15
◆ 問題へもどる
◆ 今週の問題へ