【コメント】
東京都 K.N.I.F.E. さんからの情報によると、
2桁以上の数の先頭桁は0を含めず、それ以外は0を含む
(H, N, W, Sは1〜9、それ以外は0も含む)とすると、
Ans. 1) A=3, H=1, P=5, Y=7, N=4, E=0, W=6, R=9, S=2.
Ans. 2) A=3, H=1, P=5, Y=7, N=4, E=8, W=6, R=9, S=2.
Ans. 3) A=3, H=1, P=5, Y=7, N=4, E=0, W=9, R=6, S=2.
Ans. 4) A=3, H=1, P=5, Y=7, N=4, E=8, W=9, R=6, S=2.
Ans. 5) A=7, H=3, P=1, Y=5, N=8, E=2, W=0, R=9, S=4.
Ans. 6) A=7, H=3, P=1, Y=5, N=8, E=6, W=0, R=9, S=4.
Ans. 7) A=7, H=3, P=1, Y=5, N=8, E=2, W=9, R=0, S=4.
Ans. 8) A=7, H=3, P=1, Y=5, N=8, E=6, W=9, R=0, S=4.
の8種類になるそうです。
YEARに入る数値が未年の場合は、Ans. 5)のYEAR=5279だけだそうです。
また、SHEEPに入る数値が未年の場合は、残念ながらないそうです。
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】

【考え方】
各桁の桁上がりにかかわる条件から
(1) S=1+H
(2) A+Y+1=10+H
(3) P+N+1=10
(4) P+A+2=10 ((4)より)
(5) A+Y+W+R=P+20
(左辺は最大30でP≠0 また 最小10だが(3)と競合するので20に限る)
ほかに1〜9を使うので
(6) A+H+P+Y+N+E+W+R+S=45
以上から PとHをパラメータとして
(1) S=1+H
(2) Y=1+H+P
(3) N=9−P
(4) A=8−P
(5) W+R=11+P−H
(6) E=15−2H−P
である。
P,Hの探索は範囲は(4)(6)より
1≦P≦7、1≦H≦6、P≠Hおよび6≦2H+P≦14で
(2)よりH+P≦8であり20通りある。
あとはこれらをしらみつぶしした結果P,Hの組は1とおりのみOKであった。
W+Rの組み合わせで2通り。
◆大阪府 Non さんからの解答
一の位:
最小1+2+3+4=10、最大9+8+7+6=30だが1の位が0にはならないので、
繰り上がり1〜2
十の位:
P+A+繰り上がり=10
百の位:
P+N+1=10
千の位:
A+Y+1=10+H
(繰り上がりがなければ万の位でH=Sとなるので)
万の位:
H+1=S
一の位の繰り上がりを1とすると、A=Nとなってしまうので、一の位の繰り上がりは2。
このとき、P+A+2=10,P+N+1=10より、A+1=N
A+1=N,H+1=Sより、A≦8,H≦8でありAとHは1違いではない。
また、P+A=8より、Aは4や8ではない。
A+Y+1=10+Hより、Y=9+H-Aなので、考えられるH,A,Yの組み合わせは、
(H,A,Y)
=(1,3,7),(1,6,4),(1,7,3),(2,5,6),(2,6,5),(2,7,4),(3,5,7),(3,7,5),(4,6,7),(4,7,6)
A+1=N,H+1=S,P=8-Aより、(数字が重なるものを除くと)
(H,A,S,N,Y,P)
=(1,3,2,4,7,5), (2,7,3,8,4,1),(3,7,4,8,5,1),(4,7,5,8,6,1)
A+Y+W+R=P+20にそれぞれの値を代入すると順に、
3+7+W+R=25 W+R=15 (W,R)=(6,9),(9,6)
7+4+W+R=21 W+R=10 解なし
7+5+W+R=21 W+R=9 解なし
7+6+W+R=21 W+R=8 解なし
よって、
(H,A,S,N,Y,P,W,R,E)=(1,3,2,4,7,5,6,9,8),(1,3,2,4,7,5,9,6,8)
すなわち、解答は次の2通り。 3 3
13557 13557
486 489
+ 7839 + 7836
------ ------
21885 21885
◆千葉県 菜花子 さんからの解答
【問題1・2】
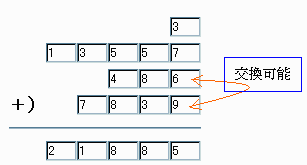
◆熊本県 hahi さんからの解答 3
13557
486
+ 7839
=21885
-------------
3
13557
489
+ 7836
=21885
プログラムを作成して解きました。
プログラムは、こちらです。
◆富山県 萩の葉 さんからの解答
【問題1】
3 3 13557 13557 489 486 + 7836 + 7839 ------------ ------------ 21885 21885【問題2】
1桁目について(A,Y,W,R)の
最小の組み合わせは(1,2,3,4)
A+Y+W+R=10
最大の組み合わせは(6,7,8,9)
A+Y+W+R=30
よって1桁目の繰り上がりは1または2である
1桁目の繰り上がりが1の場合
2桁目はP+E+A+1=10+E
3桁目はP+N+E+1=10+E
A=Nとなり不可
1桁目の繰り上がりが2の場合
1桁目はA+Y+W+R=20+P
2桁目はP+E+A+2=10+E
よって P=8−A
Y+W+R=28ー2A
3桁目はP+N+E+1=10+E
よって N=A+1
4桁目より H=A+Y−9・・・(a)
5桁目より S=H+1・・・(b)
A=1の時 P=7 N=2 Y+W+R=26
重複は許さないので(Y,W,R)の最大の組み合わせは
(9,8,6)
Y+W+R=23で不可
A=2の時 P=6 N=3 Y+W+R=24
重複は許さないので(Y,W,R)の組み合わせは
(9,8,7)のみである
(a)(b)よりY=9の時H=2 となり重複
Y=8の時H=1 S=2 となり重複
Y=6の時H=−1 となり不可
A=3の時 P=5 N=4 Y+W+R=22
重複は許さないので(Y,W,R)の組み合わせは
(9,7,6)のみである
(a)(b)よりY=9の時H=3 となり重複
Y=7の時H=1 S=2
残りのE=8となりW,Rは6,9いずれも可・・・成功!
Y=6の時H=0 となり不可
A=4の時 P=4 となり重複
A=5の時 P=3 N=6 Y+W+R=18
重複しない(Y,W,R)の組み合わせは
(9,8,1)(9,7,2)の2通りで、
残りの(E,H,S)の組み合わせは
(2,4,7)(1,4,8)となるがいずれも(b)を満たすことができないので不可
A=6の時 P=2 N=7 Y+W+R=16
重複しない(Y,W,R)の組み合わせは
(9,4,3)(8,5,3)の2通りで、
残りの(E,H,S)の組み合わせは
(1,5,8)(1,4,9)となるがいずれも(b)を満たすことができないので不可
A=7の時 P=1 N=8 Y+W+R=14
重複しない(Y,W,R)の組み合わせは
(9,3,2)(6,5,3)の2通り
(Y,W,R)=(9,3,2)の場合
(a)(b)よりY=9の時H=7 となり重複
Y=3の時H=1 S=2 となり重複
Y=2の時H=0 となり不可
(Y,W,R)=(6,5,3)の場合
残りの(E,H,S)の組み合わせは
(2,4,9)となり(b)を満たすことができないので不可
A=8の時 P=0となり不可
A=9の時 P=−1となり不可
◆東京都 明 さんからの解答
【問題2】
最初に各桁の繰り上がりを見積ります。
各桁のみに着目すると、
1桁目:10≦A+Y+W+R≦30かつP≠0 から 1または2
2桁目:P+E+A=E から 1
3桁目:P+N+E=E から 1
4桁目:A+Y=H から 0または1
さらに上の桁との関係を考慮すると
4桁目:1
1桁目:P+A+(1桁目繰り上がり)=10
P+N+1=10 から 2
と決定できます。
以上から下記のとおりとなります。
A+Y+W+R=P+20
P+A+2=10
P+N+1=10
A+Y+1=H+10
H+1=S
HとAを基本として書き換えると
S=H+1 (1)
Y=9+H-A (2)
P=8-A (3)
N=1+A (4)
W+R=19-H-A (5)
(2)から A>H
(3)から A≦7 よって H<7
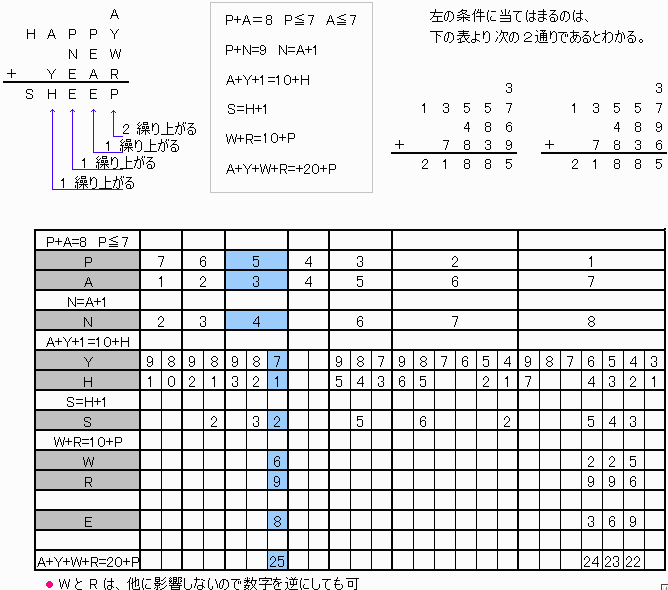
以上をベースに、下記表で数字が重ならないように順に選択し、数字が重なってしまう場合、候補から除外する。
H S A Y P N (W+R) W R E
6 7 -
5 6 7 -
4 5 6 7 2 -
4 5 7 6 1 8 (8) 2 -
3 -
3 4 5 7 -
3 4 6 -
3 4 7 5 1 8 (9) 2 -
6 -
2 3 4 7 -
2 3 5 6 -
2 3 6 5 -
2 3 7 4 1 8 (10) 5 -
6 -
9 -
1 2 3 7 5 4 (15) 6 9 8
8 -
9 6 8
1 2 4 6 -
1 2 5 -
1 2 6 4 -
1 2 7 3 -
結果、以下の2通りが適合します。A H P Y N E W R
3 1 5 7 4 8 6 9
3 1 5 7 4 8 9 6
◆ 問題へもどる
◆ 今週の問題へ