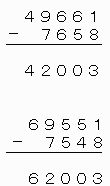
◆出題者のコメント
Non さんに座布団10枚です。
そのほかの皆様も解答ありがとうございました。
皆様の2003年は(=)良い(GOOD)年であることが約束されました。
おめでとうございます。
◆大阪府 Non さんからの解答
69551-7548=62003
ろく(69)なこ(5)となき、こ(5)の一(1)年、
な(7)んとかこ(5)とし(4)は、や(8)くはらい、
む(6)かうは新年二〇〇三(2003)。
49661-7658=42003
欲(49)張らず、無(6)欲、無(6)我にて、行(1)きましょう。
な(7)にも無(6)理せず、こ(5)まめにや(8)れば、
よ(4)りよい新年二〇〇三(2003)。
◆千葉県 菜花子 さんからの解答
G=2の場合、H−Yの組み合わせ
・・・9−7、8−6、7−5、6−4
D=3の場合、P−Rの組み合わせ
・・・9−6、8−5、7−4、1−8
O=0 の場合、
E=0、E−A=0、がともに成り立つためには、P−Rは繰下がりのある計算でなければならない。
したがって、P−R=1−8である。
H−Yの組み合わせは、9−7、7−5、6−4のどれかである。
A=6なら、E=7
A=5なら、E=6
A=4なら、E=5
すると、H−Y=6−4、H−Y=7−5、は成り立たない。
したがって、H−Y=9−7である。
また、A=5,4、E=6,5、であり、S=4,6である。
S=4,6 H=9 E=6,5 P=1 Y=7 A=5,4 R=8 G=2 O=0 D=3-------------------------------------------------------------------
問題の計算が成り立つのは、次の2通りである。
(2003年が入る場合)
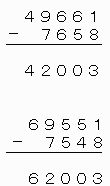
◆北海道 えんたー さんからの解答
まず、問題の「新年を祝うにふさわしい数字の並び」が「2003」であると仮定すると、これは「GOOD」のところにしか入らないことがわかります。
よって、(イ)G = 2, O = 0, D = 3
また、十の位に着目すると、E - A = 0 は成立しないので、一の位で繰り下がりが発生していることがわかります。
つまり、10 + P - R = 3 より R = P + 7
上の式より、(ロ)R = 1, P = 8
ところで、
十の位より E = A + 1(ハ)
千、万の位より H = Y + 2(二)
残りの数字 4,5,6,7,9
(二)を満たす H と Y について考えると、(ハ)より、1違いの数字のペアが必ず残らなければいけません。
よって、(ホ)H = 7, Y = 9 しか考えられません。
すると、(へ)A = 4, E = 5, S = 6 または (ト)A = 5, E = 6, S = 4
以上より、A = 4, D = 3, E = 5, G = 2, H = 9, O = 0, P = 1, R = 8, S = 6, Y = 7
または、 A = 5, D = 3, E = 6, G = 2, H = 9, O = 0, P = 1, R = 8, S = 4, Y = 7
よって、答えは 69551 - 7548 = 62003
または 49661 - 7658 = 42003
◆東京都 明 さんからの解答
S H E E P - Y E A R ------------ S G O O Dから以下が成り立つことがわかります。
O : 0または9
O : 0の時
H-Y=G
E-A=1
10+P-R=D
O : 9の時
H-Y=G+1
E-A=-1
P-R=D
「新年を祝うにふさわしい数字の並びが見えるものを」
ということで「GOOD」は「2003」ではと見当をつけました。
そうであれば、H,Y E,A P,Rの組み合わせはそれぞれ以下に制限されます。
(0,2,3は使用済み)
H Y E A P R
6 4 5 4 1 8
7 5 6 5
8 6 7 6
9 7 8 7
9 8
以上の組み合わせから数字が重ならない組み合わせを選ぶと以下の2通りとなります。H Y E A P R S 9 7 5 4 1 8 6 9 7 6 5 1 8 4以上から下記が答えとなります。
69551 - 7548 = 62003
49661 - 7658 = 42003
なお「(S)HEEP」が「2003」の場合は
E-A≠1からE-A=-1
よってA=1,O=9。
この場合、H(=2)-Y=G+1を成立させるためには、YもしくはGが0でなくてはならず、E(=0)とダブってしまい、式を成立させることができません。
◆広島県 清川 育男 さんからの解答
全解答はこちらです。
228 通り
◆ 問題へもどる
◆ 今週の問題へ