◆東京都 明 さんからの解答
【問題1】【問題2】
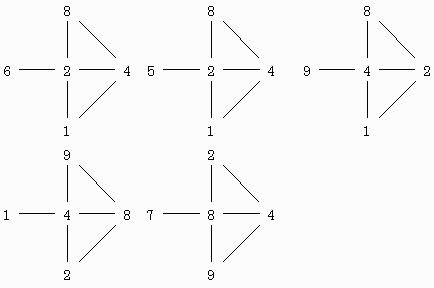
1〜9を9角形の頂点において、条件に合う2つの数を線で結び、できたグラフから条件に合うパターンを選びだしました。

【おまけ1】
面積:16
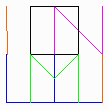
【おまけ2】
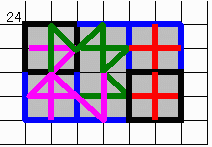
面積:24
◆東京都 mu-ya さんからの解答
【問題1】
4
|
2―1―9
|
3
【問題2】
11個(上下の入替で等しくなるパターンは一つとして数える)
2桁の7の倍数、13の倍数は以下のとおり
7:14,21,28,35,42,49,56,63,70,77,84,91,98
13:13,26,39,52,64,78,91
このうち、70,77は題意に合わない
また、91は重複、56と65もどちらかあればよいので、1つ削除する
残った16個の数字から、各桁の数字をカウントしていくと、
1:4個
2:5個
3:4個
4:4個
5:3個
6:3個
7:1個
8:4個
9:4個
計:32個となる。
この時点で5,6,7が中心には来ないことがわかる
後は以下のような表を作り、地道に数え上げていきました。
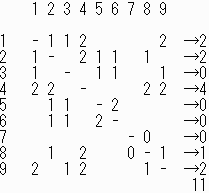
見方
表を横方向に見ていく
1とペアになる数字は2,3,4,9(21,13,14,91)
その中でペアになる数字の個数を数えると
2:1個→4(42)
3:1個→9(39)
4:2個→2(42),9(49)
9:2個→3(39),4(49)
ペアになる数字が2個あるときは、その数字を右に入れることが出来るので2通り
真ん中に2を入れた場合、右に来るのは4だけだが、5か6があまるので2通り
…といった感じです。
【おまけ1】
面積16
横線、縦線、斜めの線の数を比べると、
一目で縦線の数が多いことに気付く
縦線の数を数えると10本(長さにして20)ある
パターン1:1行10列に並べる
最小面積:18
パターン2:2行5列に並べる
最小面積:16
パターン3:3行4列に並べる
最小面積:18
パターン4:4行3列に並べる
最小面積:16
パターン5:5行2列に並べる
最小面積:16
このうちパターン4と5を最小面積で実際に並べるのは不可能
パターン2は、
上段:M、O、I
下段:L、N、L、I
を重ねて並べることで最小面積が可能となる
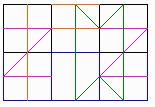
【おまけ2】
面積24
考え方は問題1とほぼ同じです。
◆愛知県 Y.M.Ojisan さんからの解答
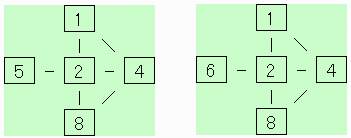
【問題1】
下図など
【問題2】
11組 ただし上下の対称性を区別しない。
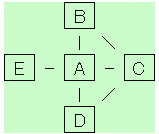
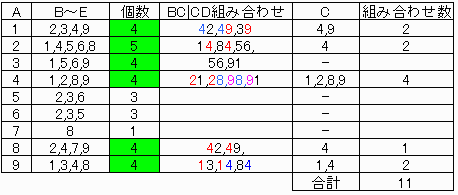
上図において[A]には条件を満たす組み合わせに4組以上かかわる数字を入れなければならない。
(下表で個数4または5のもの)
また[C]にはAと組になるものの数字間での条件を満たす組み合わせに、2組以上かかわる数字を入れなければならない。
以上を整理すると下表である。
なお、A=2の場合、Eには5または6が代入可能(問題1解答)なので、
組み合わせ数はCの可能性(=1)×2=2である。
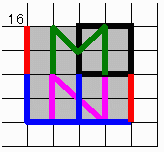
MILLION解答
【問題1】 16
【問題2】 24
◆ 問題へもどる
◆ 今週の問題へ