◆千葉県 なのはな子 さんからの解答
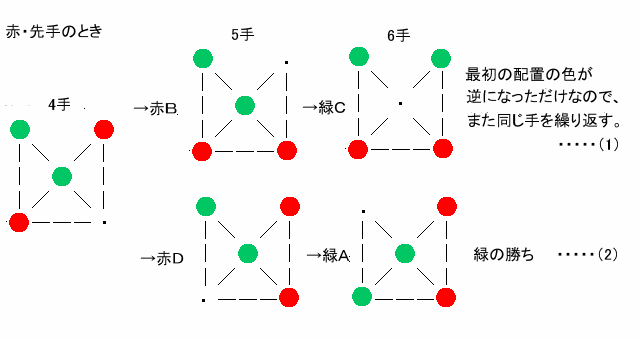
【問題1‐1】
緑が有利
【問題1‐2】
赤A→緑D→赤C→緑E→赤D (5手)
【問題1‐3】
どちらかが有利ということはない。
赤,緑とも先手後手にかかわらず、相手がミスしない限り勝てない。
双方が最善をつくすと同一手順を繰り返す。
緑が先手 先手の勝ち
[緑E→赤B→緑C→赤E→緑D→赤C→緑B]
緑が先手 後手の勝ち
[緑D→赤A→緑C→赤B→緑E→赤C→緑B→赤E→緑C→赤D→緑E→赤B]
赤が先手 後手の勝ち
[赤A→緑D→赤C→緑E→赤D→緑A]
赤が先手 先手の勝ち
[赤B→緑E→赤C→緑D→赤E→緑C→赤A]

◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】
緑が有利 下図の(12)→(8)
【問題1−2】
5手
下図の(1)→(10)→(11)→(3)→(4)→(12)
【問題1−3】
双方が最善を尽くすと千日手である。
∵ 局面は、左右対称なものを1個と数えると、全部で下図に示す16の局面がある。
ここで、手番の方は黒、相手は黄、空きを白とした。
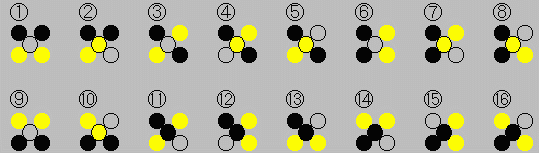
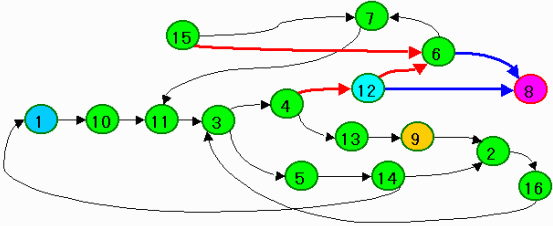
これらの遷移状態図を下図に示す。
初期状態は(1):赤先攻または(9):緑先攻であり、負けが決まるのは(8)である。
なお(12)は問題1−1の局面である。
赤矢印は必敗の手であり、青矢印は必勝の手である。
(1)から始まると、(4)で間違わない限り千日手である。
【問題2】
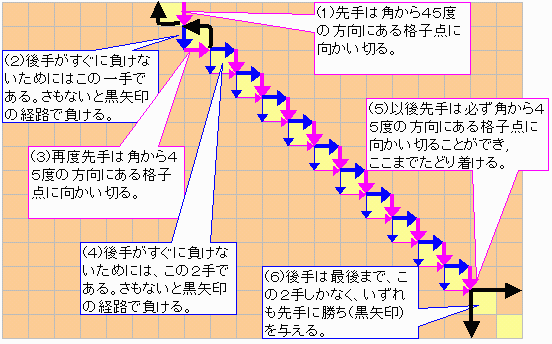
先手必勝である。
方眼の大きさをM×N M≦N とするとき、
一般に4≦M<Nにおいて下図の手順で先手必勝である。
(下図はM=14 N=20)
【考察】
4≦M<N以外の場合はどうであろうか。
●M=1の時は明らかに先手が必勝で、M=2の場合は後手が必勝である。下図
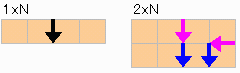
●M=3の場合下図のように 3×3を除き先手必勝である。
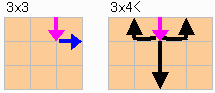
●4≦M=N の場合は単純ではない。
本題の手が使えるM=N=6の特殊な場合を除き、後手が必勝(黄色矢印)である。
N=M=4〜6の場合の手順は下記である。
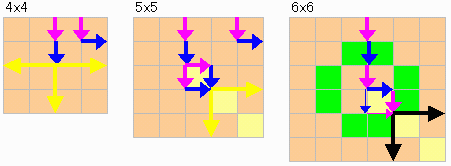
N=Mが7以上の場合は、次のように手をうつことにより、後手が必勝である。
まず、先手が一番端を切れば、即、後手は勝ちである(上図参照)。
先手が端から2番目以降に手を入れた場合、N>6なら図に示すような緑のセルの輪を作ることができる。
このセルの輪は傾きが45度で、最初の先手+後手の切り込みに2個連続して隣接したセルの部分を含む輪である。
下図例はN=M=10と8である。
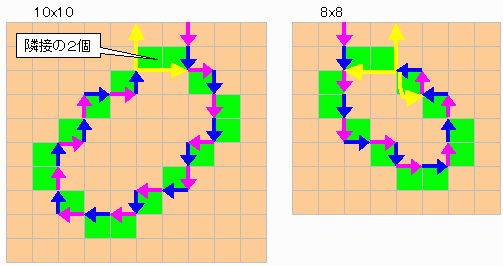
先手は、即負けないためにはこの緑のセルの輪から離れることができず、回転の方向も変えられない。
一方、後手はつねにこの輪を離れないように切ることができる。
従って、いずれ一周して元の位置に戻ってくるが、このとき、先手は端にも、すでに切り込んだ格子点にも、到達できない。
(黄色矢印)
なお、N=M=6が特殊なのは、このような最初の先手+後手の切り込みに2個連続して隣接した部分を作ることが必ずしもできないからだとも言える。
◆東京都 明 さんからの解答
【問題1−1】
緑 (緑A移動で詰み)
【問題1−2】
5手
(赤A→緑D→赤C→緑E→赤D)
【問題1−3】
互いに失策がなければ終了しない。
詰みの状態は(左右入れ替え型を同型として)下記の1つのみ。
○手番で
・ ○
×
× ○
(「・」が空の場所。「○」、「×」は赤または緑)
この一手前は、×手番で下記(イ)、(ロ)のいずれか。
(イ)× ○ (ロ)× ○
・ ×
× ○ ・ ○
(イ)のさらに一手前は○手番で下記(イ−1)、(イ−2)いずれか。
(イ−1)× ・ (イ−2)× ○
○ ○
× ○ × ・
(イ−1)の1手前は×手番だが、この状態へ移行できる場合がない。
したがって(イ−1)となる場合はない。
(イ−2)の場合互いに最善手を打つのであれば、右上○を下へ移動させれば×の詰みになる。
よって最善手を打つ限り、(イ)になる場合はない。
(ロ)の一手前は、○手番で下記の状態のみ。
× ○
×
○ ・
この場合、○は最善手を打つとすれば、次に詰まれないように右上の○を移動させるべきであり、したがって(ロ)の状態になることはない。
以上により、互いに失策がなければ、詰みの状態になることはないことはない。
【問題2】
1. 切り離し方に制限がない場合。
先手必勝
●方法
格子点の座標(x,y)を横方向をx、縦方向をyと定義し、
左上を(0,0)、右下を(45,30)とする。
(1)先手は(16,0)から(16,1)へカット。
(2)後手は(16,1)から(16,2)へカットの一手。
これ以外は次の先手が(x,0)へ切り離して先手勝ち。
(3)先手は(16,2)から(17,2)へカット。
(4)後手が(17,2)から(17,3)へカットした場合。
後手が(17,2)から(18,2)へカットした場合。
先手はいずれも(18,3)へカット。
後手が(17,2)から(17,1)へカットした場合。
先手は(17,1)から(16,1)へ切り離して先手勝ち。
(グラフ用紙の内部の1×1の正方形を切り離し。)
(5)以下、後手が負けないようにカットした場合、
先手は必ず(17+n,2+n)へカットをすることができる。
(6)以上を繰り返し、先手は(43,28)ヘカットを誘導することができる。
(7)次に後手がどのようにカットしても、先手は端への切り離し、もしくは内部の1×1の正方形の切り離しができる。
このルールではグラフ用紙がm×n(m>n≧4)では同じ様に隅へ追い込む戦略で先手必勝。
m=n≧7ではぐるぐる回しで後手必勝になるようです。
2.内部での切り離しを禁じ手とした場合。
(内部で切り離した方が負けの場合。)
先手必勝
●方法
座標のとり方は1.と同じとする。
(1)まず(2,2)−(43,28)を対角線とする長方形内の格子点の隣り合った2個をペアとした重複しない組を決めておく。
格子点は偶数個あり、すべての格子点を重複しないペアとして組み合わせを作ることができる。
(例)
・−・ ・−・ ・−・
・ ・ ・ ・ ・−・
| | | |
・ ・ ・ ・ ・−・
この範囲を以下説明のためF領域と呼ぶ。
(2)先手はどこでも、隅から2以上離れた位置からカットをする。
後手は負けないためにはF領域(の端)へカットをしなければならない。
(3)先手はカットの終点となったF領域の格子点とペアになった格子点へカットする。
(4)以下後手がカットした終点の格子点に対し、先手はF領域内のペアとなった格子点へ必ずカットができる。
(5)いずれ後手はF領域内ですでにカットされた格子点へカットを入れるか(禁じ手)、F領域外の格子点へカットをするしかなくなる。
F領域外がカットの終点になった場合は次のカット(先手の権利)で端まで切り離すことができる。(先手勝ち)
なお、2.のルールで勝負した場合、グラフ用紙が偶数×偶数の場合は格子点総数は奇数となり、後手が最初に切り込んだF領域の格子点を除いた偶数個の格子点でペアを作ることにより、同様の方法で後手が必勝になります。
◆ 問題へもどる
◆ 今週の問題へ