『今週の問題』第154回　解答

今回は３名の方から５段目に到達することが不可能な証明がきました。
論理の飛躍がある？ものもあるのですが、あえてそのまま掲載します。
この問題の考案者J. H. Conwayによる鮮やかな証明も掲載しておきます。

◆長崎県　嫉妬先生 さんからの解答

【問題１】

　＜最初の配置＞

＊，＊，＊，＊，蛙，
＊，＊，＊，＊，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，＊，＊，
＊，＊，＊，＊，＊，
＊，＊，＊，＊，＊，

(3,4)→(3,6)，(1,5)→(3,5)，(3,5)→(3,7)，(4,4)→(4,6)，
(5,4)→(5,6)，(5,6)→(3,6)，(3,6)→(3,8)，

　＜最初の配置＞

＊，＊，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，＊，蛙，
＊，＊，＊，＊，＊，

(3,4)→(3,6)，(1,5)→(3,5)，(3,5)→(3,7)，(4,4)→(4,6)，
(5,4)→(5,6)，(5,6)→(3,6)，(3,6)→(3,8)，(1,3)→(1,5)，
(2,3)→(2,5)，(1,5)→(3,5)，(3,2)→(3,4)，(7,5)→(5,5)，
(5,2)→(5,4)，(6,4)→(4,4)，(4,3)→(4,5)，(3,4)→(3,6)，
(5,5)→(3,5)，(3,5)→(3,7)，(3,7)→(3,9)，

不可能である。

＜説明＞

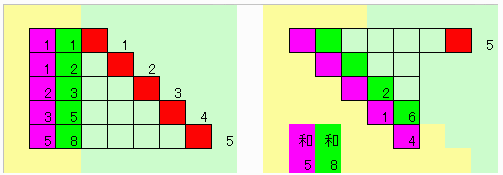
仕切り線より４段目にカエル最小・最小手順で移動させた後の形は下の図１のようになる。
ただし、これは、最初の配置で仕切り線より左側のマスすべてに（無限に）カエルを配置した場合である。

【図１】

蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，
蛙，蛙，＊，＊，＊，＊，＊，＊，＊，＊，
蛙，蛙，＊，＊，＊，＊，＊，＊，＊，＊，
蛙，＊，＊，＊，＊，＊，＊，＊，蛙，＊，
蛙，蛙，＊，＊，＊，＊，＊，＊，＊，＊，
蛙，＊，＊，＊，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，

【図２】

蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，
蛙，蛙，＊，○，○，＊，＊，＊，＊，＊，
蛙，蛙，＊，○，●，＊，＊，＊，＊，＊，
蛙，＊，＊，○，◎，＊，＊，△，蛙，＊，
蛙，蛙，＊，＊，○，＊，＊，＊，＊，＊，
蛙，＊，＊，＊，○，＊，＊，＊，＊，＊，
蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，

蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，     
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，
蛙，蛙，＊，＊，○，＊，＊，＊，＊，＊，
蛙，蛙，＊，＊，●，＊，＊，＊，＊，＊，
蛙，＊，＊，○，◎，＊，＊，△，蛙，＊，
蛙，蛙，＊，○，○，＊，＊，＊，＊，＊，
蛙，＊，＊，○，○，＊，＊，＊，＊，＊，
蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，＊，
蛙，蛙，蛙，蛙，蛙，＊，＊，＊，＊，＊，

例えば、まず◎印に移動するとすると、カエルまでの最小距離は３（真上のカエル）で、それを移動させてくるとしても、問題１より、少なくとも真上のカエル入れて上に２段、８個使うことになる。
（仕切り線があるので実際はもっと使う、または無理かも）

すると今度は●からの最小距離は４となり、移動のためには問題２より20匹のカエルを使うことになる。
その次は、最小距離は５以上となり（カエルを５段移動させたいのにその過程で５段以上移動させる必要があるのはおかしな話である）どんどん離れて行ってしまい永遠に無理である。

よってカエルが５段目に到達することは不可能である。

◆広島県　清川　育男 さんからの解答

【問題１】

＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，＊，蛙，
＊，＊，＊，＊，蛙，
＊，＊，＊，＊，＊，
＊，＊，＊，＊，＊，
＊，＊，＊，＊，＊，

(1,4)→(1,6)，(2,4)→(2,6)，(1,6)→(3,6)，(3,5)→(3,7)，
(5,5)→(3,5)，(3,4)→(3,6)，(3,6)→(3,8)，

20個で可能でした。

＊，＊，＊，＊，＊，
＊，＊，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，＊，蛙，

 (4,4)→(4,6)，(2,5)→(4,5)，(4,5)→(4,7)，(6,5)→(4,5)，
 (2,4)→(4,4)，(4,4)→(4,6)，(4,6)→(4,8)，(5,3)→(5,5)，
 (7,4)→(5,4)，(5,4)→(5,6)，(8,5)→(6,5)，(6,2)→(6,4)，
 (6,4)→(6,6)，(4,2)→(4,4)，(2,3)→(4,3)，(4,3)→(4,5)，
 (6,6)→(4,6)，(4,5)→(4,7)，(4,7)→(4,9)，

数列サイトに以下の数列がありました。

N=5は不可能。

Sequence: 1,2,4,8,20

Name: Number of initial pieces needed to reach level n in the Solitaire Army game.

References E. R. Berlekamp, J. H. Conway and R. K. Guy, Winning Ways, Academ Press, NY, 2 vols., 1982, see p. 715.

【おまけ】

　　　　　　　　○
　　　　　　　　□
　　　　　　　　□
　　　　　　　　□
　----------------------------
　　　　□□×あい××○○○　
　　　　　　□□う××○○○　
　　　　　□□□□□□○○○○
　　　　　　　□□　　○○○○
　　　　○○○○○○○　　
　　　　　　○○○○○
　　　　　○○○○○○
　　　　　　　○○
　　
　　　「　×あい××　
　　　　　　　う××　」

右側の○の一団で「う」が補填できる。
下側の○の一団で「あ」が補填できる。

【参考図】

○で×を補填する。

　１段　　　　　　　　　　　　　○
　　　　　　-----　-＞　　　　------
　　　　　　　○　　　　　　　　□
　　　　　　　○　　　　　　　　□



　２段　　　　　　　　　　　　　○
　　　　　　　○　　　　　　　　□
　　　　　　------　-＞　　---------　
　　　　　○○×　　　　　　□□□　　
　　　　　　　□　　　　　　　　□　　

　３段　　　　　　　　　　　　　　　○
　　　　　　　　○　　　　　　　　　□
　　　　　　　　□　　　　　　　　　□
　　　　　-----------　-＞　------------
　　　　　　□□×○○　　　　　□□□□□
　　　　　　○○×　　　　　　　□□□

　４段　　　　　　　　　　　　　　　○
　　　　　　　　○　　　　　　　　　□
　　　　　　　　□　　　　　　　　　□
　　　　　　　　□　　　　　　　　　□
　　　　-------------　-＞　-----------　　
　　　　○○×××□□　　　□□□□□□□
　　　　　　□□×○○　　　　　□□□□□
　　　　　○○○○○○　　　　□□□□□□
　　　　　　　○○　　　　　　　　□□

　５段
　　　　　　　　　　　○
　　　　　　　　　　　□
　　　　　　　　　　　□
　　　　　　　　　　　□
　　　----------------------------　-＞　？
　　　○○○○□□×××××○○○○
　　　○○○○○○×××□□○○○○
　　　○○○○○□□□□□□○○○○
　　　○○○○○○○□□○○○○○○
　　　○○○○○○○○○○○○○○○
　　　○○○○○○○○○○○○○○○
　　　○○○○○○○○○○○○○○○
　　　○○○○○○○○○○○○○○○
　　　○○○○○○○○○○○○○○○
　　　○○○○○○○○○○○○○○○

◆愛知県　Y.M.Ojisan さんからの解答

【問題１】　７手

＜初期＞

＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，蛙，蛙，
＊，＊，＊，＊，蛙，
＊，＊，＊，＊，蛙，

(3,4)→(3,6)，(2,4)→(2,6)，(1,4)→(1,6)，(5,5)→(3,5)，
(3,5)→(3,7)，(1,6)→(3,6)，(3,6)→(3,8)，

＜初期＞

＊，＊，＊，＊，蛙，
＊，＊，蛙，＊，蛙，
＊，＊，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，蛙，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，
＊，＊，蛙，蛙，蛙，

(5,4)→(5,6)，(7,5)→(5,5)，(5,5)→(5,7)，(6,3)→(6,5)，
(7,3)→(7,5)，(3,5)→(5,5)，(1,5)→(3,5)，(5,2)→(5,4)，
(5,4)→(5,6)，(5,6)→(5,8)，(4,3)→(4,5)，(2,3)→(4,3)，
(4,2)→(4,4)，(3,4)→(5,4)，(3,5)→(5,5)，(5,4)→(5,6)，
(7,5)→(5,5)，(5,5)→(5,7)，(5,7)→(5,9)

上図に示す様に、目標（赤）から境界（淡黄）までの
チェビシェフ距離＜:|x1-x2|+{y1-y2|＞が決まると必要なカエルの数が決まる（緑、紫）。

これは右図のように折れ曲がっていても合計は成立する。
因みに必要な数はフィボナッチ数列である。

１０列目は距離５である。
従って、少なくとも距離５（緑）に８匹、距離６（紫）に５匹が存在するか通過しなければならない。
つまり先ず、緑に７匹、外から飛んでこなければならない。

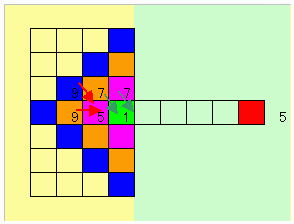
上図において、緑の７匹は紫から７匹、橙から７匹飛んでくる必要があり、都合紫は１２匹必要である。
然し紫は３箇所しか無く、９匹が外（橙と青）から飛んでくる必要がある。

一般に緑からのチェビシェフ距離をｎとするとき、
その位置に必要なカエルの数Ｆ_ｎは

Ｆ₀＝８
Ｆ₁＝５＋（Ｆ₀−１）＝１２
Ｆ₂＝（Ｆ₀−１）＋（Ｆ₁−３）＝１６
Ｆ₃＝（Ｆ₁−３）＋（Ｆ₂−５）＝２０

Ｆ_n+1
＝（Ｆ_n−（２ｎ＋１））＋（Ｆ_n-1−（２ｎ−１））
＝Ｆ_n＋Ｆ_n-1−４ｎ

これを計算すると　下表である。

n	0	1	2	3	4	5	6	7	8	9	10
Ｆn	8	12	16	20	24	28	32	36	40	44	48
Ｆn-(2n+1)	7	9	11	13	15	17	19	21	23	25	27

Ｆ_nの一般式は４ｎ＋８と予測されるが、代入すれば成立が確認される。

Ｆ_n＋Ｆ_n-1−４ｎ
＝４ｎ＋８＋４ｎ＋４−４ｎ
＝４ｎ＋１２
＝Ｆ_n+1

よって、外から飛んでくる必要のあるカエルの数
(Ｆ_n−（２ｎ＋１）)＝２ｎ＋７は単調に増加し、０にはならない。
即ちカエルの数は必ず不足する。
よって不可能である。

ちなみに　【問題２】のときは

Ｆ₀＝５
Ｆ₁＝３＋（Ｆ₀−１）＝７

n	0	1	2	3	4
Ｆn	5	7	8	7	3
Ｆn-(2n+1)	4	4	3	0	-6

より　ｎ＝４から解決の可能性が出てくる。
実際はｎ＝５が最小みたいである。

◆この問題を考案したJ. H. Conwayによる証明

ｒ²＋ｒ¹＝ｒ⁰（＝１）を満たす正数ｒを用いて
縦・横に無限に広がったマス目に図のように数値を割り当てる。
青色のｒ⁰が書かれているのが目標とするマス目である。

・・・

１

２

３

４

５

６

７

８

９

10

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

１

・・・

ｒ13

ｒ12

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

２

・・・

ｒ12

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

３

・・・

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

ｒ2

４

・・・

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

ｒ2

ｒ1

５

・・・

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

ｒ2

ｒ1

ｒ0

６

・・・

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

ｒ2

ｒ1

７

・・・

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

ｒ2

８

・・・

ｒ12

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

ｒ3

９

・・・

ｒ13

ｒ12

ｒ11

ｒ10

ｒ9

ｒ8

ｒ7

ｒ6

ｒ5

ｒ4

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

・ ・

ｒ^k＋ｒ^k-1＝ｒ^k-2(ｒ²＋ｒ¹)＝ｒ^k-2
が成立するので、蛙が左から右へと飛び移っても、蛙のいるマス目に書かれている数値の和は変わらない。
逆に蛙が右から左へと飛び移ると、蛙のいるマス目に書かれている数値の和は必ず小さくなる。

したがって「目標のマス目に書かれた数値ｒ⁰＝１」と「最初に蛙のいたマス目に書かれた全ての数値の和Ｓ」を比べて
Ｓ＜ｒ⁰＝１であれば、５段目に飛び移ることは不可能ということがわかる。

Ｓが最大になるのは、全てのマス目に蛙がいる場合であるから、その場合のＳを求める。

目標のマス目のある５行目（黄色のマス目）に書かれている数値の和は

　ｒ⁵＋ｒ⁶＋ｒ⁷＋ｒ⁸・・・

＝ｒ5（１＋ｒ1＋ｒ2＋ｒ3・・・）

＝

ｒ5 １−ｒ

＝

ｒ5 ｒ2

＝ｒ3

同様に４行目と６行目（緑色のマス目）に書かれている数値の和はそれぞれ

ｒ6＋ｒ7＋ｒ8＋ｒ9・・・＝

ｒ6 ｒ2

＝ｒ4

さらにその外側の３行目と７行目に書かれている数値の和はそれぞれｒ⁵

したがって

Ｓ＝ｒ3＋２(ｒ4＋ｒ5＋ｒ6＋・・・)

＝(ｒ3＋ｒ4＋ｒ5＋ｒ6＋・・・)＋(ｒ4＋ｒ5＋ｒ6＋・・・)

＝

ｒ3 １−ｒ

＋

ｒ4 １−ｒ

＝

ｒ3 ｒ2

＋

ｒ4 ｒ2

＝ｒ＋ｒ2

＝１

以上により無限にある全てのマス目に蛙がいる場合に、ようやくそこに書かれている数値の和が１に等しいことがわかる。

したがって５段目に飛び移ることは不可能である。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる