◆広島県 清川 育男 さんからの解答
【問題1−1】猪,兎,牛
兎,牛,猪
牛,猪,兎
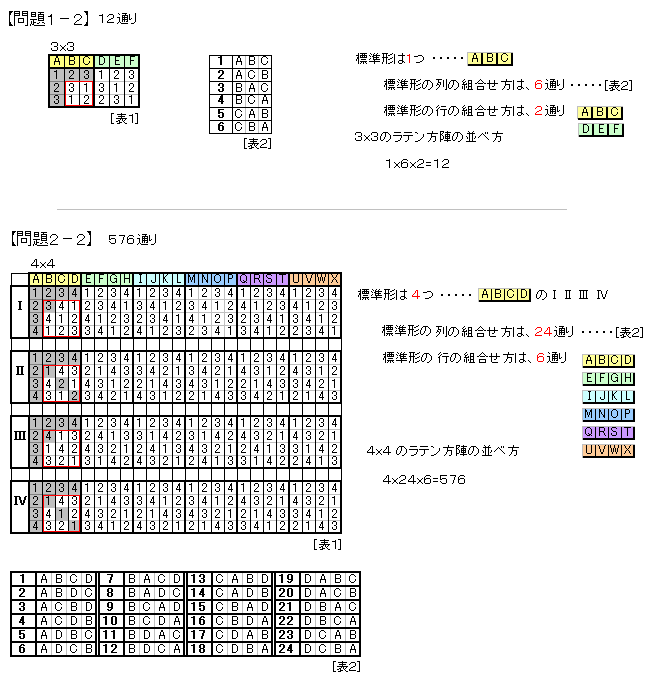
【問題1−2】
12通り。
【問題2−1】猪,兎,牛,猫
兎,牛,猫,猪
牛,猫,猪,兎
猫,猪,兎,牛
【問題2−2】
576通り。
【おまけ】
108776032459082956800通り。
1,2,12,576,161280,812851200,
61479419904000,108776032459082956800,
5524751496156892842531225600,
9982437658213039871725064756920320000
◆千葉県 なのはな子 さんからの解答
【問題1−1】牛,猪,兎
兎,牛,猪
猪,兎,牛
【問題2−1】猫,牛,猪,兎
猪,兎,猫,牛
牛,猫,兎,猪
兎,猪,牛,猫
【問題1−2】と【問題2−2】

ラテン方陣って初めて知りました。おもしろいものですね。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】猪,兎,牛
牛,猪,兎
兎,牛,猪
【問題1−2】
12とおり
∵ ラテン方陣成立状態に対して3匹の任意の置換はラテン方陣である。
よって、第一行を固定し結果を3!倍=6倍してよい。
6個の置換のうち、恒等置換1個と互換3個を除くと2個の巡環置換が残り、2行目は各2通り可能である。
3行目は選択の余地なしである。
よって全部で6×2=12とおりである。
【問題2−1】猪,兎,牛,猫
猫,猪,兎,牛
牛,猫,猪,兎
兎,牛,猫,猪
【問題2−2】
576とおり
∵ ラテン方陣成立状態に対して4匹の任意の置換はラテン方陣である。
よって、第一行を固定(猪,兎,牛,猫)し
結果を4!倍=24倍してよい。
第2行において(猪)の置き先は2,3,4列目の3通りあるが対称であるから、2列目に固定して結果を3倍してよい。
兎の置き先は(1)1列目 (2)3または4列目の2タイプである。
(1)の場合、2行目は(兎、猪、猫、牛)に限られる。
よって3行目は、1、2列目が猫と牛、3、4列目が兎と猪が自由にえらべて都合4通りである。
(2)の場合2行目は3列4列の対称性から(猫、猪、兎、牛)に限って2倍すればよい。
この時3行目は(牛、猫、猪、兎)(兎、牛、猫、猪、)の2とおりだけ可能である。
4行目は選択の余地なしである。
よって 24×3×(4+2×2)=576
【おまけ1】
【準備1】
n個のものの置換の数T(n)は T(n)=n!
∵周知
【準備2】
n個のものの置換で移動しないものが無いものの数D(n)は次の漸化式を満たす。
なお、D(1)=0 であり、D(0)=1 とする。
D(n)=T(n)-nC1*D(n-1)-nC2*D(n-2) ...- nCn-1 *D(1)-D(0)
∵上式は単純に全置換から、1個だけ一致するもの、2個だけ一致するもの、...、全部一致するもの(1個)を引いているだけである。
【準備3】
n個のものの置換で特定の1個を除き移動しないものが無いものの数D(n,1)は次の漸化式を満たす。
なお、D(1,1)=1 である。
D(n,1)=D(n-1)+(n-1)*D(n-1,1)=D(n+1)/n=D(n-1)+D(n)
∵上式は特定の1個が移動しない場合と、残りn-1個所に移動した場合の数の和である。
【準備4】
n個のものの置換で特定の2個を除き移動しないものが無いものの数D(n,2)は次の漸化式を満たす。
なお、D(1,2)=0 とする。
D(n,2)=D(n,1) + D(n-1,1)
∵上式は特定の2個のうち1個を通常状態とした場合の数と、その1個を移動しなかった場合の数の和である。
なお一般にはD(n,m)=D(n,m-1)+D(n-1,m-1)
以上の計算結果を下表に示す。
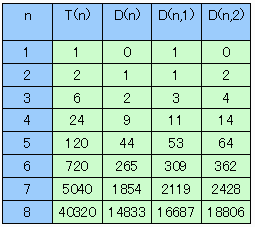
【上限】
行の置換、列の置換はラテン方陣の状態を崩さないので、
8×8セルの一行目と一列目の配置を固定(黄色セル)して
8!×7!倍すればよい。
2列目(緑セル)は1列目に対して、全て移動する置換で1つが固定されている置換の数の可能性がある。
即ち、D(7,1)=D(8)/7=2119個である。
2〜8行目は1行目に対して、全て移動する置換の可能性があるが、1列目と2列目が固定されているので、固定されたものの状態により
D(6)かD(6,1)かD(6,2)とおりの可能性がある。
これらの最大値は362である。
6行目に関しては特定の1種に関してみると3箇所が残されているだけなので
最大の可能性は3*3*3*3*2=162(<362)とおりである。
同様に7行目は2の5乗=32とおり,8行目は1とおりが最大である。
よって、上限値として
8!*7!*2119*3624*2*34*25≒3.84×1025
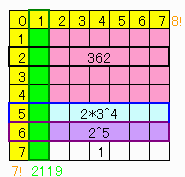
【下限】
行の置換、列の置換はラテン方陣の状態を崩さないので、
8×8セルの一行目と一列目の配置を固定(黄色セル)して
8!×7!倍すればよいのは上限と同じ。
セルを下図のように4×4のラテン方陣4個に分けて、個々に数えると
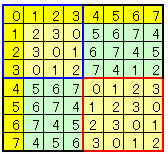
赤枠は問題2より576通り。
黒枠は1列制限されているので
576/4!=24とおり。
青枠は1行1列制限されているので
576/4!/3!=4とおり。
4×4への分け方は 8C4/2=35とおりである。
よって、下限値として
8!*7!*35*576*242*4≒9.44×1015
【感想】
おまけは多様なこたえが出てきて面白い問題になるでしょう。
余裕があればもう少し狭めたいところです。
正解は多分1020あたりでしょう。
PCで計算してみました。
108,776,032,459,082,956,800
◆ 問題へもどる
◆ 今週の問題へ