『今週の問題』第151回　解答

◆千葉県　なのはな子 さんからの解答

【問題１】

(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,1)→(4,3)→(3,5)→(4,7)→
(2,8)→(1,6)→(2,4)→(1,2)→(3,3)→
(4,5)→(3,7)→(1,8)→(2,6)→(1,4)→
(2,2)→(4,1)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,5)→(1,4)→(2,2)→(4,1)→
(3,3)→(4,5)→(3,7)→(1,8)→(2,6)→
(4,7)→(2,8)→(1,6)→(2,4)→(1,2)→
(3,1)→(4,3)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,1)→(1,2)→(2,4)→(4,3)→
(3,5)→(4,7)→(2,8)→(1,6)→(3,7)→
(1,8)→(2,6)→(1,4)→(2,2)→(4,1)→
(3,3)→(4,5)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,5)→(1,4)→(2,2)→(4,1)→
(3,3)→(1,2)→(3,1)→(4,3)→(2,4)→
(4,5)→(2,6)→(1,8)→(3,7)→(1,6)→
(2,8)→(4,7)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,1)→(4,3)→(3,5)→(4,7)→
(2,8)→(1,6)→(3,7)→(1,8)→(2,6)→
(1,4)→(2,2)→(4,1)→(3,3)→(4,5)→
(2,4)→(1,2)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,1)→(1,2)→(2,4)→(4,3)→
(3,5)→(4,7)→(2,8)→(1,6)→(3,7)→
(1,8)→(2,6)→(4,5)→(3,3)→(4,1)→
(2,2)→(1,4)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,1)→(4,3)→(3,5)→(1,4)→
(2,2)→(4,1)→(3,3)→(1,2)→(2,4)→
(4,5)→(3,7)→(1,8)→(2,6)→(4,7)→
(2,8)→(1,6)→
-----------------------------------
(1,1)→(3,2)→(4,4)→(3,6)→(4,8)→
(2,7)→(4,6)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(4,2)→(3,4)→(1,5)→
(2,3)→(3,5)→(1,6)→(2,8)→(4,7)→
(2,6)→(1,4)→(2,2)→(4,1)→(3,3)→
(1,2)→(3,1)→(4,3)→(2,4)→(4,5)→
(3,7)→(1,8)→
-----------------------------------
-----------------------------------
(1,2)→(3,1)→(4,3)→(2,4)→(1,6)→
(2,8)→(4,7)→(2,6)→(1,8)→(3,7)→
(4,5)→(3,3)→(4,1)→(2,2)→(1,4)→
(3,5)→(2,7)→(4,8)→(3,6)→(4,4)→
(3,2)→(1,1)→(2,3)→(1,5)→(3,4)→
(4,6)→(3,8)→(1,7)→(2,5)→(1,3)→
(2,1)→(4,2)→
-----------------------------------
(1,3)→(2,1)→(4,2)→(3,4)→(4,6)→
(3,8)→(1,7)→(3,6)→(4,8)→(2,7)→
(1,5)→(2,3)→(1,1)→(3,2)→(4,4)→
(2,5)→(3,7)→(1,8)→(2,6)→(4,5)→
(3,3)→(4,1)→(2,2)→(1,4)→(3,5)→
(4,3)→(3,1)→(1,2)→(2,4)→(1,6)→
(2,8)→(4,7)→
-----------------------------------
(1,4)→(2,2)→(4,1)→(3,3)→(1,2)→
(3,1)→(4,3)→(2,4)→(4,5)→(3,7)→
(1,8)→(2,6)→(4,7)→(2,8)→(1,6)→
(3,5)→(2,7)→(4,8)→(3,6)→(4,4)→
(3,2)→(1,1)→(2,3)→(1,5)→(3,4)→
(4,6)→(3,8)→(1,7)→(2,5)→(1,3)→
(2,1)→(4,2)→
-----------------------------------
(1,5)→(2,7)→(4,8)→(3,6)→(4,4)→
(3,2)→(1,1)→(2,3)→(4,2)→(2,1)→
(1,3)→(3,4)→(4,6)→(3,8)→(1,7)→
(2,5)→(3,7)→(1,8)→(2,6)→(4,5)→
(3,3)→(4,1)→(2,2)→(1,4)→(3,5)→
(4,3)→(3,1)→(1,2)→(2,4)→(1,6)→
(2,8)→(4,7)→
-----------------------------------
(1,6)→(2,8)→(4,7)→(2,6)→(1,8)→
(3,7)→(4,5)→(2,4)→(1,2)→(3,1)→
(4,3)→(2,2)→(4,1)→(3,3)→(1,4)→
(3,5)→(2,7)→(4,8)→(3,6)→(4,4)→
(3,2)→(1,1)→(2,3)→(1,5)→(3,4)→
(4,6)→(3,8)→(1,7)→(2,5)→(1,3)→
(2,1)→(4,2)→
-----------------------------------
(1,7)→(3,8)→(4,6)→(2,5)→(1,3)→
(2,1)→(4,2)→(3,4)→(1,5)→(2,7)→
(4,8)→(3,6)→(4,4)→(3,2)→(1,1)→
(2,3)→(3,1)→(4,3)→(3,5)→(1,4)→
(2,2)→(4,1)→(3,3)→(4,5)→(3,7)→
(1,8)→(2,6)→(4,7)→(2,8)→(1,6)→
(2,4)→(1,2)→
-----------------------------------
(1,8)→(2,6)→(1,4)→(2,2)→(4,1)→
(3,3)→(4,5)→(3,7)→(1,6)→(2,8)→
(4,7)→(3,5)→(4,3)→(3,1)→(1,2)→
(2,4)→(3,2)→(1,1)→(2,3)→(4,4)→
(3,6)→(4,8)→(2,7)→(1,5)→(3,4)→
(4,6)→(3,8)→(1,7)→(2,5)→(1,3)→
(2,1)→(4,2)→
-----------------------------------

◆東京都　高橋　英文 さんからの解答

【問題１】

(1,1)→(2,3)→(1,5)→(2,7)→(4,8)→
(3,6)→(1,7)→(2,5)→(4,4)→(3,2)→
(1,3)→(2,1)→(4,2)→(3,4)→(4,6)→
(3,8)→(2,6)→(1,4)→(2,2)→(4,1)→
(3,3)→(1,2)→(3,1)→(4,3)→(3,5)→
(4,7)→(2,8)→(1,6)→(2,4)→(4,5)→
(3,7)→(1,8)→

32コのマス目のうち１列目と４列目の集合をＡ，２列目と３列目の集合をＢとする

すなわち、

Ａ＝{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8)}
Ｂ＝{(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(3,7),(3,8)}

(*)
Aの任意の元aに対して、aから移動可能なAの元は存在しない。

ここで、得られた履歴を以下の例のように書く

(1,1)→(2,3)→(1,5)→(2,7)→(4,8)→
(3,6)→(1,7)→(2,5)→(4,4)→(3,2)→
(1,3)→(2,1)→(4,2)→(3,4)→(4,6)→
(3,8)→(2,6)→(1,4)→(2,2)→(4,1)→
(3,3)→(1,2)→(3,1)→(4,3)→(3,5)→
(4,7)→(2,8)→(1,6)→(2,4)→(4,5)→
(3,7)→(1,8)→

ABABABABABABABABBABABABABABABABABA

(**)
(1,1)から出発して全てのマスを通る履歴で考えられるのは、以下の通り

ABABABABABABABABABABABABABABABABAB---(1)(ABが互いに交互)
ABABABABABABABABABABABABABABABABBA---(2)(BBが最後から二つ目)
ABABABABABABABABABABABABABABABBABA---(3)(BBが最後から三つ目)
.
.
ABBABABABABABABABABABABABABABABABA---(14)(BBが最初から二つ目)

ところが(1)のケースはありえない

つまり、

(***)
(1,1)から出発して全てのマスを通る履歴で考えられるのは、以下の通り

ABABABABABABABABABABABABABABABABBA---(2)
ABABABABABABABABABABABABABABABBABA---(3)
.
.
ABBABABABABABABABABABABABABABABABA---(14)

何故ならば、 (1)の場合は、16手までで以下のようになる(証明略）

○×○×○×○×
○×○×○×○×
×○×○×○×○
×○×○×○×○

(1)の場合は、16手目はＢの元で、17手目がＡの元である。
これは不可能である。

(***)から以下のことがわかった。

(****)
(1,1)から出発して32個のマス全てを通る場合の終点は1列目または4列目である。

もしも、ナイトが一つのマス目から出発して、他の全てのマス目を１回ずつ通過して最後に元のマス目にもどるような手順があるとすると

(1,1)から出発して二手目で(2,3)を通過すると終点は(3,2)
(1,1)から出発して二手目で(3,2)を通過すると終点は(2,3)である。

これは(****)に反する。

よって【問題２】の答えは存在しない。

◆愛知県　Y.M.Ojisan さんからの解答

【問題１】

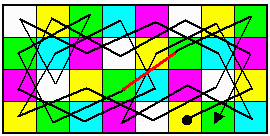
【問題２】　不可能

（１）上下の移動だけ考える。
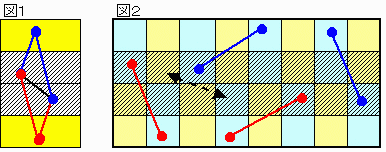
図１に示す様に、最上下の各列上には連続して留まれず、最上下列のグループ要素（黄色）の間には、必ず少なくとも１央２列のグループ（ハッチング）の要素が入る。

最上下列のグループは１６個あるのでその間は１５個あり、一方中央２列グループは１６個であるから、そのパターンは図３に示す三種である。

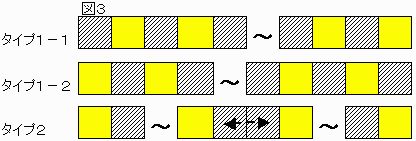
type1-1とtype1-2は順番を逆転すれば同じであり、まとめて考えればよい。
type２は問題１の解答のタイプであり、これは存在している。
type２は最初と最後が黄色であるから、ループを作ることは無い。

　よって、ループを作るなら少なくともtype1が存在しなければならない。
ところがタイプ１には中央２列内部間の移動はないので、結局図１の黒線の移動はできず、赤と青で示される移動のみである。
これを元の盤に戻すと図２であり、図２において色分けした薄黄のグループと空色のグループ間での移動ができない。
すなわち、黒線の移動なしでは、全セルを通過することはできない。

よって、type１の解は存在せず、ループ経路は存在しない｡

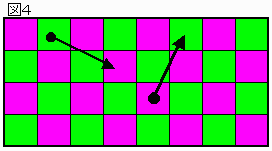
（２）因みに全部で３１回＝奇数回移動するので、図４に示すように赤紫セルから出発すれば緑セル、緑セルから出発すれば赤紫セルで終了する。

【おまけ１】

出発点として選ぶことができないマス目はある。
問題２の解答から判る様に、中央の２列は終点になり得ない。
これは逆経路を考えれば即ち、図２ハッチング部の中央の横２列は出発点にはなりえない。

【おまけ２】

最も単純にPCで探索した結果です。

　（１，１）から７６３０通り
　（１，２）から２７４０通り
　（１，３）から２０６６通り
　（１，４）から３１０８通り

合計は　(7630+2740+2066+3108)*4 = ６２１７６通り

短いプログラムなので添付しておきます。

ym_nigthtour151.c

【問題２別解】

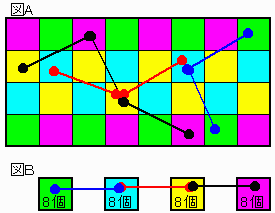
　盤面を図Ａのように色分けした４群８個づつに分ける。
すると、桂馬飛による４群間の移動は図Ｂに示される３経路（赤、黒、青）に限られる。
ループ経路であるためには各群は８回ずつ通過しなければならず、緑群と赤紫群を通過するためには少なくとも青と黒経路を１６回ずつ通過しなければならない。
更に赤経路を最低１往復しなければ全体を通過できないので経路通過数は合計３４以上必用である。
一方、ループ時の全通過経路数は３２であるので矛盾する。
すなわち、ループ経路は存在しない。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる