◆島根県の中学校3年生 成功 さんからの解答
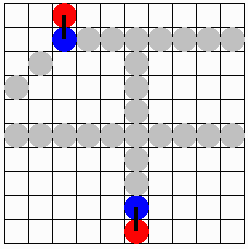
【問題1】
(1,3)→(2,3)→(2,6)→(3,6)→(3,2)→
(6,2)→(6,7)→(2,7)→(2,10)→(6,10)→
(6,1)→(4,1)→(4,6)→(10,6)
14回
【問題2】
(9,2)→(9,8)→(10,8)→(10,4)→(2,4)→
(2,3)→(7,3)→(7,10)→(8,10)→(8,2)→
(3,2)→(3,5)→(6,5)→(6,10)→(5,10)→
(5,1)→(4,1)
17回でできました。
【問題3】
(10,1)→(1,1)→(1,2)→(10,2)→(10,8)→
(1,8)→(1,5)→(6,5)→(6,10)
9回
【青木コメント】
正解第一号です。
◆広島県 清川 育男 さんからの解答
【問題1】
後戻り禁止のルールが局面を狭くしているようです。
14 手
1 ( 1, 3)→( 2, 3)→( 2, 5)→( 6, 5)→( 6, 2)→ ( 3, 2)→( 3, 6)→( 2, 6)→( 2,10)→( 6,10)→ ( 6, 1)→( 4, 1)→( 4, 6)→(10, 6)→ 2 ( 1, 3)→( 2, 3)→( 2, 5)→( 6, 5)→( 6, 2)→ ( 3, 2)→( 3, 6)→( 4, 6)→( 4, 1)→( 6, 1)→ ( 6,10)→( 2,10)→( 2, 6)→(10, 6)→ 3 ( 1, 3)→( 2, 3)→( 2, 6)→( 3, 6)→( 3, 2)→ ( 6, 2)→( 6, 7)→( 2, 7)→( 2,10)→( 6,10)→ ( 6, 1)→( 4, 1)→( 4, 6)→(10, 6)→最短手数は14手のようです。
3通り。
【問題2】
17 手
1 ( 9, 2)→( 9, 8)→( 7, 8)→( 7, 3)→( 2, 3)→ ( 2, 4)→(10, 4)→(10, 8)→( 6, 8)→( 6, 5)→ ( 3, 5)→( 3, 2)→( 8, 2)→( 8,10)→( 5,10)→ ( 5, 1)→( 4, 1)→ 2 ( 9, 2)→( 9, 8)→(10, 8)→(10, 4)→( 2, 4)→ ( 2, 3)→( 7, 3)→( 7, 8)→( 6, 8)→( 6, 5)→ ( 3, 5)→( 3, 2)→( 8, 2)→( 8,10)→( 5,10)→ ( 5, 1)→( 4, 1)→ 3 ( 9, 2)→( 9, 8)→(10, 8)→(10, 4)→( 2, 4)→ ( 2, 3)→( 7, 3)→( 7,10)→( 6,10)→( 6, 5)→ ( 3, 5)→( 3, 2)→( 8, 2)→( 8,10)→( 5,10)→ ( 5, 1)→( 4, 1)→ 4 ( 9, 2)→( 9, 8)→(10, 8)→(10, 4)→( 2, 4)→ ( 2, 3)→( 7, 3)→( 7,10)→( 8,10)→( 8, 2)→ ( 3, 2)→( 3, 5)→( 6, 5)→( 6,10)→( 5,10)→ ( 5, 1)→( 4, 1)→ 5 ( 8, 2)→( 8,10)→(7, 10)→( 7, 3)→( 2, 3)→ ( 2, 4)→(10, 4)→(10, 8)→( 9, 8)→( 9, 2)→ ( 3, 2)→( 3, 5)→( 6, 5)→( 6,10)→( 5,10)→ ( 5, 1)→( 4, 1)→全探索は私の環境のベーシックプログラムは無理のようです。
【問題3】
9 手
1 ( 6,10)→( 6, 5)→( 1, 5)→( 1, 8)→(10, 8)→ (10, 1)→( 1, 1)→( 1, 2)→( 9, 2)→ 2 ( 6,10)→( 6, 5)→( 1, 5)→( 1, 8)→(10, 8)→ (10, 2)→( 1, 2)→( 1, 1)→(10, 1)→ 3 ( 6,10)→( 6, 5)→( 1, 5)→( 1, 2)→(10, 2)→ (10, 8)→( 1, 8)→( 1, 1)→(10, 1)→ 4 ( 6,10)→( 6, 5)→( 2, 5)→( 2, 2)→(10, 2)→ (10, 8)→( 1, 8)→( 1, 1)→(10, 1)→ 5 ( 9, 2)→( 1, 2)→( 1, 1)→(10, 1)→(10, 8)→ ( 1, 8)→( 1, 5)→( 6, 5)→( 6,10)→ 6 (10, 1)→( 1, 1)→( 1, 2)→(10, 2)→(10, 8)→ ( 1, 8)→( 1, 5)→( 6, 5)→( 6,10)→ 7 (10, 1)→( 1, 1)→( 1, 8)→(10, 8)→(10, 2)→ ( 2, 2)→( 2, 5)→( 6, 5)→( 6,10)→ 8 (10, 2)→( 1, 2)→( 1, 1)→(10, 1)→(10, 8)→ ( 1, 8)→( 1, 5)→( 6, 5)→( 6,10)→最短は9手で8通りのようです。
【青木コメント】
プログラムで迫ってくださいました。
◆東京都 You.O さんからの解答
最短手数ではないかもしれません。
【問題1】 16手
(1,3)→(6,3)→(6,4)→(2,4)→(2,5)→
(6,5)→(6,10)→(2,10)→(2,6)→(3,6)→
(3,2)→(6,2)→(6,1)→(4,1)→(4,6)→(10,6)
【問題2】 22手
(6,4)→(6,10)→(5,10)→(5,1)→(4,1)→
(4,2)→(3,2)→(3,3)→(2,3)→(2,4)→
(3,4)→(3,5)→(4,5)→(4,3)→(7,3)→
(7,10)→(8,10)→(8,2)→(9,2)→(9,8)→
(10,8)→(10,4)
【問題3】 9手
(9,2)→(1,2)→(1,1)→(10,1)→(10,8)→
(1,8)→(1,5)→(6,5)→(6,10)
次の操作は必ず最初に行う必要があることがわかります。
《1》
ある1個の碁石Aに着目したとき、その上下左右のうち1方向にしか他の碁石がない場合、その方向にあって碁石Aに最も近い碁石BをAと線分で結ぶ。
このとき、碁石Aがスタート地点またはゴール地点になる。
3個以上ある場合、「碁石拾い」のルールにしたがった手順を見つけることはできない。
(「一筆書き」の"奇点"と同じですね)
《2》
ある1個の碁石Pに着目したとき、その上下左右のうち2方向にしか他の碁石がない場合、それぞれの方向にあって碁石Pに最も近い碁石QおよびRをPと線分で結ぶ。
※ 操作《1》で碁石Aに相当するものが2個見つからなかった場合、この段階で場所のわかっていないスタート地点およびゴール地点にある碁石については、《2》の操作は必ずしも必要ではないのですが、答えを見つける手がかりとしてこの操作を行ったあとでスタート地点およびゴール地点を決定するほうがよいでしょう。
【問題1】
操作《1》(碁石A:●,碁石B:●)

操作《2》(碁石P:●,碁石Q・R:●)
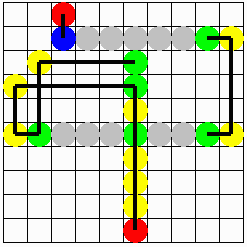
答 え
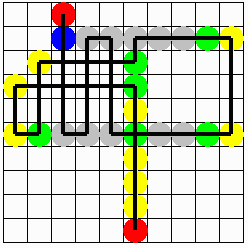
【問題2】
操作《1》で碁石Aに相当するものは見つからない。
操作《2》(碁石P:●,碁石Q・R:●)
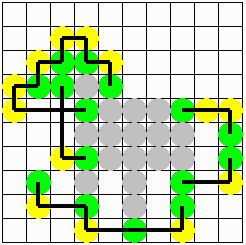
答 え
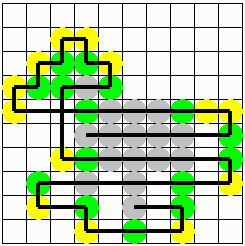
より優れた答え
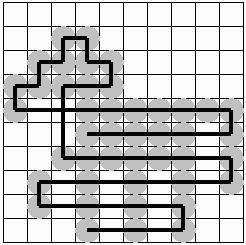
【問題3】
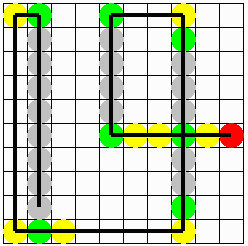
操作《1》(碁石A:●,碁石B:●)
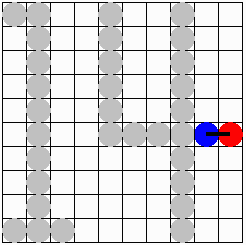
操作《2》(碁石P:●,碁石Q・R:●)
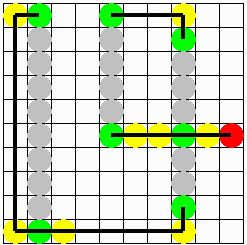
答 え
【青木コメント】
最短でない解もあるのですが、見事に分析してくださいました。
本来、最短か否かはあまり重要ではないでしょう。
◆ 問題へもどる
◆ 今週の問題へ