◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 白
【問題2】(8,1)
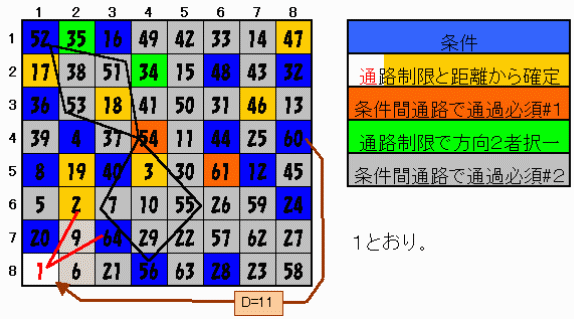
∵下図参照。
(8,1)を通過する通路は赤線で示す1とおりである。
従って(8,1)は64番に隣接するので 63番か1番である。
63番とすると、60番までの距離が長く3回では到達できない。
よって1番である。
【問題3】 下図。1とおり。
∵ 下図参照。
問題2のような考え(黄色)と、条件(青)間の可能な通路中選択の余地が無いもの(橙色){例:54番と黒線}で絞込む。
行き詰まったところで、34番35番(緑)のところでもう一つの可能性である、37番38番と2者択一となる。
それぞれを(橙色)に同じく必須通過点(灰色)で絞り込むと後者は矛盾があり、一方前者は図の1通りが残った。

【感想】
問題3は手ごわかった。
◆千葉県 なのはな子 さんからの解答
【問題1】
ナイトの動き方から考えて、黒のマス目が偶数回なら、白のマス目は奇数回になります。
だから出発点「1」は、白のマス目です。
【問題2】
ナイトの動き方から考えて、
(8,1)は「1」か「63」のどちらかであるとわかります。
しかし、「64」と「60」の位置からみて「63」ではありえません。
だから、(8,1)が出発点「1」です。
【問題3】
(8,1)→(6,2)→(5,4)→(4,2)→(6,1)→
(8,2)→(6,3)→(5,1)→(7,2)→(6,4)→
(4,5)→(5,7)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(3,3)→(5,2)→(7,1)→
(8,3)→(7,5)→(8,7)→(6,8)→(4,7)→
(6,6)→(7,8)→(8,6)→(7,4)→(5,5)→
(3,6)→(2,8)→(1,6)→(2,4)→(1,2)→
(3,1)→(4,3)→(2,2)→(4,1)→(5,3)→
(3,4)→(1,5)→(2,7)→(4,6)→(5,8)→
(3,7)→(1,8)→(2,6)→(1,4)→(3,5)→
(2,3)→(1,1)→(3,2)→(4,4)→(6,5)→
(8,4)→(7,6)→(8,8)→(6,7)→(4,8)→
(5,6)→(7,7)→(8,5)→(7,3)
◆宮城県 アンパンマン さんからの解答
【問題1】
白、黒、白、黒、...の順番で移動しているので、偶数は黒のため、奇数である1は白のマス目です。
【問題2】
ループであるため(8,1)からは(6,2)あるいは64から一つの移動で離れています。
(8,1)は63あるいは1ですが、63だと1から離れすぎて、1しかなりません。
よって、出発点は(8,1)です。
【問題3】
(8,1)→(6,2)→(5,4)→(4,2)→(6,1)→
(8,2)→(6,3)→(5,1)→(7,2)→(6,4)→
(4,5)→(5,7)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(3,3)→(5,2)→(7,1)→
(8,3)→(7,5)→(8,7)→(6,8)→(4,7)→
(6,6)→(7,8)→(8,6)→(7,4)→(5,5)→
(3,6)→(2,8)→(1,6)→(2,4)→(1,2)→
(3,1)→(4,3)→(2,2)→(4,1)→(5,3)→
(3,4)→(1,5)→(2,7)→(4,6)→(5,8)→
(3,7)→(1,8)→(2,6)→(1,4)→(3,5)→
(2,3)→(1,1)→(3,2)→(4,4)→(6,5)→
(8,4)→(7,6)→(8,8)→(6,7)→(4,8)→
(5,6)→(7,7)→(8,5)→(7,3)
【解説】
まず、定義をします。
定義:移動順序でイのマス目はアのマス目からk回の移動で離れている場合は「イはアのk隣」といいます。
k=1の時は、「イはアの隣」といいます。
【定理1】
各マス目は二つの隣が存在する。
証明:ループであるため。
【定理2】
アの可能な隣はイとウの2つしかない場合、アの隣はイとウになります。
証明:
定理1より、アに移動する前とアからの移動したあとのマス目が必要で、アの隣はイとウしかなりません。
【定理3】
アはウの2隣で、アとウの可能な隣はイ一つしかない場合、イの隣はアとウになります。
証明:
アはウの2隣のため、アとウの間は、一つの隣が必要です。
アとウの可能な隣は一つしかないため、イはアとウの隣にならないといけません。
【定理4】
ア、イ、とウはエのすべての可能隣で、アはウの2隣ではない場合、エの一つの隣はイになります。
証明:
エの隣はアとウ両方ではありえないため、エの一つの隣はイにならないといけません。
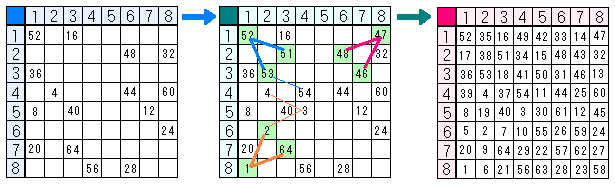
問題2)から1は(8,1)だとわかり、
1の隣は63以外は(6,2)しかないため(6,2)は2で、2と4の隣は(5,4)しかないため、(5,4)は3です。
(8,8)の隣(7,6)と(6,7)です。
問題から与えられた順序は4回移動ずつ離れているため、(7,6)と(6,7)の隣は与えられた順序にしかならないため、(7,6)の隣は56で、(6,7)の隣は60になります。
(6,1)の可能な隣は4、40、64、と(8,2)なのですが、4、40、64は(移動数で)かなり離れているため、(8,2)は(6,1)の隣になり、もう一つの隣は40か64だと考えると、(8,2)は38、42あるいは62になりますが、いずれも、36、44あるいは60から離れすぎるため、(6,1)の隣は4であり、(6,1)は5、(8,2)は6です。
8と6の隣は(6,3)のため、(6,3)は7です。
(1,1)の隣は(3,2)と(2,3)で、(1,8)の隣は(2,6)と(3,7)です。
(3,7)は50だと、52から離れすぎるため、(3,7)は46で、(2,6)は47です。
(2,1)の隣は16と(3,3)です。
(3,2)か(2,3)、どちらか53で、56までに移動できるためには、54が(4,4)にしかなりません。
54と56の唯一の隣である(6,5)は55になります(定理3)。
(7,8)の一つの隣は(6,6)です(定理4)。
28の隣は(7,4)と(7,8)です(定理2)。
(7,4)の隣は28のほかに(5,5)があります(定理2)。
(5,8)の隣は46、44、(6,6)(26あるいは30になる)、と(7,7)であるため、(5,8)は45、43、31、25になる可能性があります。
(5,8)が43だと(7,7)は42になり、(7,7)と40は隣がないためありえません。
31と25も不可能です。
よって、(5,8)は45になります。
(8,7)の一つの隣は(7,5)です(定理4)。
もう一つの隣は(6,6)だと(7,5)は32あるいは24になってしまい、矛盾が生じます。
よって、(8,7)の隣は(7,5)と24です。
さらに(8,7)は23で、(7,5)は22であることがわかります。
(4,7)25です(定理3)。
32の隣は(1,6)と(3,6)です(定理2)。
(1,6)は31だと28から遠すぎるため、(1,6)は33になり、(3,6)は31になります。
よって(5,5)、(7,4)、(7,8)、(6,6)は30、29、27、26の順番になります。
(8,3)は21です(定理3)。
また(5,2)は19になります(定理2)。
よって、(8,5)は63になります(定理2)。
(7,7)は62で、(5,6)は61です(定理2)。
12の隣は(4,5)と(3,8)で(定理2)、(3,8)が11だと8から遠すぎます。
よって、(3,8)は13で、(4,5)は11になります。
(1,7)は14です(定理2)。
よって、(2,5)は15になります(定理3)。
そのため、(2,1)は17で、(3,3)18です。
(7,2)は41、39、あるいは9です。
41だと3隣で44まで移動できる方法がないためありえません。
(7,2)は39だと、(6,4)38で、(4,3)は37ですが、この場合は8の隣は7しかないため矛盾(定理1)。
よって、(7,2)は9で(6,4)は10です(定理3)。
40の隣は(4,1)と(3,4)です(定理2)。
また(4,1)の隣は40と(2,2)です(定理2)。
(2,2)は42だと(3,4)が43になってしまい矛盾です。
したがって(4,1)、(2,2)、(3,4)は39、38、41の順になります。
また(4,3)は37であることがわかります(定理3)。
よって、(1,2)は35になります(定理2)。
(2,4)は34です(定理3)。
(3,2)は51だと3隣で48まで辿りつけないため、(3,2)は53で、(2,3)は51であることがわかります。
(1,5)は42で(定理2)、(2,7)は43です(定理3)。
(3,5)は50で、(1,4)は49です(定理2、3)。
以上でコース再現されました。
◆東京都 You.O さんからの解答
【問題1】
ナイトの位置を平面上の格子点を表す座標(2つの整数値の組)で(m,n)のように表示する。
1回の移動でナイトが点(m',n')に移動したとすると、
(m',n') =(m−2,n−1),(m−2,n+1) (m−1,n−2),(m−1,n+2) (m+1,n−2),(m+1,n+2) (m+2,n−1),(m+2,n+1)の8通りの場合が考えられる。
問題図中の左および上の整数値を順に並べたものを座標として扱うことにすると、白いマス目、黒いマス目は座標の和がそれぞれ奇数、偶数となる。
ナイトが4番目に通ったことを示す"4"の数字が黒いマス目に記されていることから、ナイトの出発点となるマス目すなわち数字"1"が記されるべきマス目の色は白であることがわかる。
なぜなら、ナイトは出発点から3回の移動で"4"のマス目に到達している。
ナイトが1回移動するたびに、ナイトが存在する点の座標の和の偶奇、すなわちマス目の色(白/黒)が変化するため、3回の移動を経るとやはりマス目の色が変化する。
"4"のマス目が黒であるから、出発点となるマス目の色は白である。
【問題2】
上で述べたように、盤の中央付近ではナイトは8方向に移動可能であるが、ここから離れるにしたがってナイトが移動可能な方向は限定され、その数は減少する。
そして、盤の角にある4つのマス目((1,1),(1,8),(8,1),(8,8))についてはナイトが移動可能な方向は2つに限定される。
ナイトが盤のすべてのマス目を巡回して最後に出発点に戻っていることから、ナイトがたどったコースのすべてを折れ線で結ぶと、64コあるすべてのマス目からそれぞれ2本の線分が出ていることになる。
ここで、左下角のマス目(8,1)に着目する。
このマス目から1回の移動で到達することのできるマス目は(6,2),(7,3)の2つであるため、(8,1)のマス目はこれら2つのマス目と線分で結ばれている。
ここで、マス目(7,3)にはナイトが最後に通ったことを示す"64"の数字が記されているため、ナイトがマス目(7,3)を通る直前にマス目(8,1)を通ったとすれば、(8,1)には"63"の数字が記されることになり、マス目(6,2)に"62"の数字が記されることになる。ところが、"60"の数字が記されているマス目は(4,8)であり、ナイトの2回の移動で(4,8)から(6,2)へ移動することは不可能なため、このようなことは起こり得ないことがわかる。
ゆえに、ナイトはマス目(7,3)を通った直後にマス目(8,1)を通っていることになる。
(7,3)はナイトが最後に通ったマス目であり、その直後に出発点に戻っていることから、マス目(8,1)が出発点であることが決定する。
【問題3】
4の倍数の数字が記された問題の図中に、【問題2】で求めた出発点を示す"1"の数字を書き込むと下の図1のようになる。
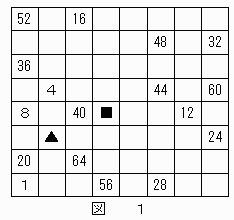
【問題2】でおこなった考察と同様にして、
数字"2"が(6,2)(▲の位置),"3"が(5,4)(■の位置)のマス目に記すことができ、その結果、図2のようになる。
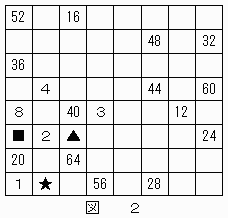
【問題1】でおこなった考察を拡張すると、ナイトの2回の移動による座標の変化のパターンが(ナイトが現在いる地点に再び戻ってくることを含めて)33通りあることがわかる。
図2の★(8,2)は黒いマス目で4の倍数の数字が記されていないことから、
4k−2(kは整数,1≦k≦16)番目にナイトが通ったことがわかる。
ゆえに、ナイトがこのマス目に到達する2つ前および到達した2つ後にナイトがいたマス目には
それぞれ"4(k−1)","4k"の数字が記されているはずである。
ところが、この★のマス目からナイトが2回の移動で到達できる、4の倍数の数字が記されたマス目は、
"4","8","20","28","40","56","64"の7つであり、これらのなかで隣り合った4の倍数は"4"と"8"のみである。
(ナイトの経路がループ状であることを考えると"64"と"4"も条件を満たすが、"2"のマス目がすでに(6,2)に決定しているため、k=1であるとは考えられない。)
したがって、k=2と決定し、★のマス目には"6"の数字が記される。
さらに、▲は"7",■は"5"と決定し、その結果、図3のようになる。
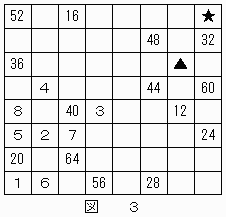
【問題2】と同様に考えると、★のマス目は"47"または"49"となるが、"52"のマス目の位置から★は"47"に決定する。
これにより、▲は"46"となり、結果は図4のようになる。
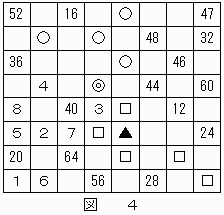
次に"54"が記されるマス目を決定する。
"52","56"のマス目からナイトが2回の移動で到達できるマス目のうち、まだ数字が記されていないマス目をそれぞれ○,□で表すことにより、それらの共通部分となる◎のマス目が"54"であることがわかる。
これにより、▲が"55"となる。結果を図5に示す。
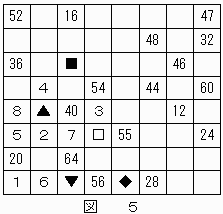
"20"のマス目の位置から、"19"は▲または▼のマス目ということになるが、"16"の位置から▼が"19"ということはあり得ないことがわかる。
したがって、"19"は▲に決定する。
これにより、"18"は□または■ということになるが、同様の考察から"18"は■に決定する。
また、"19"の決定により、"21"は▼,"63"は◆と決定する。
結果を図6に示す。
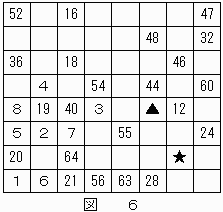
図2と同様の考察を★のマス目について行う。
このマス目からナイトが2回の移動で到達できる、4の倍数の数字が記されたマス目は、位置関係的には
"12","24","28","40","44","56","60","64"の8つであるが、
このうち"12","28","40","56"のマス目には実際には到達できないことがわかる。
残りの"24","44","60","64"のなかで隣り合った4の倍数の組は("60","64")の1通りのみである。
したがって、★のマス目は"62"に決定する。これによって、▲は"61"に決定する。
結果は図7のようになる。
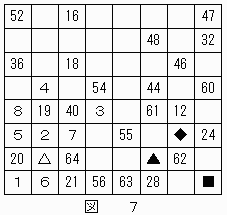
"57"は△または▲ということになるが、△が"57"だとすると、ナイトはここから3回の移動で"60"のマス目へ到達できないため、"57"は▲に決定する。
これにより、■が"58"に、◆が"59"に決定する。
結果を図8に示す。
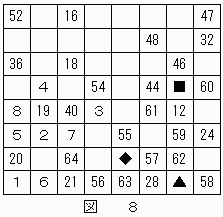
▲と■はそれぞれ"23","25"のいずれかであるが、■が"23"だとするとナイトは"21"のマス目から2回の移動で"23"のマス目へ到達できないため、▲が"23",■が"25"となる。
また、◆は"22"に決定する。
結果は図9のようになる。
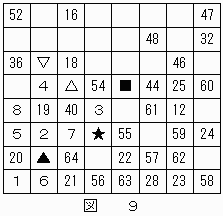
図6と同様の考察を★のマス目について行う。
このマス目からナイトが2回の移動で到達できる、4の倍数の数字が記されたマス目は、位置関係的には
"8","12","20","24","36","40","48","56","60","64"の10通りあるが、
このうち"20","24","60","64"のマス目には実際には到達できないことがわかる。
残りの"8","12","36","40","48","56"のなかで隣り合った4の倍数の組は
("8","12"),("36","40")の2通りである。
ここで、★が"38"であるとすると、△が"37"となり、"9"は▽または▲となる。
ところが、▽は"51"または"53"であり、▲が"9"だとすると★が"37"に決定しているため"10"の数字が記される可能性のあるマス目が存在しなくなってしまう。
したがって、★のマス目は"10"に決定する。
これによって、■は"11"に決定する。
このとき、▲のマス目からナイトが1回の移動で到達できるマス目は"8","40","56"そして"10"の数字が記された★の4つとなるが、このなかで差が2である組は("8","10")の1通りのみである。
よって、▲は"9"に決定する。
結果を図10に示す。
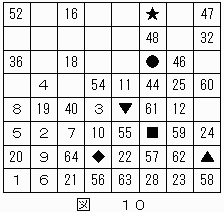
▲と◆はそれぞれ"27","29"のいずれかであるが、▲が"29"だとすると■が"30"となり、ナイトはここから2回の移動で"32"のマス目へ到達できないため、▲が"27",◆が"29"となる。
これにより、■が"26",▼が"30",●が"31"と決定する。
これにより、★は"33"となる。
結果は図11の通り。
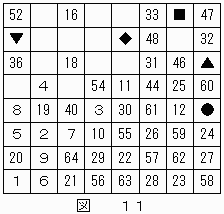
▲が"13",■が"14",◆が"15",▼が"17"に決定する。
これにより、●は"45"となる。
結果を図12に示す。
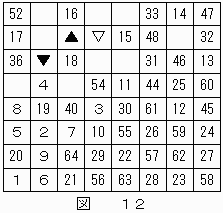
▲と▼はそれぞれ"51","53"のいずれかであるが、▼が"51"だとすると▽が"50"となり、ナイトは"48"のマス目から2回の移動で"50"のマス目へ到達できないため、▲が"51",▼が"53"となる。
結果は図13に示す。
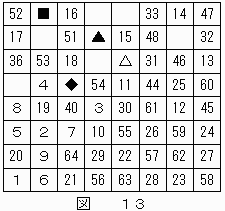
"34"は△または▲のいずれかである。
"34"が△だとすると、"35"は◆,"37"は■,"38"は▲となり、"39"の数字が記される可能性のあるマス目が存在しなくなってしまう。
したがって、"34"は▲と決定する。
このとき、"37"は■または◆のいずれかとなる。
"37"が■だとすると、"38"の数字が記される可能性のあるマス目が存在しなくなってしまう。
ゆえに、"37"は◆となる。
これにより、"35"は■となる。
結果を図14に示す。
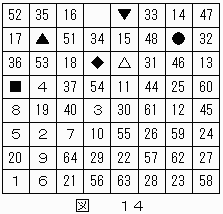
"38"は△または▲のいずれかであるが、"38"が△だとすると、ナイトはここから2回の移動で"40"のマス目へ到達できないため、"38"は▲と決定する。
このとき、"39"は■または◆のいずれかとなる。"39"が◆だとすると、"41"は■となり、"42"の数字が記される可能性のあるマス目が存在しなくなってしまう。
ゆえに、"39"は■となる。
これにより、"41"は◆,"42"は▼,"43"は●となる。
結果を図15に示す。
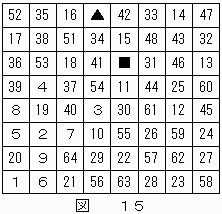
▲が"49",■が"50"に決定する。
結果を図16に示す。
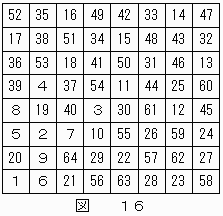
このようにして、ナイトが巡回したコースのすべてが再現できた。
これを座標で表示すると、下のようになる。
<解答>
【問題1】 白のマス目
【問題2】 左下角(8,1)のマス目
【問題3】
(8,1)→(6,2)→(5,4)→(4,2)→(6,1)→
(8,2)→(6,3)→(5,1)→(7,2)→(6,4)→
(4,5)→(5,7)→(3,8)→(1,7)→(2,5)→
(1,3)→(2,1)→(3,3)→(5,2)→(7,1)→
(8,3)→(7,5)→(8,7)→(6,8)→(4,7)→
(6,6)→(7,8)→(8,6)→(7,4)→(5,5)→
(3,6)→(2,8)→(1,6)→(2,4)→(1,2)→
(3,1)→(4,3)→(2,2)→(4,1)→(5,3)→
(3,4)→(1,5)→(2,7)→(4,6)→(5,8)→
(3,7)→(1,8)→(2,6)→(1,4)→(3,5)→
(2,3)→(1,1)→(3,2)→(4,4)→(6,5)→
(8,4)→(7,6)→(8,8)→(6,7)→(4,8)→
(5,6)→(7,7)→(8,5)→(7,3)
◆ 問題へもどる
◆ 今週の問題へ