◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
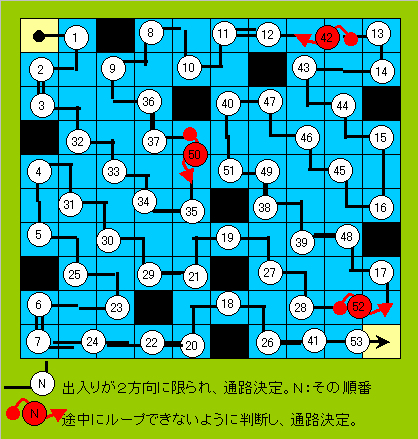
下図参照
【おまけ】
1とおり
∵出入りが2方向に限られ通路が決定するもの、及びループにならない通路の選択を順につめて行くと、下図のようになり、1通りしかなかった。
但し、つめる順(N)は一例。

◆東京都 You.O さんからの解答
まず、亀が進むことができる白のマス目を点で、亀が通る可能性のある、上下左右に隣り合う白のマス目どうしを結ぶ"経路"を点線で表すと、図1のようになる。
(S,Gはそれぞれスタート地点(1,1),ゴール地点(10,10)を表す)
◆図1
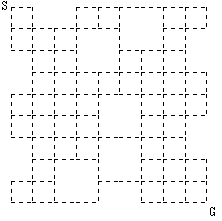
[A]
『亀がすべての点を1回ずつ通ってSからGまで進む経路を図中に表したとき、SおよびGからはそれぞれ1本ずつ、他の87個の点からは各2本ずつ、隣り合う点に至る経路(線分)が描かれている』はずである。
それゆえ、図1でS,G以外の87個の点のうち隣り合う点に至る経路が2本しかないものについては、SからGまで進む過程で必ずその2本の経路を通ることになる。
そこで、このような経路を実線で結ぶと図2のようになる。
◆図2
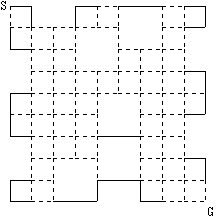
[B]
次に、上の『 』により、図2でS,G以外の87個の点のうち隣り合う点に至る経路がすでに2本(実線で)描かれているものについては、隣り合う点に至るその他の経路はSからGまで進む過程で絶対に通らないことがわかる。
同様にスタート地点Sについても、最初に亀が必ず右隣のマス(1,2)へ移動することがわかるから、Sと下隣のマス(2,1)を結ぶ経路を通ることはない。
このように考えて、亀がSからGまで進む過程で絶対に通り得ない経路を図2から削除すると、図3のようになる。
◆図3
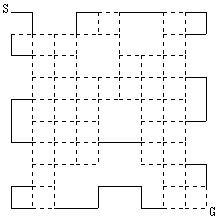
[C]
また、『亀がすべての点を1回ずつ通ってSからGまで進む経路を図中に表したとき、S,G以外の87個の点のうちのいくつかを通るようなループは存在しない』はずである。
そこで、図3に描かれている点線の経路のうち、実線で描くとこのような経路のループができてしまうものを削除する。
その結果を図4に示す。
◆図4
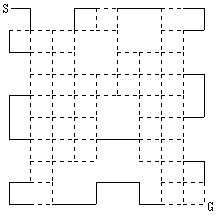
図4に対して[A]と同様の操作を施すと図5のようになる。
◆図5
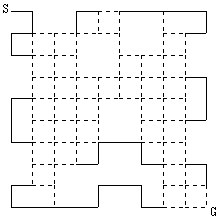
さらに、図5に対して[B]および[C]と同様の操作を順に施すと図6のようになる。
◆図6
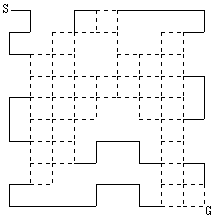
図6に対して[A],[B],[C]と同様の操作を順に施すと図7のようになる。
◆図7
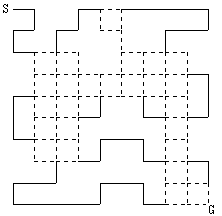
以下、これを順次繰り返すと、図8〜図12のような状態を経て、図13のようになることがわかる。
◆図8
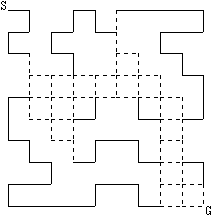
◆図9
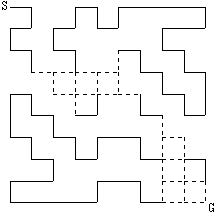
◆図10
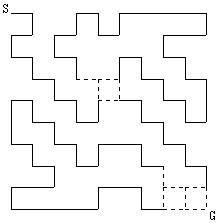
◆図11
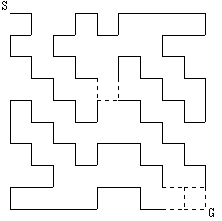
◆図12
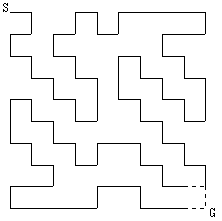
◆図13
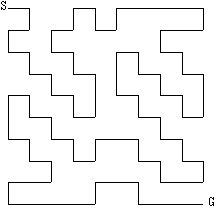
したがって、すべての白いマスを1度ずつ通ってS(1,1)からG(10,10)まで亀が進む経路はただ1通りに決定し、その経路は図13を再び座標で表示し直すことによって得られる。
【問題の解答】
(1,1)→(1,2)→(2,2)→(2,1)→(3,1)→
(3,2)→(4,2)→(4,3)→(5,3)→(5,4)→
(6,4)→(6,5)→(5,5)→(4,5)→(4,4)→
(3,4)→(3,3)→(2,3)→(2,4)→(1,4)→
(1,5)→(2,5)→(2,6)→(1,6)→(1,7)→
(1,8)→(1,9)→(1,10)→(2,10)→(2,9)→
(2,8)→(3,8)→(3,9)→(4,9)→(4,10)→
(5,10)→(6,10)→(6,9)→(5,9)→(5,8)→
(4,8)→(4,7)→(3,7)→(3,6)→(4,6)→
(5,6)→(5,7)→(6,7)→(6,8)→(7,8)→
(7,9)→(8,9)→(8,10)→(9,10)→(9,9)→
(9,8)→(8,8)→(8,7)→(7,7)→(7,6)→
(7,5)→(8,5)→(8,4)→(7,4)→(7,3)→
(6,3)→(6,2)→(5,2)→(5,1)→(6,1)→
(7,1)→(7,2)→(8,2)→(8,3)→(9,3)→
(9,2)→(9,1)→(10,1)→(10,2)→(10,3)→
(10,4)→(10,5)→(9,5)→(9,6)→(9,7)→
(10,7)→(10,8)→(10,9)→(10,10)
【おまけ】
1通り
◆ 問題へもどる
◆ 今週の問題へ