５×５：１０回
【コメント】
おまけについては、Y.M.Ojisan さんからプログラムをいただいたので、探索方法のアイデアを見つけてみてください。
このページの一番下です。
◆岐阜県の中学校２年生 土岐 佳輝 さんからの解答
【問題１】
3手でできます。(8,5)→(7,7)→(5,6)→(7,5)
(8,5)→(6,6)→(8,7)→(7,5)
(8,5)→(7,7)→(5,6)→(7,5)
後はこれの左右対称です。
【問題２】(8,5)→(7,7)→(6,5)→(5,3)→(4,5)→(2,4)→
(3,6)→(5,5)→(6,7)→(7,5)→(5,6)→(3,5)
(8,5)→(6,6)→(4,5)→(5,3)→(6,5)→(7,7)→
(9,6)→(7,5)→(6,3)→(5,5)→(4,7)→(3,5)
(8,5)→(6,4)→(4,5)→(5,7)→(6,5)→(8,6)→
(6,7)→(7,5)→(6,3)→(5,5)→(4,7)→(3,5)
等 11手でした。
【問題３】
まず、進むパターンは4×3×2×1の24通りあります。
一歩ずつ（つまり1・2・3・4の順）進むと(8,5)→
(7,7)→(9,6)→(7,5)→(6,3)→(8,4)→
(6,5)→(5,3)→(7,4)→(5,5)→(4,3)→
(6,4)→(4,5)→(3,3)→(5,4)→(3,5)
15手です。
4・3・2・1でいくと(8,5)→
(6,6)→(4,5)→(2,6)→(4,7)→(5,5)→
(6,3)→(8,4)→(6,5)→(8,6)→(9,4)→
(7,5)→(5,6)→(3,5)
13手です。
これを見るように、隣りあわせのを取りに行く順番は効率的でないことがわかります。
隣に行くにはひとつ離れたところに行くより、1手分ロスしてしまうからです。
(8,5)→(7,7)→(5,6)→(7,5) と (8,5)→(7,7)→(6,5) の差です。
よって、できる限り一つ飛ばしの順で進んだほうがいいとわかります。
ひとつ飛ばしは、１・３と２・４の２種類。
後はどっちを先に持ってくるかの違いですが、１・３を先に持ってくるとロスが増えます。(8,5)→
(7,7)→(9,6)→(7,5)→(6,7)→(5,5)→
(6,3)→(8,4)→(6,5)→(5,7)→(4,5)→
(3,3)→(1,4)→(3,5)
１から行きましたが、１マス移動するプロセスがどうしても３回必要です。
２・４から行くと、(8,5)→
(7,7)→(6,5)→(5,3)→(4,5)→(2,4)→
(3,6)→(5,5)→(6,7)→(7,5)→(5,6)→(3,5)
のように間の１回だけですみます。
よって、２・４の組から始まるパターンの４組が一番手数が少なくてよいと思われます。
【感想】
こういう問題は面白いですよね。
自分で動かせるので、できるとわかりやすいし。
◆岐阜県の小学生 紅葉 さんからの解答
【問題１】
答え 3回 (7,3 4,5 7,5)
これ以外にも、5種類ぐらいある。
理由
1に行くには、3つのことが必要である。
【問題２、３】
答え 11回
(7,7 6,5 5,7 4,5 6,6 8,7 7,5 6,7 5,5 4,7 3,5)
理由
1〜4のますを通り3,5の地点まで行くには、まず2と4のますに行く。
ここで4回の移動が必要となる
次に1のマスに行く。
ここで3回の移動が必要となる。
最後に３を通り3,5のマスに行く。
ここで4回の移動が必要となる。
2と4のマスに最初に行くのは、余分な移動なしで、最初から移動できるためである。
次に1のますに行くのに3回の移動が必要となるのは
2回の移動で1のますに行くには、1と2の行動を1回の移動で行う必要がある。
しかし、1と2の行動を同時に行えるマスは4のマスに行った時点でない。
よって1のマスに行くには3回が最短である。
そして、1のマスから3のますを通り、3,5の地点まで行くには、4回の移動が必要である。
つまり、
４（2を通り4のますに行く）＋３（4のマスから1のマスに行く）＋４（3のますを通り3,5の地点に行く） ＝１１よって11回が最短である。
◆広島県 清川 育男 さんからの解答
【問題１】(8,5)→(7,3)→(5,4)→(7,5)
３ 回
【問題２】(8,5)→(7,3)→(6,5)→(5,7)→(4,5)→(5,3)→
(7,4)→(5,5)→(6,7)→(7,5)→(5,4)→(3,5)
１１ 回
【問題３】
１段おきの場合は２回で移動可能であるが、問題２の場合は３回必要。
２×４+３＝１１が最短手数となる。
【おまけ】
１７回
プログラムを組んでチェックしました。
１７回は回転、裏返しは同一とすれば１個のようです。(6,2)(4,1)(5,3)(6,5)(4,4)
(5,6)(3,5)(1,6)(2,4)(4,5)
(3,3)(5,4)(4,2)(2,1)(1,3)
(3,4)(2,2)(4,3)
１６回は重複が一部ありますが、次の通りです。
６×６ １７回
８×８ ３５回 35 回
1
( 4, 3)
( 2, 2) ( 3, 4) ( 4, 6) ( 2, 5) ( 3, 7)
( 1, 8) ( 2, 6) ( 1, 4) ( 3, 5) ( 2, 3)
( 1, 1) ( 3, 2) ( 5, 1) ( 6, 3) ( 4, 2)
( 5, 4) ( 3, 3) ( 4, 5) ( 5, 7) ( 3, 6)
( 4, 8) ( 6, 7) ( 8, 8) ( 7, 6) ( 6, 4)
( 8, 5) ( 7, 3) ( 8, 1) ( 6, 2) ( 7, 4)
( 5, 3) ( 6, 5) ( 4, 4) ( 5, 6) ( 7, 7)
2
( 4, 3)
( 2, 2) ( 3, 4) ( 4, 6) ( 2, 5) ( 3, 7)
( 1, 8) ( 2, 6) ( 1, 4) ( 3, 5) ( 2, 3)
( 1, 1) ( 3, 2) ( 5, 1) ( 6, 3) ( 4, 2)
( 5, 4) ( 3, 3) ( 4, 5) ( 5, 7) ( 3, 6)
( 4, 8) ( 6, 7) ( 8, 8) ( 7, 6) ( 6, 4)
( 8, 5) ( 7, 3) ( 8, 1) ( 6, 2) ( 7, 4)
( 5, 3) ( 6, 5) ( 7, 7) ( 5, 6) ( 4, 4)
数列サイトを検索してみました。
http://www.research.att.com/~njas/sequences/
ID Number: A003192 (Formerly M1369)
Sequence: 2,5,10,17,24,35
Name: Length of uncrossed knight's path on n X n board.
References L. D. Yarbrough, Uncrossed knight's tours, J. Rec. Math., 1 (No. 3, 1969), 140-142.
Various authors, Uncrossed knight's tours, J. Rec. Math., 2 (1969),154-157.
Links: Illustration of initial terms
E. W. Weisstein, Link to a section of The World of Mathematics. (Currently unavailable)
Keywords: nonn,more,nice
Offset: 3
Author(s): njas◆京都府 としひで さんからの解答
【おまけ】
４×４：５回
５×５：１０回
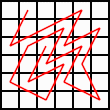６×６：１７回
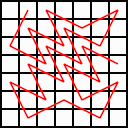７×７：２４回
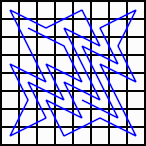８×８：３５回以上
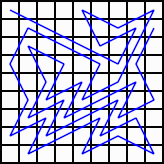９×９：４３回以上
◆愛知県 Y.M.Ojisan さんからの解答
【問題１】
３手 手順は下図
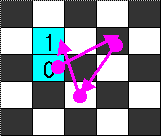
【問題２】
１１手 手順は下図
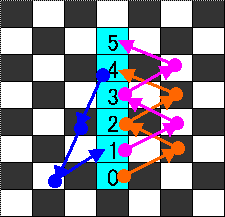
【問題３】
通過／到達しなければならないマス間は、座標（Ｘ、Ｙ）のＸが一定であるから１回では移動できない。
すなわち、最低１０回は必要である｡
この時上図の赤紫→または橙→で示されるようにＹ座標値は偶数か奇数同士しか移動できない。
よって少なくとも一回は青→のような、３回以上の移動が必要である｡
すなわち１１回は最小である｡
【おまけ】
１７手 手順は下図
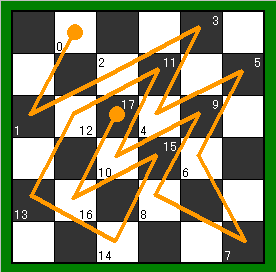
【第１３７回おまけ】 ナイトツアーの探索の方法。
高速ボタン、低速ボタンを押して速度を４段階変えられる。
完成後８秒で再始動する。
◆ 問題へもどる
◆ 今週の問題へ
数学の部屋へもどる