◆広島県 清川 育男 さんからの解答
【問題1】
N=2
3手 2 4 7 4 2 7 4 6 1【問題2】
N=3
5手 6 1 9 5 10【問題3】
N=4
7手 3 10 6 2 7 12 1 3 10 12 6 4 1 13 5 7 2 4 10 8 13 6 10 12 3 5 2 13 7 5 10 8 2 4 13 7 9 4 6 12 10 1 9 1 12 5 8 4 13 9 1 12 8 4 6 13 9 4 12 8 1 5 13 9 4 12 8 13 10 1【おまけ】
N=5
8手 3 7 15 2 10 6 14 1 3 10 15 2 7 5 14 1 3 10 15 6 2 7 14 1 6 13 15 9 5 10 2 16N=6
1個発見しました。
強制的に可能性の高いところに割り込みをかけました。
9手 3 13 18 2 10 14 6 17 1N=7
既知のものからの規則性をもとに12手のものは見つけました。
3,10,21,2,16,6, 20,18,13,9,19,1以上、12手。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 0 0 1 1 2 0 0 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 3 1 2 1 2 1 2 2 3 1 2 3 0 0 3 1 2 3 1 2 3 1 2 3 3 1 3 1 2 1 2 2 3 1 2 3 3 3 3 1 2 3 1 2 3 1 2 0 0 1 4 1 0 0 2 2 3 1 2 3 3 3 3 1 2 3 1 2 3 1 2 2 1 1 5 1 1 2 2 2 3 1 2 3 3 3 3 1 2 3 0 0 3 1 2 2 1 1 6 1 1 2 2 2 0 0 2 3 3 3 3 1 2 3 3 1 3 1 2 2 1 1 7 1 1 2 2 2 2 2 2 3 3 3 3 1 2 3 3 1 3 1 0 0 1 1 8 1 1 2 2 2 2 2 2 3 3 3 3 1 2 3 3 1 0 0 3 1 1 1 9 1 1 2 2 2 2 2 2 3 3 3 3 0 0 3 3 1 1 2 3 1 1 1 10 1 1 2 2 2 2 2 2 0 0 3 3 3 3 3 3 1 1 2 3 1 1 1 11 1 1 2 2 2 2 2 2 2 3 3 3 3 3 3 3 1 1 0 0 1 1 1 12 0 0 2 2 2 2 2 2 2 3 3 3 3 3 3 3 1 1 1 1 1 1 1十進BASIC(最新版)の2進モードで実行してください。
REM 今週の問題−第125回の解答プログラム
REM 1<N<9
SET ECHO "OFF"
LET MAX=20
5 INPUT PROMPT "N=? 1<N<9":N
IF N<2 OR N>8 THEN
GOTO 5
END IF
OPTION BASE 0
DIM A(3*N+4)
DIM T(3*N+2)
DIM C(3*N+2)
DIM M(MAX,3*N+2)
DIM EM(2)
DIM TR(MAX)
REM 使用頻度の高い式の置き換え
LET E1=N-1
LET E2=N+1
LET E3=N+3
LET E4=2*N-1
LET E5=2*N+1
LET E6=3*N-1
LET E7=3*N
LET E8=3*N+1
LET E9=3*N+2
REM 最小手順の検索
REM UTIKIRIの数字はNに応じて変える。N=5の場合にセットしています。
LET T0=TIME
FOR UTIKIRI=6 TO 8
PRINT USING "###":UTIKIRI;
PRINT "手"
REM 初期設定
FOR I=1 TO E7
IF MOD( I , 3) =0 THEN
LET A(I)=3
ELSE
LET A(I)=REMAINDER(I,3)
END IF
NEXT I
LET A(E8)=0
LET A(E9)=0
LET A(E9+1)=0
LET D=0
REM START
REM 初手
LET D=1
FOR I=1TO E6
LET M(1,I)=I
NEXT I
LET T(1)=E6
LET TR(1)=E8
GOTO 20
REM D手目
10 LET D=D+1
REM 打ち切り条件
IF D=UTIKIRI THEN
GOTO 30
END IF
REM 移動する箇所の検索
LET B1=M(D-1,C(D-1))
LET TR(D)=B1
REM 移動出来るポイント
LET TK=0
REM 移動出来ないか繰り返しのポイントの排除
LET B2=TR(D-1)
FOR I=1 TO E8
IF I<>B1 AND I<>B1+1 AND I<>B1-1 AND I<>B2 THEN
LET TK=TK+1
LET M(D,TK)=I
END IF
NEXT I
LET T(D)=TK
20 LET C(D)=C(D)+1
IF C(D)>T(D) THEN
IF D=1 THEN
LET C(D)=0
GOTO 70
ELSE
LET C(D)=0
LET D=D-1
REM 戻す
LET B1=M(D,C(D))
LET B2=TR(D)
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
GOTO 20
END IF
END IF
REM 移動させる
LET B1=M(D,C(D))
LET B2=TR(D)
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
GOTO 10
30 REM 最終局面
REM 移動する箇所の検索
LET TK=0
LET B2=M(D-1,C(D-1))
LET X3=A(B2-1)
LET X4=A(B2+2)
IF B2<>1 AND B2<>2 THEN
LET X1=A(1)
LET X2=A(2)
IF X1=X2 THEN
IF X1=X3 OR X1=X4 THEN
LET TK=TK+1
LET EM(TK)=1
END IF
ELSE
IF X1=X3 AND X2=X4 THEN
LET TK=TK+1
LET EM(TK)=1
END IF
END IF
END IF
IF B2<>E7 AND B2<>E8 THEN
LET X5=A(E8)
LET X6=A(E9)
IF X5=X6 THEN
IF X5=X3 OR X5=X4 THEN
LET TK=TK+1
LET EM(TK)=E8
END IF
ELSE
IF X5=X3 AND X6=X4 THEN
LET TK=TK+1
LET EM(TK)=E8
END IF
END IF
END IF
IF TK=0 THEN
LET D=D-1
REM 戻す
LET B1=M(D,C(D))
LET B2=TR(D)
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
GOTO 20
END IF
40 LET EC=EC+1
IF EC>TK THEN
LET EC=0
LET D=D-1
REM 戻す
LET B1=M(D,C(D))
LET B2=TR(D)
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
GOTO 20
END IF
REM 移動させる
LET B1=EM(EC)
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
REM 出来上がりのチェック
REM 右詰め
IF EM(EC)=1 THEN
FOR I=3 TO E2
IF A(I)<>A(I+1) THEN
GOTO 60
END IF
NEXT I
FOR I=E3 TO E5
IF A(I)<>A(I+1) THEN
GOTO 60
END IF
NEXT I
GOTO 50
END IF
REM 左詰め
FOR I=1 TO E1
IF A(I)<>A(I+1) THEN
GOTO 60
END IF
NEXT I
FOR I=E2 TO E4
IF A(I)<>A(I+1) THEN
GOTO 60
END IF
NEXT I
50 FOR I=1 TO D-1
PRINT USING "###":M(I,C(I));
NEXT I
REM 最終手
PRINT USING "###":EM(EC)
60 REM 戻す
SWAP A(B2),A(B1)
SWAP A(B2+1),A(B1+1)
GOTO 40
70 NEXT UTIKIRI
PRINT TIME-T0
END
◆千葉県 しまだきよこ さんからの解答
VisualBasicでプログラムを組んで調べてみたところ、
【問題3】の解答は10通りありました。
3→10→6→2→7→12→1 3→10→12→6→4→1→13 5→7→2→4→10→8→13 6→10→12→3→5→2→13 7→5→10→8→2→4→13 7→9→4→6→12→10→1 9→1→12→5→8→4→13 9→1→12→8→4→6→13 9→4→12→8→1→5→13 9→4→12→8→13→10→1
| 【問題1】 N=2の場合 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【問題2】 N=3の場合 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【問題3】 N=4の場合 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 3回
4→2→7
【問題2】 5回
6→1→9→5→10
【問題3】 7回
9→4→12→8→13→10→1
【おまけ】
| 多くとも [ | 11N 6 |
] 回 |
| [ | 11N 6 |
] 回の一般的方法がある。 |
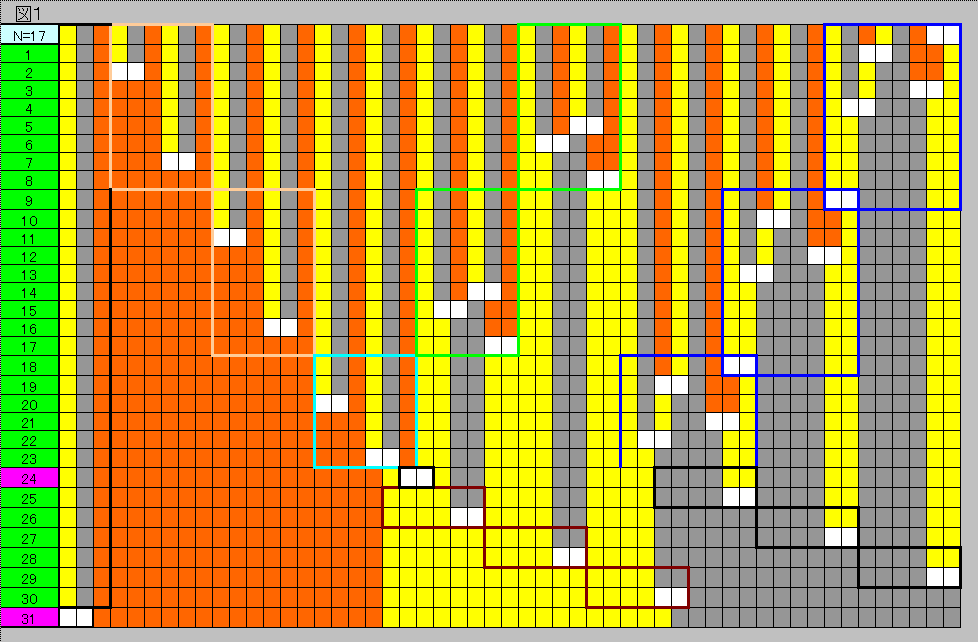
下図1に N=17(mod 6=5)の場合の手順を図示する。
同色枠は同じ手順であり、この反復で
N=5,11,17,...の系列の手順が構成される。
その他のmod値の場合もほぼ同様であり省略する。
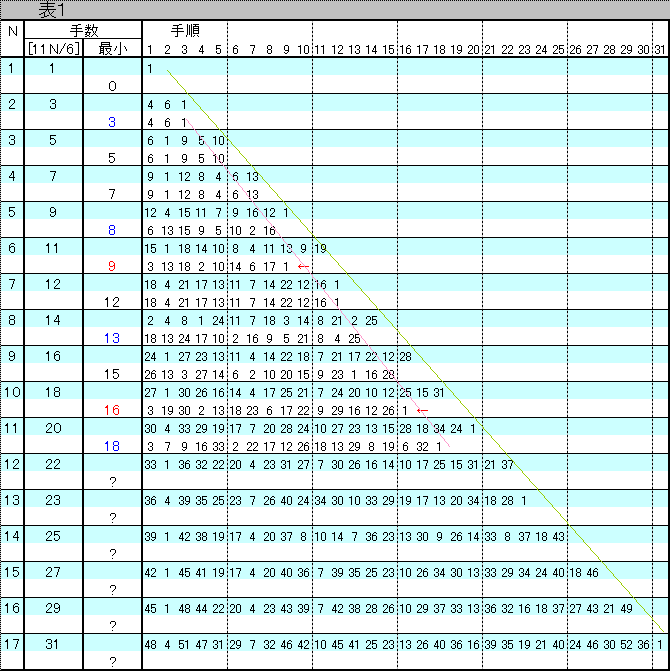
各手順は下表1参照。
しかし、パソコン技で最小を探索すると、実際にはそれより少ない手順が存在する場合がある。
下表1参照。
| N mod 3=2 の場合に [ | 10N 6 |
] の関係が |
【感想】
2N−1であろうとたかをくくっていたら、難問でした。
最終的には1.5N+αのオーダーになるのでしょうか。

◆ 問題へもどる
◆ 今週の問題へ