◆千葉県 しまだきよこ さんからの解答
【問題1】
5→2→8→1 あるいは
2→5→8→1 あるいは
1→7→4→8 あるいは
4→7→2→8
[サンタ=4人、雪だるま=3人] の場合 (4回)
1 2 3 4 5 6 7 8 9 =================== |A|B|A|B|A|B|A| | | =================== |A|B|A|B| | |A|A|B| 1 |A| | |B|B|A|A|A|B| 2 |A|A|B|B|B|A|A| | | 3 | | |B|B|B|A|A|A|A| 4【問題2】
5→2→9→4→1 あるいは
2→9→6→3→10
[サンタ=5人、雪だるま=4人] の場合 (5回)
1 2 3 4 5 6 7 8 9 1011 ======================== |A|B|A|B|A|B|A|B|A| | | ======================== |A|B|A|B| | |A|B|A|A|B| 1 |A| | |B|B|A|A|B|A|A|B| 2 |A|A|A|B|B|A|A|B| | |B| 3 |A|A|A| | |A|A|B|B|B|B| 4 | | |A|A|A|A|A|B|B|B|B| 5【問題3】
7→4→11→6→8→1 あるいは
2→11→6→9→3→12 あるいは
5→8→1→11→4→1 あるいは
5→8→4→11→8→1 あるいは
5→8→11→4→8→1
[サンタ=6人、雪だるま=5人] の場合 (6回)
1 2 3 4 5 6 7 8 910111213 ============================ |A|B|A|B|A|B|A|B|A|B|A| | | ============================ |A|B|A|B|A|B| | |A|B|A|A|B| 1 |A|B|A| | |B|B|A|A|B|A|A|B| 2 |A|B|A|A|A|B|B|A|A|B| | |B| 3 |A|B|A|A|A| | |A|A|B|B|B|B| 4 |A|B|A|A|A|A|A| | |B|B|B|B| 5 | | |A|A|A|A|A|A|B|B|B|B|B| 6【おまけ】
[サンタ=(N+1)人、雪だるま=N人] の場合
最短手数は、(N≧2)の時(N+1)回です。
*(N=1)のときは、1回です。
◆広島県 清川 育男 さんからの解答
【問題1】
1→7→4→8
4回
【問題2】
2→9→6→3→10
5回
【問題3】
2→11→6→9→3→12
6回
左詰め サンタ 6 雪ダルマ 5
2 11 6 9 3 12 3 8 2 11 6 12 6 11 2 9 3 12 11 6 3 8 2 12左詰め 雪ダルマ 5 サンタ 6
右詰め サンタ 6 雪ダルマ 5
2 7 10 5 11 1 10 7 2 5 11 1 11 2 7 4 10 1右詰め 雪ダルマ 5 サンタ 6
3 6 11 2 8 1 5 8 1 4 11 1 5 8 1 11 4 1 5 8 4 11 8 1 5 8 11 4 8 1 7 4 11 6 8 1【おまけ】
N=1のときは1回で例外。
Nのとき (N+1)回が予想されます。
N=5
2,9,6,3,10
N=6
2,11,6,9,3,12
N=7
2,13,10,5,9,3,14
規則性が見られます。
N=7 のとき
0)SDSDSDSDSDSDS□□ 1)S□□DSDSDSDSDSDS 2)SSDDSDSDSDSD□□S 3)SSDDSDSDS□□DDSS 4)SSDD□□SDSSDDDSS 5)SSDDSSSD□□DDDSS 6)SS□□SSSDDDDDDSS 7)SSSSSSSDDDDDD□□
| N=5 | 2 | 9 | 6 | 3 | 10 | ||||||||||||||
| N=6 | 2 | 11 | 6 | 9 | 3 | 12 | |||||||||||||
| N=7 | 2 | 13 | 10 | 5 | 9 | 3 | 14 | ||||||||||||
| N=8 | 2 | 15 | 8 | 11 | 6 | 12 | 3 | 16 | |||||||||||
| N=9 | 2 | 17 | 6 | 11 | 14 | 7 | 12 | 3 | 18 | ||||||||||
| N=10 | 2 | 19 | 6 | 13 | 10 | 17 | 7 | 14 | 3 | 20 |
N≧4
N=4 2,9,6,3,10
N=k 2,2k-1,・・・・・,3,2k ((k+1)個の数列)
(・・・・・)の部分は1通りではないですが、規則性がいまいちですね。
◆宮城県 アンパンマン さんからの解答
【問題1】 4回
1→7→4→8
【問題2】 5回
2→9→6→3→10
5→2→9→4→1
【問題3】 6回
5→8→1→11→4→1
5→8→11→4→8→1
3→8→2→11→6→12
7→4→11→6→8→1
【おまけ】
nが奇数の場合
ABABABABABABABAOOから
AAAAAAAABBBBBBBOOにするには
| n+1 2 |
+ | n+1 2 | =n+1回以上必要です。 |
nが偶数の場合
ABABABABABABAOOから
AAAAAAABBBBBBOOにするには
| n 2 |
+ | n 2 | =n回以上必要です。 |
実際は、n+1回が必要です。(n=2,3,4,5,6,...)
(n=1の場合:1回でできます。)
●n=4kの場合:
2,2n+1,6,2n+5,10,2n+9,...,n-8,n+11,n-2,n+5,
n+2,
n-1,n+6,n-5,n+10,...,3,2n+2
| 合計=2[ | n 4 |
]+1+2[ | n 4 | ]=4k+1=n+1回 |
●n=4k+1の場合:
3,2n-2,7,2n-6,11,2n-10,...,n-6,n+7,n-2,n+3
n-3,n+6,n-7,n+10,...,6,2n-3,2,2n+1,
n+1,2n+2
| 合計=2[ | n-1 4 |
]+2[ | n-1 4 | ]+2=4k+2=n+1回 |
●n=4k+2の場合:
2,2n+1,6,2n+5,10,2n+9,...,n-8,n+11,n-4,n+7,
n+4,n-1,n+3,
n-3,n+8,n-7,n+12,...,3,2n+2
| 合計=2[ | n-2 4 |
]+3+2[ | n-2 4 | ]=4k+3=n+1回 |
●n=4k+3の場合:
3,2n-2,7,2n-6,11,2n-10,...,n-8,n+9,n-4,n+5
n-2,n+4,
n-5,n+7,n-9,n+11,n-13,n+15,..,2,2n+1,
n+1,2n+2
| 合計=2[ | n-3 4 |
]+2+2[ | n-3 4 | ]+2=4k+4=n+1回 |
以上、n+1回で入れ替え可能です。
ちなみに、nが奇数の場合、並んでいる2人の間に空間があってもよいでしたら、n回で移動可能と予想できます。
たとえば、n=5の場合の入れ替えの手順は次のようになります。
3→8→5→11→2
5→8→1→11→4
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 4回
1→7→4→8
2→5→8→1
4→7→2→8
5→2→8→1
【問題2】 5回
2→9→4→8→1
2→9→6→3→10
5→2→9→4→1
【問題3】 6回
2→7→10→5→11→1
2→11→6→9→3→12
3→6→11→2→8→1
3→8→2→11→6→12
5→8→1→4→11→1
5→8→1→11→4→1
5→8→4→11→8→1
5→8→11→4→8→1
6→11→2→9→3→12
7→4→11→6→8→1
10→7→2→5→11→1
【おまけ】
【問題 N=2】 3回
2→5→1
3→5→1
【問題 N=1】 1回
1
【問題 N≧2】 N+1回 より多くない。
N+1回の場合ならば N mod 4 の値により若干異なる4タイプの方法がある。
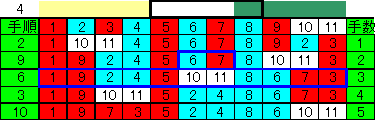
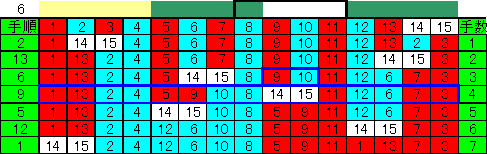
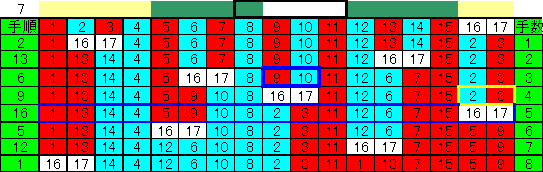
N=2と3の場合は一般解の見通しが分かりにくいのでN=6、7の場合を示した。
(1)
どのタイプも初手は2番
(2-1)
N mod 4 が0〜2の場合は、両側から4個づつ区切り
(1グループだけオーバーラップさせる)、
各グループの中央の2個を外側から互いに交換する。
すると[(N+3)/2]手目で、中央の空白に隣接の1個を除き両側から同種2個ずつまとまった形になる。
ただし、N mod 4=1の場合、最後は2個右にずらした位置を移動する。
(N=5の図黄色枠部)。
(2-2)
N mod 4 が3の場合は、右側2個を別にし、両側から4個づつ区切り
(1グループだけオーバーラップさせる)、
各グループの中央の2個を外側から互いに交換する。
そして[(N+3)/2]手目で右端の2個を移動(N=7の図黄色枠部)すると中央の3個のまとまりを除き、同種2個ずつ左右対称にまとまった形になる。
(3)同種2個の組を中から外へ、左右交換して行く。

◆ 問題へもどる
◆ 今週の問題へ