◆東京都 藤本 さんからの解答
【問題1】
R→K→H→A→L→U→
R→O→H→K→R→O→
D→G→N→Y→R
【問題2】
イ→T→I→A→N→Y→
U→Q→I→T→イ→Q→
F→J→W→コ→イ
【おまけ】
n が 3以上の場合可能
証明は 帰納法で簡単にできます。
証明の手順は 以下のようなものになります。
たとえば 問題2の 6×6の場合には、最初に
イ→Q→U→ウ
と動かして スペースを (5,5)に移せば、問題1と同じ手順で
黒のナイトを (5,5)に持ってこれます。
そのとき スペースは、(4,3) または (3,4)にあります。
スペースが (4,3)のときは
ウ→P→X→イ→Q→U→
ウ→R→V→ケ→X→イ→
Q→U→ク→W→コ→イ
と動かせば 黒のナイトを(6,6)に移せます。
スペースが (3,4)のときも 同様の手順で
黒のナイトを(6,6)へ移動が可能です。
と、これらのことを n と n+1 のチェス版について示せばよいわけです。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
17回
N→E→H→A→L→W→
N→E→H→Q→N→E→
H→K→R→Y→N
【問題2】
17回
イ→Q→I→A→N→J→
F→Q→I→T→イ→Q→
U→J→W→コ→イ
【おまけ】
Nが3以上で全て可能。
∵ 空白の動きもまた騎士と同じであり、騎士と逆に移動すると考えればよい。
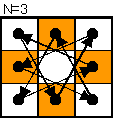
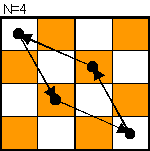
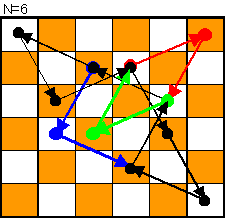
N=3,4,5の場合、下図のようにループになった「騎士回廊」がある。
従って、この回廊を空白が一巡するたびに騎士は逆方向に1個づつ必ずずれるので、いずれ黒騎士も反対側に到達する。
なお、空白だけを移動することが目的の場合、N=5の色付矢印で示される「近道」をすることで,手数の削減が可能。

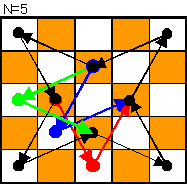
N>5の場合、N=4ないしN=3,5の回廊の半周経路を繋ぎ合わせることにより、「空白」を任意の対角線上に移動が可能である。
(◎=(10) (1)=(7) (2)=(8) (3)=(9) (4)=(10) (5)=(11) 。。。。)即ち,問題のNを3づつ減らすことが可能である。
よって 3以上のNに対して移動可能である。
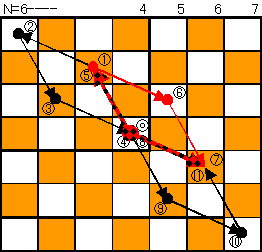
【P.S.】
実際にはN=3の手数は近道が無いのでかなり多く、
N=6で止め、N=6の最小の手順を用いた方が早いようです。
下図参照。
◆宮城県 アンパンマン さんからの解答
【問題1】
17回
R→I→L→A→H→O→
R→I→L→U→R→I→
T→W→N→Y→R
N→Q→H→A→L→U→
R→O→H→K→R→O→
H→E→N→Y→R
【問題2】
17回
W→J→N→A→I→M→
U→J→N→ア→W→J→
U→カ→イ→コ→W
【おまけ】
3*3 の場合、25回で移動可能。
4*4 の場合、5回で移動可能。
n=3i+j (i>1,1≦j≦3) の場合
最初、隅の位置を(2、3)か(3、2)まで移動します。
(3k+j,3k+j)から(3(k-1)+j,3(k-1)+j)に移動するには2回以内で可能です。
j=1の場合(4、4)からあと1回で(2、3)か(3、2)に移動できます。
j=2の場合(5、5)からあと3回で(2、3)か(3、2)に移動できます。
j=3の場合(6、6)からあと3回で(2、3)か(3、2)に移動できます。
次はナイトを移動します。
(3(k-1)+1,3(k-1)+1)から(3k+1,3k+1)に移動するには(隅の位置も考えて)6回以内で可能です。
つまりナイトを(3(i-1)+1,3(i-1)+1)に移動するには
4+6(i-2)回以内で移動可能。
(最初の隅の(ナイトまでの)移動はふくまれていません。)
j=1の場合
(3i+1,3i+1)までは(2i-1)+4+6(i-2)+6=8i-3回以内で移動可能です。
j=2の場合
ナイトを(3i+2,3i+2)までは14回以内で移動可能なので、
(2i+1)+4+6(i-2)+14=8i+7回以内で移動可能です。
j=3の場合
(3i+3,3i+3)までは14回以内で移動可能なので、
(2i+1)+4+6(i-2)+14=8i+7回以内で移動可能です。
◆東京都 BossF さんからの解答
【問題1】
N→C→L→A→H→Q→
N→C→L→W→N→C→
L→U→R→Y→N
【問題2】
W→J→N→A→I→E→
P→ア→N→J→W→ア→
S→O→イ→コ→W
【おまけ】
n≧3でできる
[証明]
例のように左上から右、そして下に1,2,3・・・・・・と番号を振り
各マスを(横.縦)であらわすことにする。
一般に、(1.1)と(n.n)を通る桂馬跳びでつないだループができれば、巡回置換によって題意は達せられることに注意する。
まず、n=1のときは、問題は意味を持たない。
n=2のときは明らかに解なし。
n=3のとき
(1.1)→(3.2)→(1.3)→(2.1)→(3.3)→(1.2)→(3.1)→(2.3)→(1.1)
というループが存在するから可能。
ところで、n≧4のとき
(n.n)→(n-2.n-1)→(n.n-2)→(n-2.n-3)→(n-1.n-1)
というループにより、(n.n)と(n-1.n-1)を通るループが存在し
それらを順次つなげることにより(3.3)まで鎖が出来、これを開けばループとなるから可能である
◆長野県 Mr.D さんからの解答
【問題1】
R→U→L→A→H→E→
N→Y→R→U→L→A→
H→E→N→Y→R→U→
L→A→H→E→N→Y→R
【問題2】
イ→カ→U→Y→N→A→
I→E→P→L→W→コ→
イ→カ→U→Y→N→A→
I→E→P→L→W→コ→
イ→カ→U→Y→N→A→
I→E→P→L→W→コ→
イ→カ→U→Y→N→A→
I→E→P→L→W→コ→
イ→カ→U→Y→N→A→
I→E→P→L→W→コ→イ
【おまけ】
可能です。(n≧3)
(1,1)と(n,n)を通る輪を作ることができれば、ところてんのように移動することができます。
【作り方】
作り方はたくさんあると思いますので、その中の一つをあげます。
1.
壁に沿って、行けるところまで行きます。
(n,n)→(n-2,n-1)→(n-4,n)→(n-6,n-1)→(n-8,n)…
すると、nによって、
(1,n)か(1,n-1)か(2,n)か(2,n-1)のどこかにたどり着きます。
n=4mのときは、(2,n-1)に、
n=4m+1のときは、(1,n)に
n=4m+2のときは、(2,n)に、
n-4m+3のときは、(1,n-1)にたどり着きます。
2.
(1,n-1)か(2,n)にたどり着いた場合は、(3,n-2)に移動します。
そうすると、(1,n)と(n,1)を結ぶ対角線の上に来ました。
3.
そうしたら、これまで移動した線とこれから移動する線が、この対角線について対称になるように
(1,1) まで移動することができます。
4.
今度は、(1,1)と(n,n)を結ぶ対角線について対称になるように
(n,n)まで移動することができます。
これで輪ができました。
こうして作ると同じ場所を2度以上通ることはないので、ところてん方式ができると思います。
最小手順となるとこの手は使えませんが。
◆東京都 未菜実 さんからの解答
【問題1】
遷移図を書いて最短解を捜してみました。
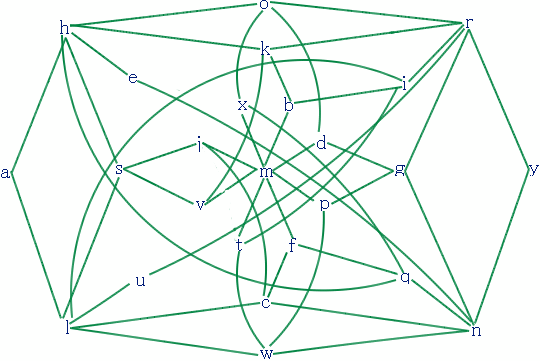
R→O→H→A→L→S→
V→K→H→O→R→K→
H→E→N→Y→R
の17手が最短では?
【問題2】
さすがに図は大変であきらめました。^^;
部分的に最短距離を捜して(図参照)
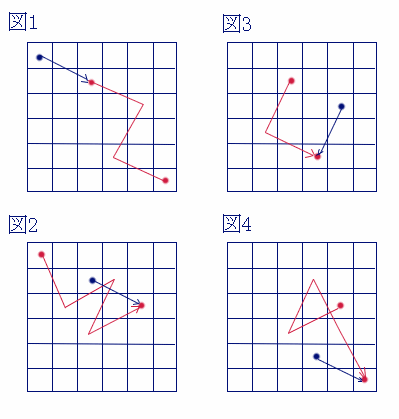
イ→Q→I→A→N→J→
U→Q→I→T→イ→Q→
U→J→W→コ→イ
の 17 手が最短と思います。
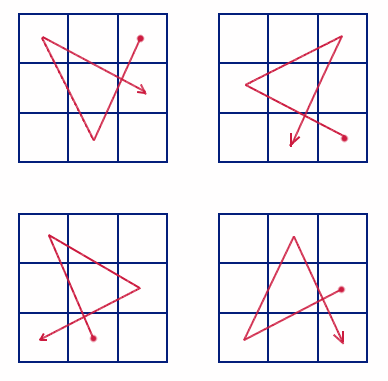
【おまけ】
図の様に上下左右に1つずつ移動できるので必ず一まとまりの遷移図が存在します。
よって必ず解は存在します。
◆ 問題へもどる
◆ 今週の問題へ