『今週の問題』第111回　解答

◆福岡県　古豚 さんからの解答

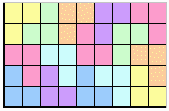
【問題１】

基本図形は、３マスの組み合わせなので、１５個では４５マス。

４５マスを長方形に並べるのは
３×１５、５×９

実際に基本図形を並べてみると、５×９のみ可能

【問題２】

不可能

基本図形１５個では、６０マス。

長方形は
２×３０、　３×２０、　４×１５、
５×１２、　６×１０

いずれも、長方形に１個余るか、
最後の空間が１×４マス　２×２マス、またはＺ形となり、できませんでした。

◆広島県　清川　育男 さんからの解答

【問題１−１】

一辺が１の正方形３個の面積３のタイルとする。

３×１５＝４５
４５＝１×４５＝３×１５＝５×９

短い辺が１のときは明らかに不可能。

短い辺が２のときは、２×３ の最小の長方形が出来る。
このとき、タイルは２個。
１５÷２＝７．５ 不可能。

短い辺が５のときは、可能。５×９

【問題１−２】

５×９の１通り。

【問題２】

不可能。

４×１５＝６０

６０＝１×６０＝２×３０＝３×２０＝４×１５＝６×１０

ロ）
短い辺が２のときは、２×４ の最小の長方形が出来る。
このとき、タイルは２個。
１５÷２＝７．５ 不可能。

ハ）
短い辺が３のときは、３×８ の最小の長方形が出来る。
このとき、タイルは６個。
１５÷６＝２．５ 不可能。

ニ）
短い辺が４のときは、４×４ の最小の正方形が出来る。
このとき、タイルは４個。
１５÷４＝３．７５ 不可能。

ホ）
短い辺が５のときは、ロ）とハ）の組み合わせで、
５×８ の最小の長方形が出来る。
このとき、タイルは１０個。
１５÷１０＝１．５ 不可能。

ヘ）
短い辺が５のときは、ロ）とニ）の組み合わせで、
６×８ の最小の長方形が出来る。
このとき、タイルは１２個。
１５÷１２＝５／３ 不可能。

また、ロ）、ハ）、ニ）、ホ）、ヘ）の組み合わせでも不可能。

◆愛知県　Y.M.Ojisan さんからの解答

【問題１−１】

５×９

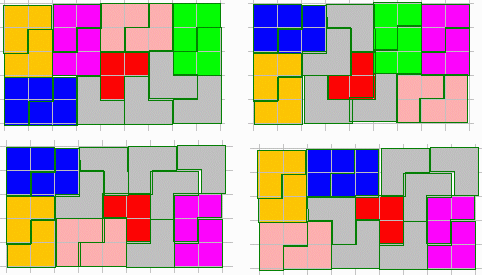
【問題１−２】

１種類。

４５＝１×４５＝３×１５＝９×５
１×はできないのは自明。
３×は　どうしても３×２の倍数にならざるを得ずできない。

【問題２】

６０＝１×６０＝２×３０＝３×２０＝４×１５＝５×１２＝６×１０

◆宮城県　アンパンマン さんからの解答

【問題１−１】

5*9

A A B B C C D D A
A C C B A C D A A
B B C A A B B C C
A B D D C B A D C
A A D C C A A D D 

3*15の場合は作れないので、5*9の長方形しかつくれません。

【問題２】

長方形を作れると仮定します。
できた長方形に1の行と0の行、下の例みたいに交互に書きます。

1 1 1 1 1 1 1 1 1 1 
0 0 0 0 0 0 0 0 0 0 
1 1 1 1 1 1 1 1 1 1  
0 0 0 0 0 0 0 0 0 0  
1 1 1 1 1 1 1 1 1 1  
0 0 0 0 0 0 0 0 0 0

しかし、どんな長方形に対しても1の数は偶数なので、矛盾です。
つまり長方形を作ることができません。

◆愛知県　ピグサス さんからの解答

【問題１−１】

下図のように並べる（同じ文字が１個のタイル）ことにより、
５×９の長方形を作成可能。

１１５５９９ＢＣＣ
１２５７７９ＢＢＣ
２２６６７ＡＡＤＤ
３４４６８０ＡＤＥ
３３４８８００ＥＥ

【問題１−２】

一種類。
５×９の長方形と９×５の長方形は一種類と考える。

証明：

タイルの一辺の長さを１とすると、タイル一個の面積は３であり、
タイル１５枚の面積は４５となる。

面積４５の長方形で一辺の長さが整数となるのは、

１×４５　（４５×１）
３×１５　（１５×３）
５×９　　（９×５）

の３種類しかない。

この３種類の中で、１×４５の長方形は作成不可能であることは明らか。

また、３×１５の長方形にタイルを敷き詰める場合を考える。
長さ３の辺にタイルを敷き詰める方法は、

ＡＡ……
ＡＢ……
ＢＢ……

しかない。
この敷き詰めかたでは、１４個敷き詰めた時に長方形になってしまい、
１５個目のタイルを置いて長方形にする事ができない。
つまり、３×１５の長方形を作成できない。

【問題２】

作成できない

証明：

タイル１５枚で長方形を作成する場合、長方形の面積は６０になる。

面積が６０になる長方形は、

１×６０
２×３０
３×２０
４×１５
５×１２
６×１０

の６通りである。
（上記長方形を９０度回転させた形も実質は同じ）

このうち、１×６０の長方形を作成できないことは明らかであるので、その他の長方形も作成不可能であることを示す。

もとのタイルを１×２のタイル２個に分割すると、
上下に１×１のタイルが２個つながったタイル（以下縦タイルと呼ぶ）と、
左右に１×１のタイルが２個つながったタイル（以下横タイルと呼ぶ）とに、分割できる。

よって、問題のタイルを敷き詰めてできる面積が６０の長方形には
縦タイルが１５個と横タイルが１５個含まれなければならない。

しかしながら、１５個づつ縦タイルと横タイルを含むような長方形を作成できない事は、次の手順で示すことができる。

1. 例として、５×１２のタイルで示す。

2. ５×１２の長方形は、横タイル３０個で敷き詰める事ができる

3. 敷き詰めた横タイルの一部を縦タイルで置き換える事を考える場合、奇数個の横タイルを縦タイルに置き換えることは許されず、 必ず偶数個の横タイルを縦タイルに置き換えなければならない。

4. つまり、横又は縦タイルを敷き詰めて長方形を作成した場合、縦タイルも横タイルも偶数個でなければならない。

5. よって、５×１２の長方形を、１５（奇数）個の横タイルと縦タイルとで敷き詰めることは不可能。

6. 別の長方形の場合でも、横タイル３０個または縦タイル３０個に敷き詰めた状態から置き換る場合を考えることにより、１５個づつの横タイルと縦タイルとで敷き詰めることはできないことが示される。

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる