『中学生からの挑戦状Part９』

『中学生からの挑戦状Part９』解答

◆岩手県　浮浪ぱなしさんからの解答。

【問題１】

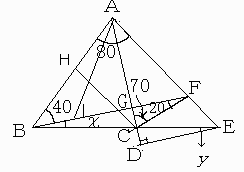
∠ＧＣＦ＝７０°，∠ＧＦＣ＝２０°だから∠ＡＧＦ＝９０°で，
∠ＡＤＥ＝９０°より，同位角が等しいのでＢＦ//ＤＥ。

平行線の錯角は等しいので∠ｘ＝∠ｙである。

以下，∠ｘを求める。

∠ＢＦＡ＝６０°だから，∠ＡＦＣ＝８０°。
Ｃを通りＡＦに平行な線を引き，ＡＢとの交点をＨとすると，四角形ＡＨＣＦは等脚台形となる。
　
線分ＢＦ上に，∠ＦＡＩ＝６０°となる点Ｉを取ると，
△ＡＩＦは正三角形となる。

△ＩＦＣ≡△ＩＡＨより，ＩＣ＝ＩＨ ‥‥‥‥‥‥‥‥(1)
（ＩＦ＝ＩＡ，∠ＩＦＣ＝∠ＩＡＨ，ＦＣ＝ＡＨ）

さて，△ＡＩＧ≡△ＡＦＧより，△ＩＧＣ≡△ＦＣＧとわかるから
△ＩＣＦはＩＣ＝ＦＣの二等辺三角形。

これと(1)から
ＩＣ＝ＩＨ＝ＣＦ＝ＨＡ ‥‥‥‥‥‥‥‥‥‥‥‥‥(2)
であることがわかる。

(2)より，△ＡＨＩはＨＩ＝ＨＡの二等辺三角形。
∠ＩＡＨ＝２０°だから，∠ＡＩＨ＝２０°で，∠ＩＨＢ＝４０°である。
∠ＨＢＩ＝４０°なので，△ＢＩＨはＩＨ＝ＩＢの二等辺三角形。
ＩＨ＝ＩＢと(2)から，△ＩＢＣはＩＢ＝ＩＣの二等辺三角形となる。

∠ＣＦＩ＝２０°だから，∠ＣＩＦ＝２０°なので，∠ＩＢＣ＝１０°

ゆえに，∠ｘ＝１０°である。

この問題は，藤村幸三郎田村三郎著『パズル数学入門』BLUE BACKS にある「未解決のパズル」の１問目の類題ですね。
以前，初等幾何学的に解くのにずいぶん苦労しました。
上記の解答はそのときのものです。(^^;)

それにしても，いったい何をネタにこんな問題を思い付くのでしょう？
これがオリジナル問題だとしたら････すごいセンスだ！

【コメント】

　類題があるとは知りませんでした。
巧妙な補助線で解ける初等幾何の問題もなかなか味がありますね。
入試の直前にこの問題を作っていたのだから、驚いてしまいます。

◆宮城県　アンパンマンさんからの解答。

ABとFCの交差点をM。
BからAFとの平行線をひいてFMとの交差点をN。
ANとBFの交差点をP。

∠CGF＝180-∠GFC-∠GCF=90度からAGはBFの垂直線で
∠CPG＝∠CFG=20度。

∠AFG＝60度から△BPNは正三角形です。
PN＝PB。

∠NPC＝180-∠BPN-∠CPG=100度。
∠PCN＝∠CPG+∠CFG=40度

∠PNC＝180-∠NPC-∠PCN=40度から
PN=PC。

PB=PCと∠BPC=180-∠GPC=160度から
∠PBC＝(180-∠BPC)/2=10度

GFはDEの平行線から
y＝x＝10度