◆山梨県 Footmark さんからの解答。
問題のようにnを整数とすると、
(−10km−1){(−10km−1)+1} も
10kの倍数です。
(ただし、kは1≦k≦3の整数、mは正の整数)
ですから、n=−10km−1
ところが、mはいくらでも大きくできますから、
nの最小値は3問とも −∞
また、「nは正の整数」に置き換えた解答は以下のとおりです。
【問題1】
n = 51 x 1 − 1 = 4
【問題2】
n = 52 x 1 − 1 = 24
【問題3】
n = 53 x 3 = 375
【考え方】
nと(n+1)の差は1です。
ですから,nと(n+1)は1以外に公約数を持ちません。
何故なら1以外にも公約数があると、2数の差はその公約数の倍数になり1にはなりません。
題意より、
n(n+1)=5k2km
(ただし、kは1≦k≦3の整数、mは正の整数)
ですから、2数の一方が 5k2kの因数をすべてを持つ場合と、
2数がそれぞれ 5kと 2kの因数を持つ場合が考えられます。
後者の場合は 5kp と 2kq が2数になります。
(ただし,p,qは1以上の整数で、5kpと2kqは1以外に公約数を持ちません。)
ところが,2数の差は1ですから
5kp=2kq±1 ・・・ (1)
つまり、5kp を 2kで割ると
余りが +1 か −1(結局 2k−1) になるような最小なpを求めることになります。
このように余りが2通りあり、しかも最小値pを求めるには次のようにします。
| 5kp 2k | の余りは 0〜(2k−1) です。 |

【問題3】を例にします。
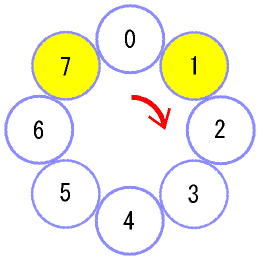
| p=1 とすると、 | 53 23 | の余りは 5 です。 |
そこで、[0]のマスから時計回りに5だけ先に進みます。
pが1増えると、余りはそこからさらに5だけ先に進む筈です。
このことを[1]か[7]のマスになるまで繰り返すことで p が求められます。
すると、目指すマスが1つなら多くとも 2k回で目指すマスになります。
ところが、目指すマスは2つですから多くとも (2k−1)回で目指すマスになります。
この回数が p ですから、p≦2k−1
∴ 5kp≦5k(2k−1)≦5k2k
ですから、一方が 5k2kの因数をすべてを持つ場合よりnは小さい筈です。
到着したマスの数(余り)と回数(p)が分かればnも求められます。
(1)式より、マスの数(余り)が 1の時は
n=2kq=5kp−1、
1でなくて(2k−1)の時は n=5kp
◆東京都 葛衣 奥人 さんからの解答。
「整数」ってことはマイナスも入るはずだけど、小学生の出題だからプラス限定かな?
ちなみにマイナスだと「最小」はマイナス無限大になりそう(笑)
【問題1】
10(=1×2×5)の倍数だから、nとn+1の組み合わせは
1×?と10×?---(1)か
2×?と5×?---(2)という形の数でないといけない。
(1)だと1×11と10×1でn=10
(2)だと2×2と5×1でn=4
ということで、答えはn=4
【問題2】
問題1と同様に考えると、
100=1×2×2×5×5である。
これを「奇数と偶数に分解する」ことになるが
奇数になるのは1か5か25のみである。
というわけで、2つの数は次のいずれかの形で書ける。
(1)1×?と100×?
(2)5×?と20×?
(3)25×?と4×?
(1)だと1×101と100×1でn=100
(2)のくみあわせはありえない
(2つの数の差が1にならない)
(3)だと25×1と4×6でn=24
ということでn=24
【問題3】
問題2と同様に考える。
n=375
◆滋賀県の小学生 西尾 恭史 さんからの解答。
【問題1】
10の約数=1.2.5.10
20の約数=1.2.4.5.10.20
30の約数=1.2.3.5.6.10.15.30
. .
. .
. .
n×(n+1)=10の倍数だから
n=4でO.K.
【問題2】
n×(n+1)=100以上だから
n=10以上
nかn+1が5の倍数にならないといけない。
ここからはあてはめる。
10×11=110・・・・・・×
14×15=210・・・・・・×
・ ・
・ ・
24×25=600・・・・・・O.K
n=24
【問題3】
問題3も問題2と同様にやっていき
n×(n+1)=1000の倍数だから
n=31.622・・・・以上
あてはめていく
34×35=1190
35×36=1260
・ ・
・ ・
375×376=141000
n=375
【コメント】
初歩的な解法でやったら「問題3」にかなり時間を費やしてしまった。
たかがかけ算されどかけ算(?????)
◆茨城県の中学校1年生 田村 昭彦 さんからの解答。
小学生が考えたのだから、n=負の数でないとしておきます。
【問題1】
10の倍数=1×2×5×?=2×5×?ということになる。
つまりn(n+1)の内、どちらかが2の倍数でありどちらかが5の倍数であるということである 。
これをふまえると、nが一番小さくなるためにはn=4となる。
4×5=20
【問題2】
先程と同様にして
100の倍数=1×2×2×5×5×?=2×2×5×5×?
つまりn(n+1)の内
どちらかが5、どちらかが20の倍数かーーー(1)
どちらかが4、どちらかが25の倍数となるー(2)
しかし、(1)の時5の倍数の中に20の倍数も含まれているので、結局(2)とおなじになってしまう。
したがって(2)のとおりだとするとn=24となる。
24×25=600
【問題3】
先程と同様にして
1000の倍数=1×2×2×2×5×5×5×?=2×2×2×5×5×5×?
面倒なので省きますがつまりn(n+1)の内どちらかが125、どちらかが8の倍数となる。
したがってn=375となる。
375×376=141000
「問題3」を前の問題と同じようにn=124としてしまいそうになりました。
とてもおもしろい問題でした。
◆兵庫県 HIPPO さんからの解答。
【問題3】
1000の倍数になる場合、皆さん途中を省略してらっしゃるので、小学生向きの答えを作ってみました。
まず、1000を素因数分解します。
1000=2×2×2×5×5×5
したがって、n(n+1)=2×2×2×5×5×5×M
(Mは正の整数)
右辺を二数の積に書き換えると
n(n+1)=2×500×M
n(n+1)=4×250×M
n(n+1)=8×125×M
n(n+1)=40×25×M
n(n+1)=200×5×M
の5通りが考えられます。
Mも二つに分けることができます。
例えば 6=1×6、2×3・・・のように。
M=P×Q (P、Qはともに正の整数)とすると上の5つの式は
n(n+1)=2×P×500×Q
n(n+1)=4×P×250×Q
n(n+1)=8×P×125×Q
n(n+1)=40×P×25×Q
n(n+1)=200×P×5×Q
と書き換えることができます。
これを文章で表すと、
(A)n(n+1)の二数は、一方が2の倍数 且つ 他方が500の倍数
(B)n(n+1)の二数は、一方が4の倍数 且つ 他方が250の倍数
(C)n(n+1)の二数は、一方が8の倍数 且つ 他方が125の倍数
(D)n(n+1)の二数は、一方が40の倍数 且つ 他方が25の倍数
(E)n(n+1)の二数は、一方が200の倍数 且つ 他方が5の倍数
となります。
ところが、n(n+1)は偶数×奇数なので(A)(B)はこの条件に反します。
(偶数同士の積になっています)
したがって(C)(D)(E)を検証していきます。
(C)
125の整数倍は一の位が0または5が条件。
n=8Pとすると n+1=8P+1
Pの一の位が3または8の時、8P+1の一の位が5となるので125の倍数になる可能性が存在する。
n+1=8Pとすると n=8P−1
Pの一の位が2または7の時、8P−1の一の位が5となるので125の倍数になる可能性が存在する。
次に8の整数倍は偶数。
n=125Qとすると n+1=125Q+1
Qが奇数のとき125Q+1は偶数となり8の倍数になる可能性が存在する。
n+1=125Qとすると n=125Q−1
Qが奇数のとき125Q−1は偶数となり8の倍数になる可能性が存在する。
(D)
25の整数倍は一の位が0または5が条件。
n=40Pとすると n+1=40P+1
一の位は必ず1なので条件に反する。
n+1=40Pとすると n=40P−1
一の位は必ず9なので条件に反する。
次に40の整数倍は一の位が必ず0が条件。
n=25Qとすると n+1=25Q+1
一の位は必ず1か6なので条件に反する。
n+1=25Qとすると n=25Q−1
一の位は必ず4か9なので条件に反する。
(E) これは(D)の場合が適用できるのでダメ。
結局(C)の場合のみ考慮すればよい。 上述したように125の奇数倍のみを考えればよいので、以下となる。
n=125 n+1=126
126は8の倍数ではない。
n=375 n+1=376
376は8の倍数。
n(n+1)=141000 (1000の倍数)
次に
n+1=125 n=124
124は8の倍数ではない。
n+1=375 n=374
374は8の倍数ではない。
n+1=625 n=624
624は8の倍数。
n(n+1)=390000 (1000の倍数)
取り得るnの最小の数値は 375.