『大相撲本場所』解答

◆広島県　清川　育男　さんからの解答。

【問題１】

　ちょっといい気分で問題にのぞんでいます。気分は乗っているのですが。
ズバリ、フィボナッチですね。
階差数列はズバリです。

2		3		5		8		13		21		34		55		89		144		233		377		610		987		1597
	1		2		3		5		8		13		21		34		55		89		144		233		377		610

　答え　１５９７通り

【問題２】

ａ₁=２，ａ₂=３

ａ_n+2＝ａ_n+1＋ａ_n

ヨッシーさんが以前、特性方程式から一般式を求めておられたので詳細は省略します。

【コメント】

　いつもながら鮮やかですね。
確認はしていないのですが、急いで計算してみたら一般項は

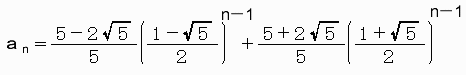
ですね。たぶん。

◆岐阜県立海津北高等学校情報処理科２年生からの解答。

初日
　○
　×・・・２通り

二日目
　○○
　○×
　×○・・・３通り

三日目
　○○○
　○○×
　○×○
　×○○
　×○×・・・５通り

四日目
　○○○○
　○○○×
　○○×○
　○×○○
　○×○×
　×○○○
　×○○×
　×○×○・・・８通り
　　　　　・
　　　　　・
　　　　　・
三日目を見てみると、初日と二日目の合計（２通り＋３通り）で５通り、
四日目を見てみると、二日目と三日目の合計（３通り＋５通り）で８通りとなることより、当日の結果は一昨日と昨日の合計ということがわかり

初日　　　→　　　２通り
二日目　　→　　　３通り
三日目　　→　　　５通り
四日目　　→　　　８通り
五日目　　→　　１３通り
六日目　　→　　２１通り
七日目　　→　　３４通り
八日目　　→　　５５通り
九日目　　→　　８９通り
十日目　　→　１４４通り
十一日目　→　２３３通り
十二日目　→　３７７通り
十三日目　→　６１０通り
十四日目　→　９８７通り
千秋楽　　→１５９７通り

別解：
×（負けの数）で場合分けします。（でも、同じ考えですが）
×をｋ個（ｋ≧０）のとき、○（１５−ｋ）個です。
ただし、ｋ≧９のときは、明らかに不適。

ｋ＝０のとき、○のみで１通り
ｋ＞０のとき、×の起こりうる日は○両端及び間の

　１５−ｋ＋１＝１６−ｋ

よって、×の起こる日は_16-kＣ_k
（ｋ＝１，２，３，・・・，８）

したがって、その総数は

１＋₁₅Ｃ₁＋₁₄Ｃ₂＋₁₃Ｃ₃＋₁₂Ｃ₄＋・・・＋₉Ｃ₇＋₈Ｃ₈
＝１５９７

大相撲の星取表の中やパスカルの三角形の表の中の斜めの和がフィヴォナッチ数列として隠されていることに驚きを感じました。

【コメント】

このコンビネーションの総和から、前述の一般項がでてくるのは何とも不思議です。
何かうまい計算方法があるのでしょうか。

◆岐阜県　水の流れ　さんからの解答。

問題 　参考図のようなパスカルの三角形（二項係数）を斜めに足すと、フィボナッチ数列になることを証明せよ。

＜参考図＞　パスカルの三角形（二項係数）

Ｃ(ｎ,ｒ）	０	１	２	３	４	５	６	７
０	１
１	１	１
２	１	２	１
３	１	３	３	１
４	１	４	６	４	１
５	１	５	１０	１０	５	１
６	１	６	１５	２０	１５	６	１
７	１	７	２１	３５	３５	２１	７	１
８	１	８	２８	５６	７０	５６	２８	８

＜証明＞
　フィボナッチ数列をＦ(ｎ)とすると，
Ｆ(１)＝１，Ｆ(２)＝１ ，Ｆ（３)＝１＋１＝２，
Ｆ（４)＝１＋２＝３， Ｆ（５)＝１＋３＋１＝５，・・・，

『１型』 Ｆ(ｎ＋１)＝nＣ0＋n-1Ｃ1＋n-2Ｃ2＋・・mＣm Ｆ(ｎ＋２)＝n+1Ｃ0＋nＣ1＋n-1Ｃ2＋・・m+1Ｃm ただし、ｎ＝２ｍで、ｍ≧１、ｎ≧２の自然数とする。２つ組で考える。

『２型』 Ｆ(ｎ＋１)＝nＣ0＋n-1Ｃ1＋n-2Ｃ2＋・・mＣm-1 Ｆ(ｎ＋２)＝n+1Ｃ0＋nＣ1＋n-1Ｃ2＋・・mＣm ただし、ｎ＝２ｍ−１で、ｍ≧１、ｎ≧１の自然数とする。２つ組で考える

次に、『１型』のタイプを数学的帰納法で証明します。

Ｆ(１)＝１，Ｆ(２)＝１の条件のもとで，
［１］ｍ＝１のとき、
　　Ｆ（３)＝１＋１＝２，Ｆ（４)＝１＋２＝３ となり、成立。

［２］ｍ＝ｋのとき（ｎ＝２ｋ、ｋは自然数））、成り立つと仮定とすると、すなわち、下の関係が成り立つ。
＜ただし、_nＣ₀＝_nＣ_n＝１である＞

Ｆ(２ｋ＋１)＝2kＣ0＋2k-1Ｃ1＋2k-2Ｃ2＋・・・＋kＣk Ｆ(２ｋ＋２)＝2k+1Ｃ0＋2kＣ1＋2k-1Ｃ2＋・・・k+1Ｃk

ここで、ｍ＝ｋ＋１（ｎ＝２ｋ＋２）を考える。
組み合わせの性質：

_n+1Ｃ_r＝ _nＣ_r-1＋ _nＣ_rより 上の囲みの２式をたすと、

2k+1Ｃ0＋2kＣ0＋2kＣ1＋ 2k-1Ｃ1＋2k-1Ｃ2＋・・＋k+1Ｃk-1＋k+1Ｃk＋kＣk

＝１＋2k+1Ｃ1＋2kＣ2＋・・＋k+2Ｃk＋１

＝2k+2Ｃ0＋2k+1Ｃ1＋2kＣ2＋・・＋k+2Ｃk＋k+1Ｃk+1

＝Ｆ(２ｋ＋３)

次ぎに，『２型』のタイプを数学的帰納法で証明します。

Ｆ(１)＝１，Ｆ(２)＝１の条件のもとで，
［１］ｍ＝１のとき、Ｆ（４)＝Ｆ（２)＋Ｆ（３)＝１＋２＝３ となり、成立。

［２］ｍ＝ｋのとき（ｎ＝２ｋ−１、ｋは自然数））、成り立つと仮定とすると、
　すなわち、下の関係が成り立つ。
＜ただし、_nＣ₀＝_nＣ_n＝１である＞

Ｆ(２ｋ)＝2k-1Ｃ0＋2k-2Ｃ1＋2k-3Ｃ2＋・・・＋kＣk-1 Ｆ(２ｋ＋１)＝2kＣ0＋2k-1Ｃ1＋2k-2Ｃ2＋・・・kＣk

ここで、ｍ＝ｋ＋１（ｎ＝２ｋ＋２）を考える。
組み合わせの性質：
_n+1Ｃ_r＝ _nＣ_r-1＋ _nＣ_rより 上の囲みの２式をたすと、

2kＣ0＋2k-1Ｃ0＋2k-1Ｃ1＋2k-2Ｃ1＋2k-2Ｃ2＋＋…＋kＣk-1＋kＣk

＝１＋2kＣ1＋2k-1Ｃ2＋・・・＋k+1Ｃk

＝2k+1Ｃ0＋2kＣ1＋2k-1Ｃ2＋・・＋k+1Ｃk

＝Ｆ(２ｋ＋２)

◆東京都　鳳　奥人　さんからの解答。

【問題１】

負け数は最大８回ですね。

このとき、勝ち星を○、負け星を●とすると、
●○●○●・・・●○●という成績になっています。

(15-k)勝ｋ敗(0≦ｋ≦8)だったとすると、

|○|○|○|・・・|○|○|○|

この16-k(＝(15-k)+1)個の「|」の中から、●を入れる場所をｋ個選べばよい。

つまり _16-kＣ_k 通り。

７勝８敗→ ₈Ｃ₈＝ 1
８勝７敗→ ₉Ｃ₇＝ 36
９勝６敗→₁₀Ｃ₆＝210
10勝５敗→₁₁Ｃ₅＝462
11勝４敗→₁₂Ｃ₄＝495
12勝３敗→₁₃Ｃ₃＝286
13勝２敗→₁₄Ｃ₂＝ 91
14勝１敗→₁₅Ｃ₁＝ 15
15勝０敗→₁₆Ｃ₀＝ 1

合計　1597通り

【問題２】

１）ｎが奇数の場合

問題１と同様に考える。

まず、負け数は最大

n+1 2

である。

（そのときの星は●○●○●・・・●○●○●となる）

(n-k)勝ｋ敗(0≦ｋ≦

n+1 2

)だったとし、

勝ち星を○、負け星を●とすると

|○|○|○|・・・|○|○|○|

この(n-k+1)個の「|」の中から、●を入れる場所をｋ個選べばよい。

つまり_n-k+1Ｃ_k 通り。

だから答えは

(n+1)/2 Σ k=0

n-k+1Ｃk　通り。

２）ｎが偶数の場合

負け数は最大

n 2

となる。

（星は●○●○・・・●○●○または○●○●・・・○●○●）

(n-k)勝ｋ敗(0≦ｋ≦

n 2

)だったとし、

勝ち星を○、負け星を●とすると

|○|○|○|・・・|○|○|○|

この(n-k+1)個の「|」の中から、●を入れる場所をｋ個選べばよい。

つまり _k+1Ｃ_k 通り。

だから答えは

n/2 Σ k=0

n-k+1Ｃk　通り。

◆山梨県　Footmark　さんからの解答。

【問題１】

勝ちを○、負けを×で１５日間表すと、１５日目がｘの場合もある。
そこで、１６日目を付け加えて○とする。

すると、○を踏んだ段、×を踏まなかった段と解釈すれば、「１度に２段まで上がることを許した、１６段の階段の上がり方」と一緒。

これなら、フィボナッチ数列になることが容易に理解できる。

１段目まで１通り、２段目まで２通り故、フィボナッチ数列(１,２,３,５,８,‥)の１６番目である。

【答え】　１５９７通り

【問題２】

【問題１】と同様に、フィボナッチ数列(１,２,３,５,８,‥)の(ｎ＋１)番目。

本来のフィボナッチ数列(１,１,２,３,５,‥)のｎ番目と比べると、前が１つ後ろが１つの計２つずれている。
それ故、本来のフィボナッチ数列の一般式(証明は省略)のｎを(ｎ＋２)に差し替えればよい。

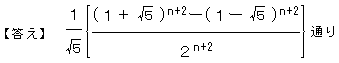
◆東京都　かえる　さんからの解答。

【問題１】

ｋ日目までに連敗していない場合の数をａ(ｋ）

このうち
ｋ日目に勝っている場合の数をｂ(ｋ)
ｋ日目に負けている場合の数をｃ(ｋ)

とおく。
(つまり、ａ(ｋ)＝ｂ(ｋ)＋ｃ(ｋ)・・・(１))

ここで、

ｂ(ｋ＋１)＝ｂ(ｋ)＋ｃ(ｋ)・・・(２)
ｃ(ｋ＋１)＝ｂ(ｋ)・・・(３)

に注意すれば、

　ａ(ｋ＋２)
＝ｂ(ｋ＋２)＋ｃ(ｋ＋２)　(∵(１))
＝ｂ(ｋ＋１)＋ｃ(ｋ＋１)＋ｂ(ｋ＋１)　(∵(２)(３))
＝ｂ(ｋ＋１)＋ｃ(ｋ＋１)＋ｂ(ｋ)＋ｃ(ｋ)　(∵(２))
＝ａ(ｋ＋１)＋ａ(ｋ)　(∵(１))

ａ(１)＝２，ａ(２)＝３なので、・・・以下略

　『大相撲本場所』へ

　数学の部屋へもどる