◆宮城県 甘泉法師 さんからの解答。
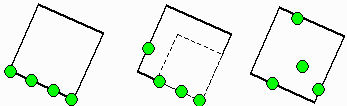
与えられた4点P、Q、R、Sを線分で結び4角形をつくる。
4角形PQRSの各辺の中点を求め、中点を中心とし辺の長さの直径で四角形の外側に半円を描く。
辺PQを直径とする半円上の頂点をA、辺QRを直径とする半円上の頂点をB、辺RSを直径とする半円上の頂点をC、辺SPを直径とする半円上の頂点をDとする。
題意からA、B、C、Dを適当に選べば
線分AQB=BRC=CSD=DPAになる。
点Aを任意にとり線分AQBと線分APDを引き、長さを比べる。
両線分の長さが同じになるように点Aの位置を調整する。
求める点A、B,C,Dが得られる。
補足:この方法では誤差を0にするには無限回の作図が必要です。
◆三重県 いわし さんからの解答。
まず4点の凸包が四角形であることが必要です。
4点を反時計回りにA,B,C,Dとします。
(1) 四角形AEBDが平行四辺形となる点Eを作図
(2) AE=AF, ∠EAF=90°となる点Fを作図
(A,E,Fが反時計回りに並ぶように)
します。
FとCが異なるとき、直線CFをkとおいて
「A,B,Dのkへの射影をA',B',D'とすると、A',Cが線分B'D'に含まれ、A,B,C,Dのkに垂直な直線への射影をA",B",C",D"とすると、 B",D"が線分A"C"に含まれる」...(*)
ことが必要で、
(3) Aを通りkに平行な直線、B,Dを通りkに垂直な直線を作図
すれば、求める正方形が構成できます。
FがCに一致する(すなわちAC⊥BD, AC=BD)ときは、Cを通る直線kを(*)を満たすように任意に引いて、(3)の 操作を行えばOKです。
それから、「作図」とは、有限回の操作で終了するもののことを言います。
無限回の操作を許せば、任意の角の三等分さえ可能になってしまいます。
◆愛知県 Y.M.Ojisan さんからの解答。
4点をA,B,C,Dとします。
4点の状態は、つぎの4ケースに分類できます。
(1)4点が一直線上に存在。
(2)適当な3点が一直線上に存在し残りはその直線上にない。
(3)如何なる3点も一直線上になく、どんな順に結んでも凹四角形である。
(4)如何なる3点も一直線上になく、適当な順に結ぶと凸四角形である。
(1)の場合は最も離れた2点を一辺とする正方形が描けます。
(2)の場合は一直線上の3点の最もはなれた2点を一辺とする正方形(上下2個)の外部に第4の点があれば正方形を描くことができます。
(3)の場合は作図不可能です。

以下(4)の場合を検討し4点は右回りABCDの順で凸四角形とします。
正方形上に4点が存在する場合その点の状態の可能性は次の3ケースがあります。
(22) 2点ずつそれぞれー辺上にある。
(211) 2点がー辺上にある。
(1111)各辺上に少なくとも1点ある。
(22)の場合の作図方と判定
この場合 AB//CD または BC//DAでなければなりません。
この平行線をkとします。
k方向の辺をもつABCDを包絡する最小の長方形を書きます。
長い方の辺で頂点を除く辺上に点が存在しないものがあれば、その辺を平行移動して正方形を作図することができます。
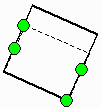
(211)の場合の作図方と判定
AB 、BC、CD、DAの4ケースを順じ試行します。
選んだ2点をP,Q 残りをR,Sとします。
PQの方向をkとします。
PQを一辺とする正方形(R,Sのある側)の内部(辺上除く)にRかSがあれば正方形を作図することは出来ません。
k方向の辺をもつABCDを包絡する最小の長方形を書きます。
長い方の辺で頂点を除く辺上に点が存在しないものがあれば、その辺を平行移動して正方形を作図することができます。

(1111)の場合の作図方と判定
この場合は いわしさん の方法で正方形を描きます。
考え方を若干解説します。
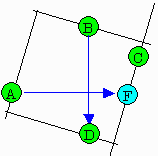
適当なk方向を考えたとき、ACのk方向の距離とBDの⊥k方向の距離が同じであれば正方形になる可能性があるわけです。
したがって、BD↓を90度左にまわしてBをAに重ねてできるDに対応の点をFとしたとき、ACのk方向の距離とAFのk方向の距離が等しければよく、kはAF↓に直交すれば良いわけです。
あるいはAF↓をk方向としても良いわけです。
以上を適用することにより、作図可能なものは作図することができます。
実際に計算すると、試した範囲では次の事実がありました。
(あ)は殆ど自明ですが(い)は不思議です。
(あ) (1)(2)(22)の場合も(211)の手法で同じ正方形を作図可能。
(い) (211)で作図可能であるが(1111)で作図不能の4点はあるが、(1111)の方法で作図可能な4点は(211)の方法で別の正方形を作図可能。
つまり、(211)の方法だけで十分となります。
これは本当でしょうか? 問題としてまとめると。
【問題】
正方形の各辺上に1点、全部で4点を配置します。
この時、何れか2点が一辺上にあり、他の2点も辺上にある正方形を作図可能である。
(1)これは真でしょうか。
(2)1辺上の2点を選ぶ簡単で効率的な方法はなにかありますか。
◆東京都の中学校3年生 もやし さんからの解答。
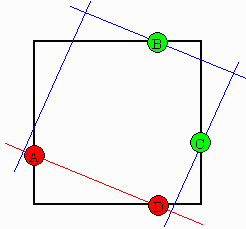
図のように、4つの点を左回りにA,B,C,Dとします。
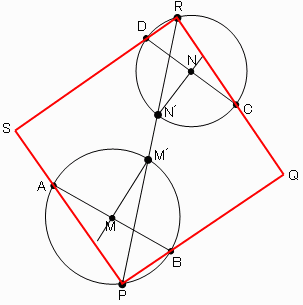
(1)線分AB,CDの垂直二等分線をかき、線分AB,CDの中点M,Nをとります。
(2)線分AB,CDを直径とする円をかき、円Mと線分ABの垂直二等分線との交点の内、線分CDに近い方をM´、円Nと線分CDの垂直二等分線との交点の内、線分ABに近い方をN´とします。
(3)直線M´N´をひき、直線M´N´と円Mとの交点の内、M´でない方をP,直線M´N´と円Nとの交点の内、N´でない方をRとします。
(4)半直線PB,RCをそれぞれひき、その交点をQ、半直線PA,RDをそれぞれひき、その交点をSとすると、四角形PQRSが求める正方形となります。
証明
AB,CDが円M,Nの直径であることから、
∠APB=∠CRD=90°
また、弧AM´=弧BM´、弧CN´=弧DN´であることから、
| ∠APM´=∠BPM´=∠CRN´=∠DRN´=90°× | 1 2 |
=45° |