 丂
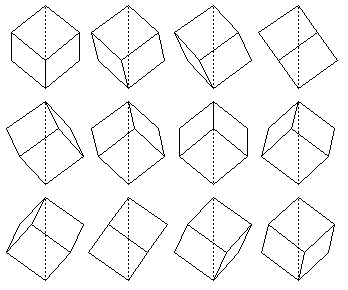
丂恾侾偼丄僒僀僐儘傪懳妏慄乮挿偝俁
 乯傪幉偵夞偟偨偲偒偺恾偱偡丅
乯傪幉偵夞偟偨偲偒偺恾偱偡丅
仧惷壀導丂儓僢僔乕偝傫偐傜偺夝摎丅
 丂
丂
恾侾偼丄僒僀僐儘傪懳妏慄乮挿偝俁 乯傪幉偵夞偟偨偲偒偺恾偱偡丅
乯傪幉偵夞偟偨偲偒偺恾偱偡丅
乮侾侽搙偒偞傒偱丄幉偵懳偟悅捈側曽岦偐傜尒偨恾乯
 丂
丂
偙傟傪廳偹傞偲丄恾俀偺傛偆偵側傝傑偡丅
敿宎嵟戝偺晹暘偺敿宎乮 乯偼丄忋侾乛俁偺墌悕偺崅偝
乯偼丄忋侾乛俁偺墌悕偺崅偝 偲丄曣慄偺挿偝乮亖僒
僀僐儘偺侾曈乯俁偲偺嶰暯曽偐傜弌傑偡丅
偲丄曣慄偺挿偝乮亖僒
僀僐儘偺侾曈乯俁偲偺嶰暯曽偐傜弌傑偡丅
拞墰偺偔傃傟偨晹暘偼丄僒僀僐儘傪偙偺柺偱愗傞偲抐柺偑丄侾曈俁 乛俀偺惓榋妏宍偵側傝傑偡偐傜丄奜愙墌偺敿宎傕摨偠偔俁
乛俀偺惓榋妏宍偵側傝傑偡偐傜丄奜愙墌偺敿宎傕摨偠偔俁 乛俀偱偡丅
乛俀偱偡丅
恾俀偺恾宍偼丄敿宎 丄崅偝
丄崅偝 偺墌悕乮俙乯偑俀偮偲丄
偺墌悕乮俙乯偑俀偮偲丄
敿宎 丄崅偝俁亄俀
丄崅偝俁亄俀 偺墌悕偐傜丄
偺墌悕偐傜丄
敿宎俁 乛俀丄崅偝俁亄俁
乛俀丄崅偝俁亄俁 乛俀偺憡帡側墌悕傪愗傝庢偭偨恾宍乮俛乯偑俀偮偐傜弌棃偰偄傑偡丅
乛俀偺憡帡側墌悕傪愗傝庢偭偨恾宍乮俛乯偑俀偮偐傜弌棃偰偄傑偡丅
丂佹崅偝傪倶偲偡傞偲丄
乮 亅俁
亅俁 乛俀乯丗
乛俀乯丗 乛俀亖
乛俀亖 丗倶
丗倶
丂傛傝丂倶亖俁亄俀
恾宍俙偺懱愊
侾乛俁亊兾亊 2亊
2亊 亖俀
亖俀 兾
兾
恾宍俛偺懱愊
傑偢敿宎 丄崅偝俁亄俀
丄崅偝俁亄俀 偺墌悕偺懱愊偼丄
偺墌悕偺懱愊偼丄
侾乛俁亊兾亊 2亊乮俁亄俀
2亊乮俁亄俀 乯
乯
亖乮俇亄係 乯兾
乯兾
師偵丄敿宎俁 乛俀丄崅偝俁亄俁
乛俀丄崅偝俁亄俁 乛俀偺墌悕偺懱愊偼
乛俀偺墌悕偺懱愊偼
侾乛俁亊兾亊(俁 乛俀)2亊乮俁亄俁
乛俀)2亊乮俁亄俁 乛俀乯
乛俀乯
亖乮俋乛俀亄俋 乛係乯兾
乛係乯兾
堷偒嶼偟偰
乮俇亄係 乯兾亅乮俋乛俀亄俋
乯兾亅乮俋乛俀亄俋 乛係乯兾
乛係乯兾
亖乮俁乛俀亄俈 乛係乯兾
乛係乯兾
慡懱愊亖俀 兾亊俀亄乮俁乛俀亄俈
兾亊俀亄乮俁乛俀亄俈 乛係乯兾亊俀
乛係乯兾亊俀
丂丂丂亖乮俁亄侾俆 乛俀乯兾
乛俀乯兾
亂弌戣幰偺悈偺棳傟偝傫偐傜偺僐儊儞僩亃
丂忋壓俁暘偺侾偺晹暘偼椙偄偺偱偡偑丄恀傫拞俁暘偺侾偼俀偮偺墌悕戜偺傛偆偵巚偭偰偍傜傟傑偡偑丄偁偺晹暘偺嬋柺偺曣慄傒偨偄偺偼捈慄偱側偔丄鉟楉側夋憸傪傛偔尒偰傕暘偐傞傛偆偵丄曻暔慄側偺偱偡丅
偩偐傜丄偳偆偟偰傕丄愊暘偺椡傪棙梡偟側偗傟偽側傜側偄偺偱偼側偄偱偟傚偆偐丠丅
仧惷壀導丂儓僢僔乕偝傫偐傜偺夝摎丅
崱擔偨傑偨傑丄夝摎偺恾俀傪尒偰偄偨傜丄乽捈慄偵側偭偰側偄偧乿偲婥偯偒丄乽傗偽偄偭両乿偲巚偄丄傆偲尒偨傜悈偺棳傟偝傫偺僐儊儞僩偑丏丏丏偔偅
偱偼丄夝摎偺傗傝側偍偟偱偡丅
 丂
丂
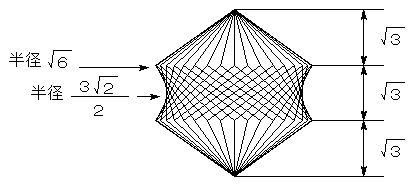
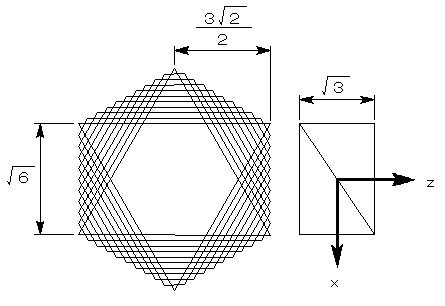
恾俁偼丄恾俀偺拞墰晹傪幉曽岦偵侾侽摍暘偟偨帪偺乮侾偮偺僒僀僐儘偺乯抐柺恾偱偡丅
恾俁偺廲曽岦偵倶幉丄夞揮幉曽岦偵倸幉傪庢傝傑偡丅
偙偺偲偒丄倶亖 倸偺娭學偑偁傝傑偡丅
倸偺娭學偑偁傝傑偡丅
夞揮懱偺敿宎倰偼丄夞揮幉偐傜丄奺抐柺乮懡偔偼榋妏宍乯偺捀揰傑偱偺嫍棧偱偡偐傜丄
倰2亖(俁 乛俀)2亄倶2亖俋乛俀亄俀倸2
乛俀)2亄倶2亖俋乛俀亄俀倸2
傛偭偰丄拞墰晹偺懱愊偼丄

慡懱愊亖俀 兾亊俀亄俆
兾亊俀亄俆 兾亖俋
兾亖俋 兾
兾
亂僐儊儞僩亃
丂崱搙偼娫堘偄側偔惓夝偩偲巚偄傑偡丅
傗偭偲偡偭偒傝偟傑偟偨丅
仧婒晫導丂悈偺棳傟偝傫偐傜偺夝摎丅
 丂 丂丂嵍偺恾偺傛偆側丄侾曈偺挿偝偑俁偺棫曽懱俷俙俛俠亅俢俤俥俧偑偁傞丅 偙偺棫曽懱傪丄捈慄俷俥偺傑傢傝偵夞揮偟偰摼傜傟傞棫懱俿偺懱愊傪媮傔傛丅 |
亙峫偊曽亜
丂夞揮懱偺懱愊傪媮傔傞栤戣偱偡偑丄堦斒偵夞揮懱傪夞揮幉偵悅捈側暯柺偱僗儔僀僗偡傞偲丄偦偺愗傝岥偼墌斅丄傑偨偼丄墌娐乮僪乕僫僢僣乯偵偟偐側傜側偄偐傜丄愗傝岥偺柺愊偼斾妑揑梕堈偵媮傔傞偙偲偑偱偒傑偡丅
偦偙偱丄偙偺栤戣偱偼丄夞揮幉俷俥忋偺揰俹傪捠傝丄俷俥偵悅捈側暯柺兛偱棫懱俷俙俛俠亅俢俤俥俧傪僗儔僀僗偟偨愗傝岥傪峫偊傑偡丅
偡傞偲丄暯柺兛偵傛傞棫曽懱偺愗傝岥偼丄嶰妏宍傑偨偼榋妏宍偲側傝傑偡丅
 丂
丂
丂丂亙恾傾亜
偙偙偱丄恾偺懳徧惈傪峫偊偰丄嶰妏宍傑偨偼榋妏宍偵偍偄偰丄揰俹偐傜丄愗傝岥偺奺捀揰傊偺嫍棧偼丄偡傋偰摍偟偄丅
 丂
丂
丂丂亙恾僀亜丂丂
偙傟傜偺恾宍傪夞揮幉偺傑傢傝偱夞揮偝偣偨偲偒墌斅傪嶌傞偑丄偦偺墌斅偺嫬奅慄傪昤偔偺偼丄夞揮偐傜嵟傕墦偄揰丄偡側傢偪丄偙傟傜偺恾宍偺捀揰偱偁傞丅亙恾僀亜
偙偺墌斅偑丄棫懱俿偺愗傝岥偱偡丅
師偵丄偙偙偱摼傜傟偨墌斅偺柺愊傪揔愗側曄悢傪梡偄偰娭悢偲偟偰昞偟傑偡丅
崱弎傋偨傛偆偵丄揰俹偐傜愗傝岥偵尰傟傞惓嶰妏宍乮傑偨偼榋妏宍乯偺奺捀揰傑偱偺嫍棧偼摍偟偄丅
備偊偵丄捀揰偺侾偮傪揰俻偲偡傞偲丄揰俻偼棫曽懱俷俙俛俠亅俢俤俥俧偵偍偄偰偼丄愜傟慄俷俙俤俥忋偵偁傞偲偟偰峫偊偰傕堦斒惈傪幐傢側偄丅
 丂
丂
丂丂亙恾僂亜
偙偺傛偆偵丄揰俹丄俻傪掕傔丄揰俹偺嵗昗傪乮倲丄倲丄倲乯丄慄暘俹俻偺挿偝傪倖(倲)偲偡傞偲丄愗傝岥偺墌斅偺柺愊俽(倲)偼丄
俽(倲)亖兾俹俻2亖兾倖(倲)2偱梌偊傜傟傞丅
丂嵟屻偵丄彫棫懱偺岤傒偺曽岦偵懳偡傞拲堄偑昁梫偱偡丅
愗傝岥偺柺愊傪梌偊傞娭悢 倖(倲)偺曄悢倲偺曄壔検嚈倲偼丄倶幉乮傑偨偼丄倷幉丄倸幉乯曽朄傊偺曄壔検偱偁傝丄彫棫懱偺岤傒偺曽朄乮偙偺応崌偼夞揮幉乯偲偼堎側傞丅
 丂
丂
亙恾僄亜
偙偺栤戣偱偼丄曄悢倲偑倶幉偺惓偺曽朄偵嚈倲憹壛偡傞偲偒丄彫棫懱偺岤傒偑幚嵺偵
夞揮幉曽朄偵偳偺偔傜偄偐傪媮傔偰傒傞偲丄![]()
憹壛偡傞偙偲偑傢偐傞丅
傛偭偰丄棫懱俿偺懱愊倁偼丄
 偱側偔偰丄
偱側偔偰丄
 偱寁嶼偟傑偡丅
埲忋偺偙偲傪棟夝偟偰丄夝摎傪偟傑偡丅
偱寁嶼偟傑偡丅
埲忋偺偙偲傪棟夝偟偰丄夝摎傪偟傑偡丅
亙夝摎亜丂揰俹(倲丄倲丄倲)傪捠傝丄儀僋僩儖俷俥亖俁(侾丄侾丄侾) 偵悅捈側暯柺兛偼丄
倶亄倷亄倸亖俁倲丒丒丒乮仏乯丂偱偁傞丅
暯柺兛偑棫懱俿偲嫟桳揰傪傕偮倲偺斖埻偼侽亝倲亝俁偱偁傝丄偙偺斖埻偱偺棫懱俿偺暯柺兛偵傛傞愗傝岥傪峫偊偰丄俿偺懱愊傪媮傔傛偆丅
棫懱俿偼丄暯柺倶亄倷亄倸亖俁乛俀偵娭偟偰懳徧偱偁傞乮俿偺丄偙偺暯柺偵傛傞愗傝岥偼恾僂傪嶲徠乯偐傜丄侽亝倲亝俁乛俀偺斖埻偵偍偗傞棫懱俿偺懱愊傪媮傔丄俀攞偡傟偽椙偄丅
暯柺兛偲愜傟慄俷俙俤偲偺岎揰俻偺嵗昗偼丄
乮侾乯揰俻偑曈俷俙忋偵偁傞偲偒乮侽亝倲亝侾偺偲偒乯丄
乮仏乯偵丄倷亖倸亖侽傪戙擖偡傞偲丄倶亖俁倲
丂丂亪俻乮俁倲丄侽丆侽乯
乮俀乯揰俻偑曈俙俤忋偵偁傞偲偒乮侾亝倲亝俁乛俀偺偲偒乯丄
乮仏乯偵丄倶亖俁丆倷亖侽傪戙擖偡傞偲丄倸亖俁乮倲亅侾乯
丂丂亪俻乮俁丄侽丆俁(倲亅侾)乯 偱偁傞丅
傛偭偰丄慄暘俹俻偺挿偝倖(倲)偼丄
|
侽亝倲亝侾偺偲偒丟 丂倖(倲)2 亖乮俁倲亅倲乯2亄倲2亄倲2 亖俇倲2
侾亝倲亝俁乛俀偺偲偒丟 |
棫懱俿傪暯柺兛偱愗偭偨愗傝岥偼墌乮撪晹傪娷傓乯偱偁傝丄偦偺柺愊俽(倲)偼丄
俽(倲)亖兾俹俻2亖兾倖(倲)2 偱偁傞偐傜丄
棫懱俿偺懱愊傪倁偲偡傞偲丄

偟偨偑偭偰丄媮傔傞棫懱俿偺懱愊倁偼丄倁亖俋 兾丒丒丒乮摎偊乯
兾丒丒丒乮摎偊乯