『細胞分裂』解答

◆東京都　小林　祐介　さんからの解答。

この手の最小問題は証明が大変なのでとりあえず思いついたものを解答しました。
もっと小さい解が存在するかもしれません。

【問題１】

半径１の球を２個詰め込むには、球を直線上に並べるしかない。

答：半径２

ここから先は試行錯誤です。

【問題２】

半径１の球を４個詰め込むには、１辺の長さが２の正四面体の頂点に球の中心を並べる方法がおそらく最小。

答：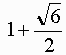

【問題３】

半径１の球を８個詰め込むには、１辺の長さが２の正六面体の頂点に球の中心を並べる方法がおそらく最小。

答え：１＋

【問題４】

半径１の球を16個詰め込むには、１辺の長さが６の正四面体において、各頂点から他の頂点へ向かって距離２の点を結ぶ平面で切った準正多面体の頂点と、準正多面体を構成する４つの正六角形の中心に球の中心を並べる方法がおそらく最小。

答：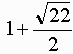

【問題５】

平面における詰め込み問題でさえ難易度が恐ろしく高いと思うのですが。
（最小の証明ができない）
問題５は解けるのでしょうか？

解けるとしたら化学でいうところの面心立方格子や六方最密構造がからんでくる気がしますが。

◆富山県　N.C　さんからの解答。

【問題３】

半径１の小球８個を、１辺の長さが２の正六面体の各頂点に中心が来るように並べる。

この８個を上の段４個と下の段４個に分け、上の段の４個（正方形の形に並んでいる）を
真上から見て４５°ひねる。
（２×２×２のルービックキューブをひねるように？）

こうすると、上の段４個と下の段４個の間には隙間ができる。
そこで隙間がなくなるまで，上の段４個と下の段４個の間隔をせばめる。
すると８個の小球は、上面と下面が正方形で側面が正三角形８個からなる立体の頂点の位置に並ぶ。

  *-----*
  |     |    展開図
  |     |
  *-----*-----*-----*-----*
   \   / \   / \   / \   / \
    \ /   \ /   \ /   \ /   \
     *-----*-----*-----*-----*
     |     |
     |     |
     *-----*

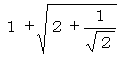
の球の中に納まることが求められる。
従って、正解はこれ以下の値になるはずである。

これはなかなかの難問であると思う。
【問題４】には手も足も出ない。
【問題３】や【問題４】の前に、
【問題２.５】「半径１の小球が６個の場合」
【問題３.５】「半径１の小球が１２個の場合」

などに取り組んで見た方が建設的かも知れません。

なお、全体の中央に小球を１個置いた場合、その周りに１２個の小球をならべて六方最密構造を作ることができ、
これらは半径３（＝１＋sqrt(４)）の球の中に納まります。

一方、辺の長さが２の正２０面体の頂点の位置に半径1の小球を１２個ならべたときの外接球の半径は、

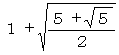
となりこれは３よりも小さな値です。

従って、小球の個数が全部で１２個以下の場合は、中央に球がくる配置を考える必要はありません。

東京都の小林さんの解答を見ての思いつきで書いてしまいました。 なお、東京都の小林さんの【問題４】の解答にある
半径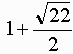

の球には、半径１の小球が少なくとも１７個つめられそうです。

◆東京都　千葉　英伸　さんからの解答。

【問題３】

図のように、正六面体の上下の４つずつを４５°ヒネるともう少し小さくできます。

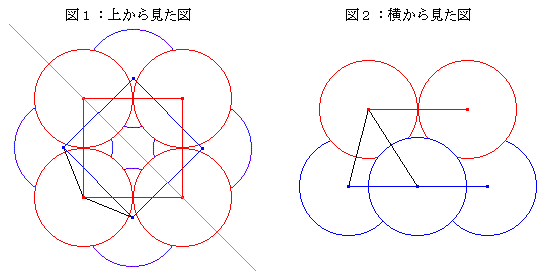
図で、赤と青の線分は、それぞれの色の上下４つずつの球の中心同士を結んだものです。

黒線は上下で隣り合う球の中心を結んだものなので、長さは２。

つまり、黒線２本と青線１本でつくられる、ちょっと斜めの三角形は正三角形です。

赤線と青線の間の高さを計算すると、

さて、図１を緑の線で垂直に切った断面を考えてみます。

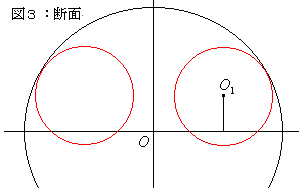
８つの小球が詰め込まれている大きな球の中心を原点にとると、
赤い小球の中心Ｏ₁ の座標は、

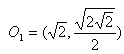
大きな球の半径をRとすると、２つの円の方程式が導かれます。

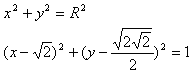この２つの円は接しているので、重解をもつ場合のRを求めればよい。
がんばって計算すると、

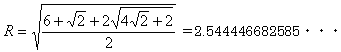
ただし、これが最小であるという保証はありません。

◆富山県　N.C　さんからの解答。

【問題４】

１６個の小球のうち、1個を中央（原点Ｏ）に配置し、
残り１５個を３個ずつ次の５階層に分けて配置します。

＃　空間座標で表記します。
でもこのデータを見て配置を頭の中で想像するのは困難ですね。

・第１階層

Ａ1（2.24cos( 58°)cos( 10°)，2.24cos( 58°)sin( 10°)，2.24sin( 58°)）
Ａ2（2.24cos( 58°)cos(130°)，2.24cos( 58°)sin(130°)，2.24sin( 58°)）
Ａ3（2.24cos( 58°)cos(250°)，2.24cos( 58°)sin(250°)，2.24sin( 58°)）

・第２階層

Ｂ1（2.24cos( 25°)cos(190°)，2.24cos( 25°)sin(190°)，2.24sin( 25°)）
Ｂ2（2.24cos( 25°)cos(310°)，2.24cos( 25°)sin(310°)，2.24sin( 25°)）
Ｂ3（2.24cos( 25°)cos( 70°)，2.24cos( 25°)sin( 70°)，2.24sin( 25°)）

・第３階層

Ｃ1（2.24cos( 0°)cos(  0°)，2.24cos( 0°)sin(  0°)，2.24sin( 0°)）
Ｃ2（2.24cos( 0°)cos(120°)，2.24cos( 0°)sin(120°)，2.24sin( 0°)）
Ｃ3（2.24cos( 0°)cos(240°)，2.24cos( 0°)sin(240°)，2.24sin( 0°)）

・第４階層

Ｄ1（2.24cos(-25°)cos(170°)，2.24cos(-25°)sin(170°)，2.24sin(-25°)）
Ｄ2（2.24cos(-25°)cos(290°)，2.24cos(-25°)sin(290°)，2.24sin(-25°)）
Ｄ3（2.24cos(-25°)cos( 50°)，2.24cos(-25°)sin( 50°)，2.24sin(-25°)）

Ｅ1（2.24cos(-58°)cos(-10°)，2.24cos(-58°)sin(-10°)，2.24sin(-58°)）
Ｅ2（2.24cos(-58°)cos(110°)，2.24cos(-58°)sin(110°)，2.24sin(-58°)）
Ｅ3（2.24cos(-58°)cos(230°)，2.24cos(-58°)sin(230°)，2.24sin(-58°)）

【小球の中心間の距離】（距離が３以上のものは省略）

・ＡiＡj＝ＥiＥj＝2.055977    (i≠jのとき)
・ＡiＢj＝ＥiＤj＝2.007181    (i≠jのとき)
・ＡiＣi＝ＥiＣi＝2.190466
・ＢiＣi-1＝ＤiＣi-1＝2.046719
・ＢiＣi+1＝ＤiＣi+1＝2.631450
・ＢiＤi＝2.020347
・ＯＡi＝ＯＢi＝ＯＣi＝ＯＤi＝ＯＥi＝2.24

なお以下のプログラム(十進BASIC)は、中央（原点Ｏ）以外の１５個の小球の中心を結んで得られる多面体を少しずつ回転させながら表示するものです。

option angle degrees
set window -3,3,-3,3

dim x(15),y(15),z(15) ! 頂点は１５個
sub vertex(R,psy,theta) ! 極座標をデカルト座標に
   let idx=idx+1
   let x(idx)=R*cos(psy)*cos(theta)
   let y(idx)=R*cos(psy)*sin(theta)
   let z(idx)=R*sin(psy)
end sub
sub vertex3(R,psy,theta) ! ３個ずつまとめて変換
   call vertex(R,psy,theta)
   call vertex(R,psy,theta+120)
   call vertex(R,psy,theta+240)
end  SUB 

let R=2.24 ! R=2.21743654373049
let t1=10 ! t1=10.766417601
let p1=25 ! p1=24.696806535
let p2=58 ! p2=58.618320649

call vertex3(R, p2,  0+t1) ! 第１階層
call vertex3(R, p1,180+t1) ! 第２階層
call vertex3(R,  0,     0) ! 第３階層
call vertex3(R,-p1,180-t1) ! 第４階層
call vertex3(R,-p2,  0-t1) ! 第５階層

dim A(39),B(39),C(39) ! 辺は３９本
sub bond(ia,ib,col) 
   let idx2=idx2+1
   let A(idx2)=ia ! ←頂点の番号
   let B(idx2)=ib  ! ←これも頂点の番号
   let C(idx2)=col ! ←これは色番号
end SUB 
sub bond2(ia,ib,col)
   call bond(ia,ib,col)
   call bond(16-ia,16-ib,col)
end SUB 

for i=1 to 3
   call bond2(i,1+mod(i,3),1) ! 第１階層同士
   call bond2(i,4+mod(i,3),2) ! 第１階層と第２階層
   call bond2(i,4+mod(i+1,3),2)
   call bond2(6+i,4+mod(i,3),4) ! 第３階層と第２階層
   call bond2(6+i,4+mod(i+1,3),6)
   call bond2(i,6+i,3) ! 第１階層と第３階層
   call bond(3+i,9+i,5) ! 第２階層と第４階層
next I 

do
   let delta=delta+1 ! 回転表示
   let eta=eta+0.03 ! 回転軸を少し傾けて表示
   let XX= cos(delta)
   let XY=-sin(delta)
   let XZ=0
   let YX= sin(delta)*sin(eta)
   let YY= cos(delta)*sin(eta)
   let YZ= cos(eta)
   clear
   for i=1 to idx2 ! 辺の表示
      set line color C(i)
      plot lines: XX*x(A(i))+XY*y(A(i))+XZ*z(A(i)),YX*x(A(i))+YY*y(A(i))+YZ*z(A(i));
      plot lines: XX*x(B(i))+XY*y(B(i))+XZ*z(B(i)),YX*x(B(i))+YY*y(B(i))+YZ*z(B(i))
   next I 
   plot points: 0,0
   for i=1 to idx ! 頂点の表示
      plot points: XX*x(i)+XY*y(i)+XZ*z(i),YX*x(i)+YY*y(i)+YZ*z(i)
   next I 
   wait delay 0.05
loop
END

◆東京都　千葉　英伸　さんからの解答。

【問題４】

１６個の場合の充填の仕方を説明します。
以下、求める大球の半径をRとし、
半径１の小球には、０〜１５までの番号を付けておきます。

まず、ｘｙ平面上に、原点Oを中心とした正七角形の頂点に並べてみます。
正七角形のうち、隣り合った２個を上下（ｚ軸方向）に少しだけずらします。
このとき、隣り合った小球は互いに接していて、
かつ、原点と中心の距離はR−１になるようにずらします。
（赤は原点に置いた球０）

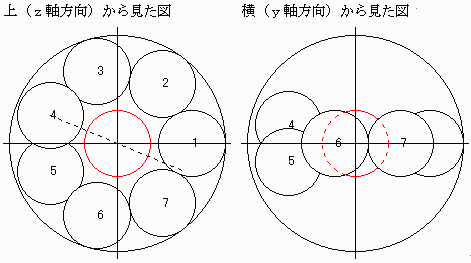
次に、球８から球１１までを正方形の形に組んで、球８と球９が球４に接するように七角形の上に置きます。

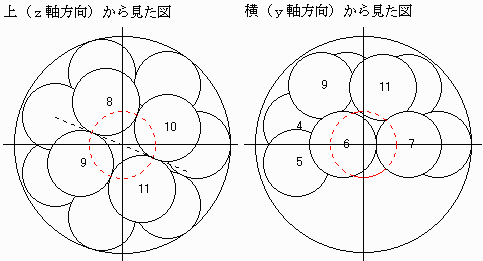
（この４つの配置は、原点と球４の中心を通り、ｚ軸に平行な平面に対称になるようにしています。
　この条件をはずすと、複雑すぎて先に進めませんでした。）

残りの球１２から球１５は上と対称になるように、下側に配置します。
この上側の４つの球が、原点と中心との距離がそれぞれR−１で、球１０と球１が接する場合の方程式を解いてRを求めます。
ただし、このままだと、球８と球３、球１１と球７がそれぞれ重なってしまいます。

そこで、原点からの距離R−１を保って、球３と球７をちょっとだけ下にずらします。
これと対称な球６と球２は同じだけ上にずらします。

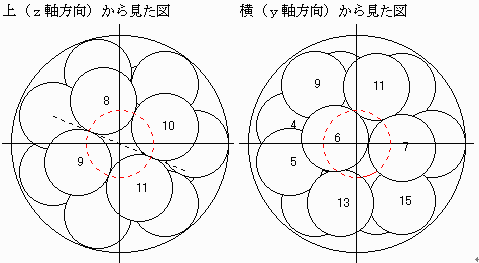
以上のように充填すると、半径Rと各球の中心の座標は以下の通りです。

R=3.2443344090097
K(0)=(0,0,0)
K(1)=(2.2443344090097,0,0)
K(2)=(1.35151046205192,1.78826013443517,0.112169969327904)
K(3)=(-0.668139459341887,2.13593645643473,-0.1685290966222)
K(4)=(-2.00923790016636,0.83659332071932,0.547824438782919)
K(5)=(-2.00923790016636,-0.83659332071932,-0.547824438782919)
K(6)=(-0.668139459341887,-2.13593645643473,0.1685290966222)
K(7)=(1.35151046205192,-1.78826013443517,-0.112169969327904)
K(8)=(-0.492388800852215,1.28823821716022,1.77060229981441)
K(9)=(-1.26115825577644,-0.558107775652477,1.77060229981441)
K(10)=(1.35320161169961,0.519783365797607,1.71339067062903)
K(11)=(0.584432156775385,-1.32656262701509,1.71339067062903)
K(12)=(-1.26115825577644,0.558107775652477,-1.77060229981441)
K(13)=(-0.492388800852215,-1.28823821716022,-1.77060229981441)
K(14)=(0.584432156775385,1.32656262701509,-1.71339067062903)
K(15)=(1.35320161169961,-0.519783365797607,-1.71339067062903)

やはり、この配置が最小である保証はありません。
上下４個ずつの正方形の対称性の条件や、最後に特定の球をちょっとずらしたりしているので、もっと小さくできるような気がします。

◆出題者の ＠ＪＪＪＪＪＪ さんからのコメント。

小林　祐介　さん、N.C　さん、千葉　英伸　さん　解答有難うございます。
１６個の場合の球の配置は私の予想外の結果でした。
（中心は正四面体がきて、原点には球がこない配置を予想していました）

◆埼玉県 \aleph_0 さんからの解答。

【問題４】

N.Cさんのアイデアを拝借しました。
まず、tをX⁵−4X⁴−X³＋5X²＋X−1の根で
3＜t＜4を満たすものとし、

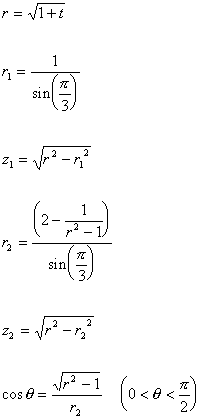
とおき、さらに

Ak (r1cos(2kπ/3＋θ), r1sin(2kπ/3＋θ),z1)
Bk (r2cos((2k＋1)π/3＋θ), r2sin((2k＋1)π/3＋θ),z2)
Ck (r cos(2kπ/3), r sin(2kπ/3), 0)
Dk (r2cos((2k＋1)π/3−θ), r2sin((2k＋1)π/3−θ),−z2)
Ek (r1cos(2kπ/3−θ), r1sin(2kπ/3−θ),−z1), (k＝0,1,2)
O (0, 0, 0)

R＝1＋r〜3.21743654371585

の球に含まれます。

　『細胞分裂』へ

　数学の部屋へもどる