『マッチ棒の一筆書き』解答
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】 18本
【問題2】 31本
【問題3】 38本
【課題】
nが偶数のとき n2+2
nが奇数のとき n2+n+1
上記式の本数の解は一般に、下図のように渦巻状にマッチを置いてゆけば得られる。
よって問題は課題解答が最大値であることを証明することである。
| 偶数 |
奇数 |
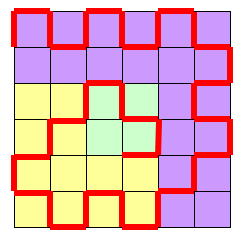 |
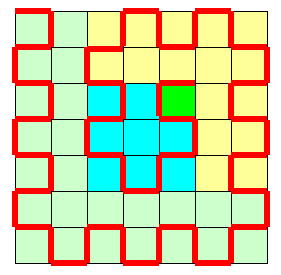 |
<偶数>
マッチは同方向に2本連続で置くことができないので、
従って、最大でn2+n本まで置ける可能性があるところまで絞られる。
さて、横2段ずつ端から切り出して考える。(下図)
このときn2+nを最大限実現するには、2段を端から切り出しているので、縦2本の位置のどちらかはマッチを置かなければならない。
即ち、中央の1列の交点は総て縦置きのマッチの頭が存在する。
ところがnは偶数なのでその頭数は奇数であり、全部を横置きのマッチで連結できない。
即ち、縦置きマッチをn+1本置くことができるのは、一筆書きの端点があるときだけである。
これは各々の2段ごとに独立に言えることである。
同様に、縦2段ずつ切り出した横置きの場合の各2段に関しても言える。
よって最大マッチの数は、
n(2段あたりの縦(or横)置きマッチ数)×n(縦2段横2段合計n組)+2(端点用)=n2+2である。

<奇数>
| 2本連続できないので 一列を見たとき最大 |
n+1
2 |
しか置けない。 |
従って、最大n2+2n+1まで置ける可能性がある。
しかしその置き方は一通りであって下図左の状態であり、一筆書きが成立しない。
この状態を解消するには、少なくとも縦または横の端から2列づつの組の総ての組の一方から1本減らしてずらさなければならず、
| 全部で |
n+1
2 |
本削減しなければならない(下図中央参照)。 |
さもないと、下図右のように小ループができる。
このとき、削減後の横(ないし縦)置きの本数は
n2+2n+1
2 |
− |
n+1
2 |
= | n2+n
2 |
であるが、 |
マッチは縦横交互に置いてゆくことから、縦置きの本数は多くても横置きの本数+1である。
よって 最大 n2+n+1 本である。
| n2+2n+1 |
(n2+2n+1)−(n+1)/2 |
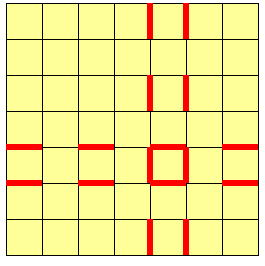
縦横両方に一組づつでも残すと |
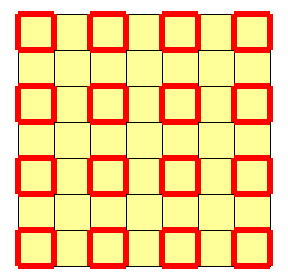 |
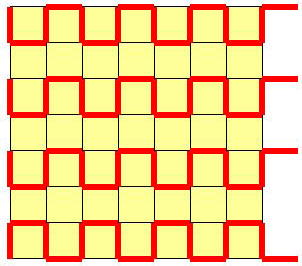 |
 |
『マッチ棒の一筆書き』へ
数学の部屋へもどる







