◆神奈川県 いわし さんからの解答。
|
BQ ――― BC | =u, |
AP ――― AQ | = v (1) |
0<u<1, 0<v<1 (2)
とおきます。
u=0またはu=1またはv=0またはv=1のとき、
すなわちPが△ABCの周上にあるとき、△QRSはつぶれてしまい面積は0ですから、除いてかまいません。
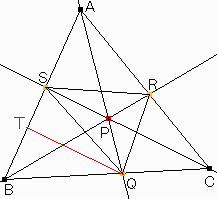
Qを通りCSに平行な直線とABの交点をTとします。

AS:ST = AP:PQ = v:(1-v),
ST:TB = CQ:QB = (1-u):u (3) ですから
|
AS ―― AB | =x = |
(1-u)v ―――――――――――――― (1-u)v+(1-u)(1-v)+ u(1-v) |
= |
(1-u)v ――――――― 1-uv |
(4) |
を得ます。同様に
|
AR ―― AC | =y = |
uv ――――――――――――― uv+u(1-v)+(1-u)(1-v) |
= |
uv ――――――― 1-(1-u)v |
(5) |
です。さて
|
△ARS ――――― △ABC |
= |
AS ――― AB |
・ |
AR ――― AC |
= xy, |
|
△BSQ ――――― △ABC |
= |
BS ――― BA |
・ |
BQ ――― BC |
= u(1-x), |
|
△CQR ――――― △ABC |
= |
CQ ――― CB |
・ |
CR ――― CA |
=(1-u)(1-y) (6) |
ですから
|
△QRS ――――― △ABC | =1-xy-u(1-x)-(1-u)(1-y) (7) |
これに(4), (5)を代入して整理すると
|
△QRS ――――― △ABC | = |
2u(1-u)v(1-v) ―――――――― 1-v+u(1-u)v2 | (8) |
が得られ、問題は(2)の範囲での(8)の最大値を求めることに帰着されます。
(8)でu(1-u) = w (9)とおくと
|
△QRS ――――― △ABC | = |
2v(1-v)・w ――――――― 1-v+(v2)・w | (10) |
(10)の右辺をf(v, w)とおきます。
vを定数と見て、fをwで微分すると
|
df ――― dw | = |
2v(1-v)2 ――――――――― (1-v+(v2)・w)2 | >0 (11) |
すなわちfはwの増加関数です。
(9)より、0<u<1の範囲でwは
u=1/2のとき最大値1/4をとりますから、このときfは最大となり、その値は
| f(v, 1/4) | = |
v(1-v)/4 ――――――――― 1-v+(v2)/4 | = |
2v(1-v) ――――――― (2-v)2 | (12) |
となります。
つまり、PをBCに平行に動かすと、vによらずQがBCの中点に一致するとき
|
△QRS ―――― △ABC | は最大となります。 |
(12)の右辺をg(v)とおきます。gをvで微分すると
|
dg ――― dv | = |
2(2-3v) ――――――― (2-v)3 | (13) |
ですから、0<v<1の範囲で
gはv=2/3のとき最大値1/4をとります。
以上より(u, v)=(1/2, 2/3)、
すなわちPが△ABCの重心に一致するとき、
|
△QRS ―――― △ABC | は最大値 |
1 ―― 4 | をとります。 |