したがって鋭角三角形：鈍角三角形の比は、１：２となる。
◆広島県 清川 育男さんからの解答。
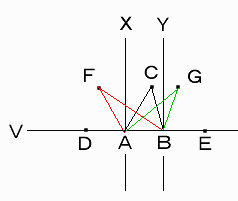
直線Ｖ上に任意に点Ｄ、点Ｅをとる。
線分ＤEの３等分点を点Ａ、点Ｂとする。
点Ａ、点Ｂを通り直線Ｖに垂直な直線をそれぞれ直線Ｘ、直線Ｙとする。
直線Ｘ、直線Ｙの間（直線Ｘ、直線Ｙ上も含む）に点Ｃをとれば、△ＣＡＢは鋭角三角形となる。
点Ｃの直線Ｘに対称な点を点Ｆとする。
△ＦＡＢは鈍角三角形となる。
点Ｃの直線Ｙに対称な点を点Ｇとする。
△ＧＡＢは鈍角三角形となる。
（直角三角形は、鋭角三角形に含めるものとする。）
このように、点Ｃに対応して点Ｆ、点Ｇがとれる。
したがって鋭角三角形：鈍角三角形の比は、１：２となる。
よって鋭角三角形になる確率は、１／（１＋２）＝１／３。
鈍角三角形になる確率は、２／（１＋２）＝２／３。
２／３－１／３＝１／３。（１／３＋２／３＝１。）
答え 鈍角三角形になる確率は鋭角三角形になる確率より１／３大きい。
以上です。
これでいいような、これではダメのような自信がありません。
無限をあつかうのはどうも。
三角形は図形の代表格ですが、今までこんな事を考えてみたことも、習った事もありません。
個数という表現ではなく、確率という表現をされているは、無限の事象だからでしょうね。
【コメント】
私もあまり自信がないのですが、出題者のAliceさん、あるいは他の方、どうでしょう。
１：１の対応ができるから、確率が同じというのは危ないと思うのですが？
この解答は正しいでしょうか。
【追加のコメント】
メールで問題点を教えてくださった方がありました。
１．△ＣＡＢは鋭角三角形とは限らない。
ＡＢを直径とする円内にＣがある場合は鈍角三角形
２．ＣとＦ、Ｇはこの方法では１：１に対応しない。
Ｆ、Ｇがずっと遠くの点のときは対応するＣは存在しない。
また１：１対応だから確率が同じというのも問題があるようです。
どなたか正解を教えてください。
◆広島県 清川 育男さんからの解答。
確率を利用して例えば円の面積を求める方法（モンテカルロ法）がありますが、逆に面積から確率を求めては、どうでしょうか。
鋭角三角形ＡＢＣを考える。
直角三角形は含めない。
この三角形二つで平行四辺形（菱形も含める）ＡＢＡ'Ｃを作る。
△ＡＢＡ'、△ＡＣＡ'は、鈍角三角形である。
また面積は鋭角三角形ＡＢＣと等しい。
したがって、線分ＡＢが確定しているとき、点Ｃと点Ａ'の取りうる確率は
（△ＡＢＣと△ＡＢＡ'の面積が等しいから）等しい。
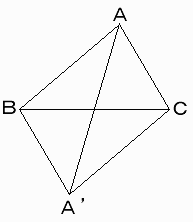
ゆえに、鋭角三角形と鈍角三角形の出来る確率は等しい。
逆は必ずしも真ならずですが、今度はこれでいいような気がします。
如何なものでしょうか。
ところで、直角三角形は、鋭角三角形と鈍角三角形のどちらに含まれるのでしょうか。
【コメント】
直角三角形はどちらにも含めないと思います。
ただ解答の正誤については私は答える能力がありませんので、ぜひどなたかメールで教えてください。
この問題は、何が同様に確からしいかを明確に定義できないといけない。
定義により答えも変わるそうです。
私自身この解答に、若干、気にいらないところもあるのですが？？？
【出題者のAliceさんからのコメント】
「△ＡＢＣと△ＡＢＡ'の面積が等しいから点Ｃと点Ａ'の取りうる確率（？）が等しい」
というところがよくわかりません。全体集合はどこなのでしょう？
せっかくの回答ですが，問題がありそうです。
何とか全体集合を有限の範囲で考えたいですね。
もちろん点は無限にあるわけですが，有限の面積で考えられると・・・
直角三角形になる確率は，同一直線上に３点が並ぶのと同じように確率ゼロでしょうね。
ちなみに，この問題のオリジナルは，私の生みの親です。誰でしたっけ？
【青木のコメント】
不思議の国のアリスのならルイス・キャロルですね。
◆神奈川県 ａｌｅｐｈさんからの解答。
【答え】
鋭角三角形となる確率：１／４
鈍角三角形となる確率：３／４
【説明】
確率(空間)をどうやって定義するかが大問題です。
３点を平面上に選んで三角形ができるとき、外接円ができます。
この円を半径１の円(単位円)に縮小して考えることにします。
問題を次のように定義します。
「単位円上に任意の３点Ａ，Ｂ，Ｃをとるとき△ＡＢＣが鋭角三角形となる確率を求めよ。
ただし点の選び方は円周上で同様に確からしい (円周上一様分布する)とする。」
点Ｃを固定し、単位円の中心をＯ、∠ＣＯＡ＝α、∠ＣＯＢ＝β、(０≦α、β＜３６０)とします。
円周上一様分布なのでα、βも一様分布になります。
(1)α≦βのとき
(α≦β≦１８０、α≦１８０≦β、１８０≦α≦βと分けて考えますが結果は同じです。)
∠Ａ＝１８０－β／２
∠Ｂ＝α／２
∠Ｃ＝(β－α)／２
なので△ＡＢＣが鋭角三角形になるのは、
１８０－β／２＜９０かつα／２＜９０かつ(β－α)／２＜９０
すなわち、
α＜１８０、β＞１８０、β＜α＋１８０
(2)α＞βのときも同様にして
α＞１８０、β＜１８０、α＜β＋１８０
(1)、(2)をαβ平面上で図示すると、
β
｜
360 ＋－＋－＋－＋－＋
｜ ／｜ ／｜
＋ ＋＊＋ ＋－＋
｜／＊＊｜／ ｜
180 ＋－＋－＋－＋－＋
｜ ／｜＊＊／｜
＋ ＋ ＋＊＋ ＋
｜／ ｜／ ｜
0 ＋－＋－＋－－－＋－－α
180 360
＊の部分が鋭角三角形となる部分である。
α、βが一様分布なので確率は面積比でもとめてよい。
したがって鋭角三角形になる確率は１／４、
鈍角三角形になる確率は１－１／４＝３／４。
他の解法としては、
１．三角形の内角をｘ，ｙ，ｚとしてｘ、ｙ、ｚがすべて９０度より小さくなる確率をもとめる方法。
２．最大辺を固定して鋭角三角形になる確率をもとめる方法
(ルイスキャロル(不思議の国のアリスの著者)はこれを答えとしています。私はこれには？？です。)
を見たことがあります。
この２つは答えが異なります。
あえて上の２つとは違う解法で解きました。
【コメント】
ますます盛り上がってきましたね。
この解答には私は感心してしまったのですが、Aliceさん、他の方、どうでしょうか。
◆新潟県 ぽぽぽさんからの解答。
方針としては、３点のうち２点を固定して、最後の１点の置き場所を考えるということです。
以上です。
私は最初からこうかな？と思っていたのですが、皆さんの解答をみていくとみんな正解の様で不思議です。
やはり、最初の全体集合をどうするかということなんでしょうか、よく分かりません。
出題者の方が用意していた解答というのが非常に興味深いです。
【コメント】
なかなか興味深い解答ですね。
「３点目のχ座標は少なくとも０～１」というのは正しいような気がするし（０～１だから鋭角三角形とはいえませんが）、
でも確率０とはとても信じられない！！
もし問題点があったら誰か教えてください。
◆神奈川県 しんいち さんからの解答。
新潟県 ぽぽぽさんからの解答ですが、
「３点のうち２点をまず最初にとってしまいます。その際その２点が（0,0),(1,0)となるように座標軸をとってしまいます。」
と仮定していますが、つまりは３点のうち２点をとるとき２点間の距離を有限と仮定しています。
一方、「３点目のｘ座標はー無限大～無限大までとる可能性がある」と、最後の１点は無限大まで考慮しています。
これでは不公平で推論が成り立たないと思います。
「３点目のｘ座標は－無限大～無限大までとる可能性があるが、実は２点目も－無限大～無限大までとる可能性があったわけであり、かならずしも最初の２点が例えば(0,0),(1,0)
となるように有限の距離を持つと決定することはできない。」
と思うのですが、いかがでしょうか？
【コメント】
なるほど、確かに問題がありそうですね。
それで確率０という結果がでたのですか。
◆神奈川県 ａｌｅｐｈ さんからの解答。
また別の答えです。
【答え】
鋭角三角形となる確率：(３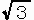
－π)／(３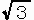＋２π)
鈍角三角形となる確率：３π／(３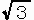＋２π)
【説明】
今度は細かいことは書きません。見てください。
ＡＢを二番目に長い辺とし固定する。
半径をＡＢとしＡ，Ｂを中心とする円を円Ａ，円Ｂと呼ぶと、点Ｃの存在範囲は円Ａの外側で円Ｂの内側 または円Ａの内側で円Ｂの外側となります。
（下の図の＋と－をあわせた領域です。)
このうち鋭角三角形となるのは－のところです。
鈍角三角形となるのは＋のところです(半円Ａ，半円Ｂ)。
｜ ｜
＊ ＊
＊ ｜－＊＊－｜ ＊
＊ ｜＊ ＊｜ ＋ ＊
＋ ｜ ｜
Ａ｜ ｜Ｂ
－－＊－－－－＊－－－－＊－－－－＊－－
｜ ｜ ＋
＋ ｜ ｜
＊ ｜＊ ＊｜ ＊
＊ ｜－＊＊－｜ ＊
＊ ＊
｜ ｜
これより面積比から、先の解を得る。【コメント】
さて、いよいよ混乱してきました。
でもこの混乱が楽しい！！
出題者のＡｌｉｃｅさん、その他の方、ぜひコメントをお願いします。
◆広島県 清川 育男さんからの解答。
モンテカルロ法による。
正方形ＡＢＣＤを有限（？）の全体集合とする。
１辺の長さをχとする。
∠ＥＢＣ＝４５度、∠ＥＣＢ＝４５度となる点Ｅを正方形ＡＢＣＤ内にとる。
△ＥＢＣは直角二等辺三角形となる。
直角二等辺三角形ＥＢＣの面積は１／４×χ2。
正方形ＡＢＣＤの面積はχ2。
正方形ＡＢＣＤ内に点Ｆをとるとき、直角二等辺三角形ＥＢＣ内にあるとき△ＦＢＣは鈍角三角形となる。
その他は鋭角三角形となる。
その他の面積はχ2－１／４×χ2＝３／４×χ2。
鋭角三角形となる面積：鈍角三角形となる面積
＝３／４×χ2：１／４×χ2
＝３：１
したがって、鋭角三角形となる確率は、３／４。
鈍角三角形となる確率は、１／４。
（３／４＋１／４＝１。）以上です。
ａｌｅｐｈさんの解答と逆になってしまいました。
どうなっているのでしょうか。
今度こそ、これでいいと自分では思っているのですが。
◆広島県 清川 育男さんからの訂正。
最初の解答のときに指摘されていた点をまた無視していました。
正方形ＡＢＣＤ、一辺がχとする。
辺ＢＣを固定して、点Ｆを取ったとき、△ＦＢＣがどうなるか、
アイデアは同じですが、直角二等辺三角形ＥＢＣが間違いで辺ＢＣを直径とする半円Ｏとしなければ、いけません。
点Ｆが、半円Ｏ内のとき△ＦＢＣは鈍角三角形、それ以外の正方形ＡＢＣＤ内のとき鋭角三角形となる。
結論は、鋭角三角形となる確率１－π／８。鈍角三角形となる確率。π／８。
（１－π／８）＋π／８＝１
以上です。
今度こそ、指摘された誤りをクリアしていると思うのですが。「辺ＢＣを固定して」とするのが、誤りかもしれませんね。
◆神奈川県 ａｌｅｐｈさんからの解答。
しんいちさんのぽぽぽさんの解答に対するご指摘は、的確なもののように思います。
最初に絶対的な長さに固定されたら相手が「無限」ですから、「不公平」な感じがします。
何とかこの「不公平さ」を解消できないものでしょうか。
そこで、絶対的な長さでなく相対的な長さで考えてみたらどうでしょう。
３辺の長さの比で考えてみます。
つまり相似な三角形(裏返しは区別)は同一視するということです。
具体的にはこういうことです。
三角形の３辺の長さをａ，ｂ，ｃとするとき、
ｘ＝ａ／(ａ＋ｂ＋ｃ)，ｙ＝ｂ／(ａ＋ｂ＋ｃ)，ｚ＝ｃ／(ａ＋ｂ＋ｃ)
とします。問題はこう言い換えられます。
「三角形の三辺の長さｘ、ｙ、ｚがｘ＋ｙ＋ｚ＝１をみたすとき、
ｘ2＋ｙ2＞ｚ2 かつ
ｙ2＋ｚ2＞ｘ2 かつ
ｚ2＋ｘ2＞ｙ2(鋭角三角形の条件)となる確率を求めよ。」
計算はかなり厄介(積分が必要)ですが、たぶん(^^;
鋭角三角形となる確率：１２ｌｎ２－８ (≒０．３１８)
鈍角三角形となる確率：９－１２ｌｎ２ (≒０．６８２)
(ｘｙ平面に正射影すると、
０＜ｘ，ｙ＜１／２ かつ ｘ＋ｙ＞１／２ の領域の中で
(ｘ－１)(ｙ－１)＝１／２，
(ｘ＋ｙ)(ｙ－１)＋１／２＝０
(ｘ＋ｙ)(ｘ－１)＋１／２＝０
に囲まれた湾曲三角形の部分が鋭角三角形となる部分)
また違う答えになりました。
ここまでいろんな解答がでてくると「正解はなんなんだぁー」という声が聞こえてきそうです。
◆神奈川県 近藤 竜生さんからの解答。
水を差すような答で申し訳ありませんが、「平面上の３点からなる三角形が鋭角三角形である」という確率は、これだけでは決まりません。
有限な領域の列を考えて、それの極限をとると答がありそうに思えますが、領域の取り方によって値が異なります。
言い換えると、なって欲しい（笑）確率を一つ決めると、その確率に収束するように領域の取り方を選ぶことができます。
「正方形内の３点の極限」、「円内の３点の極限」、「辺の長さの総和が一定」、「面積が一定」などの条件がつくと決まります。
【コメント】
私もいろいろ教えていただいて分かりましたが、絶対的な答えはないということですね。
確率をどう計算するか定義されていませんから、自分で定義しないといけないのですね。
キャロルの解答は、最長辺を固定して、無理に？有界領域を作り出しているそうです。
◆EISUKE SHIMIZU さんからの解答。
これは、昨年のアクチャリー試験に出ました。
試験では以下のように解答しました。
三角形の二つの角が決まると残る一つの角度は自動的に決まります。
二つの角のとりうる角度の組み合わせは以下の平面上で一様分布します。
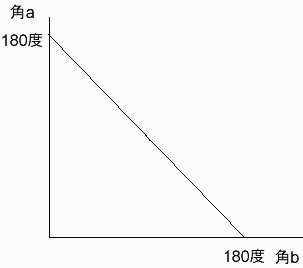
ここで、角a、角bともに90度未満になり、
かつ角a+角bが90度以上（すなわち角cが90度未満）となるケースは以下の赤い部分で示されます。
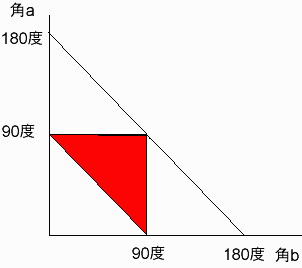
これは確率4分の１であることは明らかですね。
結局alephさんの最初の解答と同じです。
◆愛知県 数楽家Ｃｒａｎｅ（西三数学サークル）さんからのコメント。
神奈川県の近藤さんと同じです。 無限に広がる空間では「一様性」の一意な定義は無いと考えます。
無限空間中の３点を単位円上に持っていってしまうＡｌｅｐｈさんの方法は、大胆ですが私の感覚では違和感ありません。
一番納得したのは広島の清川さんの、訂正後の（π／８が出てくる方の）解答です。
◆愛知県 数楽家Ｃｒａｎｅ（西三数学サークル）さんからのコメント。
無限に広がる平面上で点を配置することの一様性を考えることは無理があります。
結論は結局「一意に定義できない。」です。
まず、一般に「分布の一様性」とは何かを考えてみます。
○ ある座標系で、ある領域Ｄが定義されているとします。
座標形の種類や次元は問いません。
このＤ内で、ある量「Ｓ」が定義されているとします。
正確には、Ｄ内の任意の点Ｐ（その座標系の意味における「点」です。）の近傍ΔＤに対してある量ΔＳが定義されているとします。
この量「Ｓ」のＤ内における総量をＳとするとき、
点Ｐの位置についての関数 ｆ(Ｐ) が定義されていて、
を満たす時、この関数ｆ(Ｐ)を、「領域ＤにおけるＳの分布密度関数」と呼びます。
この場合、分布の一様性とは、ｆ(Ｐ)が定数であることです。
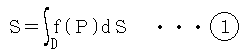
領域Ｄが無限の広がりを持つとき、Ｓが有限であるためにはｆ(Ｐ)は定数ではあり得ません。
例えばＤを数直線とするとき、ｆ(Ｐ)が正規分布関数であるような量「Ｓ」は極めて一般的に存在し、(1)を満たします。
しかし、ｆ(Ｐ)が定数であるとすると、(1)を満たすためには
ｆ(Ｐ)＝０でなくてはなりません。
つまり、無限の広がりの中で一様に分布する為には、総量が発散するか、さもなければ到る所密度が０でなくてはならないのです。
話は確率です。
「確率」という量は総量が１で有限です。
従って、無限の広がりの中での確率分布を考えると、「一様でない」か「到る所確率０」しかありえないことになります。
これは１点Ｐにおいてのみならず、有限の領域ΔＤにおいてでも同じことです。
○ 本問題の場合
無限に広がる平面上で一様な確率の下で（私にはイメージ困難ですが）３点をそれぞれ独立に選ぶわけです。
まず１点目Ａはどこに選んでも関係ありません。
２点目Ｂを選んだ途端にこの平面で「スケール」が意味を持ってきます。
つまりＡＢの距離を１としようが何としようが、ここで決めてよいわけです。
ここでスケールはともかくとして、次のように作図します。
ＡＢを直径とする円を描く。
それぞれＡ，Ｂを通りＡＢに垂直な２直線を描く。
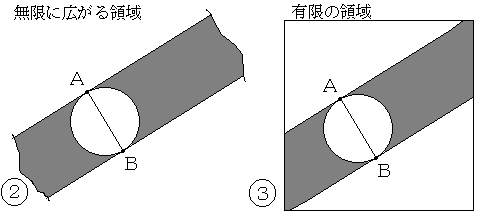
この後、第３の点Ｃを同じように任意に選ぶわけです。
点Ｃが図のグレー部分に来たときに三角形ＡＢＣは鋭角三角形となり、白い部分に来たときに鈍角三角形、円周上または２直線上に来たとき直角三角形になります。
（直線ＡＢ上に来る場合はともかくとして）
(2)は無限に広がる平面上、(3)は長方形の有限な領域内のイメージです。
(3)は面積比で確率が計算可能です。
(2)はやはり計算できません。
敢えて計算を試みるとどうなるでしょうか。
点Ｃは、無限の平面上で「一様に」ランダムに選ばなくてはなりません。
一様ならばスケールに関係ないので、どんなに遠くから眺めてもよいはずです。
どうでしょう、面積比が計算可能ですか。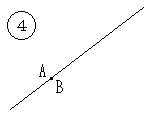
ちょっと離れただけでこの有り様です。
無限遠ではありません。
Ａ，Ｂ ２点はあくまでも別の点です。
(2)のグレー部分が、(4)では見えてこないではありませんか。
結局確率比は定義できないのです。
あえて考えようとするならば、
(4)を見る限り、０：１ である。
◆京都府 小牧愛佳 さんからの解答。
EISUKE SHIMIZU さんの解答がエレガントでいいと思います
『鋭角三角形の確率1/4』
『鈍角三角形の確率3/4』
【別解】
一般性を失うことなく一点をXY平面の原点にとります
次の点もまた一般性を失うことなくX軸上のX＞0に取ることができます
（一次変換可能のため）
ここで平面を複素数平面として捉えリーマン面を考えると
平面と球は一対一対応しますので以下リーマン面について考えます
X＜0側を選ぶと鈍角になることは容易に分かります
X＞0側については立体角=2Π（1-cosθ）より
（θはX軸上に取った位置によって0からΠの間で決まります）
鋭角になる確率は（立体角/4Π）を0からΠまでθで積分した値を
、1を0からΠまでθで積分した値、すなわちΠで割った値となりますので
（実際は半球なのでそれぞれ半分の値になりますが比なので影響なし）
（Π/2）/Π = 1/2
となります
従って鋭角三角形になる確率は以下のそれぞれの場合で
X＜0側 0
X＞0側 1/2
よって、三角形が鋭角三角形となる確率は1/4
◆東京都 妄想地区 さんからの解答。
6次元空間の点v = (x1, x2, x3, y1, y2, y3)を確率変数とします。
空間全体での一様分布は考えられないので、確率分布は回転方向について対称であり、
半径方向については確率密度関数f(r2)で表される確率分布に従うものとします。
ただし
r2 = x12 + x22 + x32 + y12 + y22 + y32
です。
vが表す三角形が鋭角三角形である条件は、vが次の集合
K = { v | (x2 - x1) (x3 - x1) + (y2 - y1) (y3 - y1) ＞ 0
(x1 - x2) (x3 - x2) + (y1 - y2) (y3 - y2) ＞ 0
(x1 - x3) (x2 - x3) + (y1 - y3) (y2 - y3) ＞ 0 }
に属することです。
以下、f(r2)は自由度6のカイ二乗分布
| f(r2) = | 1 16 | r4 exp(- |
r2 2 | ) |
こうするとvは6次元の標準正規分布N(0, I_6)に従います。
つまりx1, x2, x3, y1, y2, y3は標準正規分布N(0, 1)に独立に従います。
次に変数変換を行います。
| x1 = |
1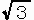 | x1' - |
1 |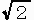
x2' + |
1 |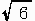
x3' |
| x2 = |
1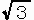 | x1' - |
2 |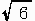
x3' |
| x3 = |
1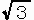 | x1' + |
1 |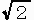
x2' + |
1 |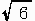
x3' |
| y1 = |
1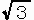 | y1' - |
1 |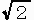
y2' + |
1 |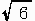
y3' |
| y2 = |
1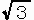 | y1' - |
2 |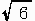
y3' |
| y3 = |
1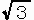 | y1' + |
1 |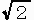
y2' + |
1 |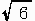
y3' |
この変換に対応する変換行列は直交行列なので、
v' = U-1 v = (x1', x2', x3', y1', y2', y3') も
標準正規分布N(0, I_6)に従います。
K' = { v' | U v' ∈ K }
= { v' | √3 (x2' x3' + y2' y3') ＜ x2'2 + y2'2
3 (x3'2 + y3'2) ＞ x2'2 + y2'2
-√3 (x2' x3' + y2' y3') ＜ x2'2 + y2'2 }
K'の右辺はx1', y1'を含まないので、x1', y1'に関する積分を先に実行することが出来ます。
残りのx2', x3', y2', y3'については具体的に積分を計算します。
x2', y2'を固定したとき、x3', y3'の積分範囲は次の図のようになります。
| I = |
1 2π |
∞ ∫ -∞ |
∞ ∫ -∞ |
exp(- |
x2'2 + y22 2 | ) J( |
√(x2'2 + y22) 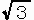| ) dx2' dy2' |
| J(s) = |
1 2π |
s ∫ -s |
∞ ∫ -∞ |
exp(- |
X2 + Y2 2 | ) dX dY- |
1 2π |
s ∫ 0 |
R exp(- |
R2 2 | ) dR |
2π ∫ 0 |
dθ |
整理して
代入して計算すると、鋭角三角形になる確率は
| I = |
∞ ∫ 0 | R exp(- |
R2 2 | )J( |
R 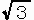| ) dR |
| J(s) = (√(2/π)) |
s ∫ 0 | exp(- |
Y2 2 | ) dY - |
s ∫ 0 | R exp(- |
R2 2 | ) dR |
代入して計算すると、鋭角三角形になる確率は
| I = |
1 ― 4 | となります。 |
(感想)
大変面白い問題でした。
エレガントな解法とは言えませんが、確率の定義は一番説得力があると自負しています。
◆東京都 建築家 さんからの解答。
この場合確率が存在しないというのは少し納得し難いと思います。
実際にそれなりに広い紙に点を3つ落としてみるとある確率で鋭角三角形と鈍角三角形に分かれるはずなので。
それが無限に広がったところで確率がそんなに変化するでしょうか・・。
混乱の大本は以下の【仮定1】に基づくものによると思われます。
【仮定1】『1点目と2点目の距離を1とした時に次の3点目が落とされる確率が全平面において一様である。』
一見正しいようですが少し納得のいかない部分もあります。
これに反する仮定を挙げてみます。
【仮定2】『2点目が3点目よりも1点目に近い確率は半々(1/2)である。』
これは多分直感的に間違いがないかと思ってます。
【仮定1】が成り立つとすれば、
1点目を原点に取った時に3点目が半径rの円の中に入る確率は０に収束するので、
(r→∞と考えてみると)
なぜか最後に取った3点目が始めの2つの点から無限遠に孤立し【仮定2】に反する結果となります。
つまり、「2点を先に決めてしまった場合最後の3点目が落とされる確率は全平面(有限に区切ろうが)において
一様ではない」ということのようです。
2点間の距離を有限としているからか単位化したからかでしょうか。
この【仮定1】を用いてない解法となるとやはり
「鋭角3角形になる確率が1/4」でよいのではと思います。
角度の和や円周上に点が乗るといった三角形に普遍な性質を用いた解法であれば間違いがないかと思われま
す。
◆宮城県 甘泉法師 さんからの解答。
平面は難しいので球面で考える。
半径１の球面がある。
単位面積あたり同じ確率で表面に点を配置する。
点Cを北極とする極座標θ,φをとる。
| 点Bがdθにある確率は、 | sinθ 2 |
dθ |
| 領域Ｍの面積 4π |
は | θ 2π | 。 |
| 球面三角形の余弦定理cosA = | cos a - cos b cos c sin b sin c |
から |
| これを満たす領域Ｎの面積 4π |
をＳ(cosθ)とする。 |
領域Ｎはθの増加とともに広がり、Ｓは０から増加。
θ<<1 ならば、関係式をa,b,cで展開して θ2≧b2+c2
| 半径 | θ 2 |
の円 4πS～ | π 4 |
*θ2 |
| θ＝ | π 2 |
で領域ＭとＮは一致し、Ｓ＝ | 1 4 |
。 |
| θ＞ | π 2 |
ならば球面三角形ABCは鈍角三角形。 |
よって球面三角形ＡＢＣが球面鋭角三角形である確率は
| 1 2 |
* |
π/2 ∫ 0 | ｛ | θ 2π |
-Ｓ(cosθ)｝sinθ dθ |
| = | 1 4π |
- | 1 2 |
* |
1 ∫ 0 | Ｓ(t)dt＜ | 1 4π |
【コメント】
Ｓの具体的式はわかりませんでした。
上の結果は球の半径によらないので、平面を半径無限大の球とみなして上の結果を適用する、という新たな考え方の提案です。
◆新潟県 white ice さんからのコメント。
皆さんの回答の中で簡単に試行できるものについて、
224回試行した場合の鈍角三角形となった確率を求めてみました。
1.と2.から、3点の取りうる領域に形があるものは確率が異なることが予想され、3.と4.では少なくとも一方には3点の取りうる領域があることが予想されます。
3.は3辺の長さを同じ領域内でランダムに選んでいるので、領域があるともいえるかもしれません。
4.はどうなのでしょう？
224回試行の修正と続きです。
問題の定義に合うのは4. だと思うのですが。