
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】
難しいですね。
x が単独素数の冪である場合に限り、N と x から単純に数える(計算量:N2のオーダー)よりは簡単に計算する方法(計算量:log(N)のオーダー)を示します。
【xが素数=Pの場合】
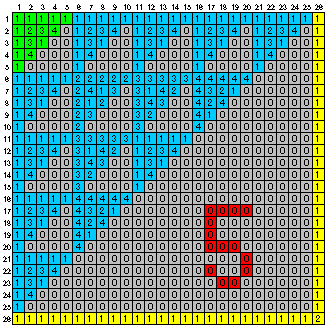
xが素数の場合を下図(x=2,3,5の場合をmod xで計算し色分け)に示す。
xの倍数ではない方に着目すると、
次元log(x(x+1)/2)./log(x)のフラクタルになっていることが分かります。
従って、Nを通常のx進法で表わし
| N= | K ∑ k=0 |
Rk*xk | であるとき |
G(N)=N2-H(K)
ここで
| H(k)= | Rk(Rk+1) 2 |
*( | x(x+1) 2 | ) | k | +(1+Rk)H(k-1) & H(-1)=0 |
証明はx=Pmの場合に含みます。


【xが単独素数の冪 x=Pmの場合】
この場合も単純ではありませんが、一応フラクタルになっています。
下図参照。
【補題1】
Pを素数とし、0≦A<Pk, 0≦B<Pk ,
0≦α<P, 0≦β<P,1≦kの整数であるとき、
| F | P | ( | Combination(A+B+(α+β)Pk, A+αPk) Combination(A+B, A) |
)=[ | A+B+(α+β)Pk Pk+1 | ] |
ここでFP (Q)はQの素因数Pの冪数である。
また[ ]はガウス記号である。
| ∵ 一般にFP(Q!)= | log(Q)/log(P) ∑ J=1 | [ | Q PJ |
] である。 |
従って、
FP((A+αPk )!)
| = | k ∑ J=1 | {[ | A PJ |
] +αP | k―J | }+ | ∑ J=1 |
[ | α PJ |
] |
| =FP(A! )+α | Pk-1 P-1 |
| 同様に、FP((B+βPk )!) =FP(B! )+β | Pk-1 P-1 |
また、
FP((A+B+(α+β)Pk )!)
| = | k ∑ J=1 | {[ | A+B PJ |
] +(α+β)P | k―J | }+ | [ | A+B Pk+1 |
+ | α+β P |
] |
| =FP((A+B)! )+(α+β) | Pk-1 P-1 |
+[ | A+B+(α+β)Pk Pk+1 |
] |
| F | P | ( | Combination(A+B+(α+β)Pk, A+αPk) Combination(A+B, A) |
) |
| =FP((A+B+(α+β)Pk )!)-FP((A+αPk )!)-FP((B+βPk )!)-FP((A+B)! )+FP(A! )+FP(B! ) |
| =[ | A+B+(α+β)Pk Pk+1 | ] |
これは、A,B<PkにおけるFP ( Combination(A+B, A))が分かっているとき、
C,D<Pk+1に対するFP ( Combination(C+D, C)) は
C+D<Pk+1 のとき FP ( Combination(A+B, A))に等しく、
C+D>Pk+1のとき FP ( Combination(A+B, A))+1であることである。
ただし C≡A、D≡B mod Pk。
【補題2】
Pを素数とし、0≦α<P, 0≦β<Pの整数であるとき。
| F | P | (Combination(α+β))=[ | α+β P |
] |
∵ 補題1でk=0 A=B=0の場合と考えればよい。
0か1である。
【本題】
よってN段のパスカルの三角形のPMの倍数の個数GP(M,N)は次のアルゴリズムで計算することができます。
<定義>
引数の数が可変の関数、
UP(K,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,])、
DP(K,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,])
を定義します。
ここで[RK-1,RK-2,RK-3,・・・ ,R1,R0,]P はK桁のP進数を表わします。
UP(K,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,]) m=0~M :
0≦A,0≦B,A+B<PK において Fp(Combination(A+B, A))=m の数
ただし、m=Mの場合は Fp(Combination(A+B, A))≧M の数
DP(K,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,]) m=0~M :
A<PK,B<PK,PK≦A+B において Fp(Combination(A+B, A))=m の数
ただし、m=Mの場合は Fp(Combination(A+B, A))≧M の数
従って GP(M,N)=UP(Y,M,[RY-1,RY-2,RY-3,・・・ ,R1,R0,])
また、特別の場合として特に Up(K,m,[P,0,0,・・・ ,0,0,])= Up(K,m)、
Dp(K,m,[P,0,0,・・・ ,0,0,])= Dp(K,m) と書きます。
<手順>
(1) N=[RY-1,RY-2,RY-3,・・・ ,R1,R0]pを求めておきます。
つまりNはY桁です。
(2) 次の漸化式で
Up(K,m)、Dp(K,m)、
K=1~Y m=0~Mを求めておきます。
Up(1,0)=P(P+1)/2
Up(1,m)=0 for M≧m>0
Dp(1,0)=0
Dp(1,1)=P(P-1)
Dp(1,m)=0 for M≧m>1
Y>K>0
Up(K+1,m)=(P(P+1)/2)*Up(K,m)+(P(P-1)/2)*Dp(K,m) for m=1~M Dp(K+1,0)=0 Dp(K+1,m,)=(P(P-1)/2)*Up(K,m-1)+(P(P+1)/2)*Dp(K,m-1) for m=1~M-1 Dp(K+1,M,)=(P(P-1)/2)*(Up(K,M)+Up(K,M-1))+(P(P+1)/2)*(Dp(K,M)+Dp(K,M-1))(3) 次の漸化式で
Up(1,0)=R0(R0+1)/2
Dp(1,0)=0
Up(1,1)=0
Dp(1,1)= R0(2P-1-R0)/2
Up(1,m)=0 for M≧m>1
Dp(1,m)=0 for M≧m>1
K+1>1
Up(K+1,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,]) = (RK(RK+1)/2)*Up(K-1,m)+(RK(RK-1)/2)*Dp(K-1,m) +(RK+1)*Up(K-1,m, [RK-2,RK-3,・・・ ,R1,R0,])+RK*Dp(K-1,m, [RK-2,RK-3,・・・ ,R1,R0,])Dp(K+1,0,[RK-1,RK-2,RK-3,・・・ ,R1,R0,])=0
Dp(K+1,m,[RK-1,RK-2,RK-3,・・・ ,R1,R0,]) = (RK(2P-1-RK)/2)*Up(K-1,m-1)+(RK(2*P+1-RK)/2)*Dp(K-1,m-1)+(P-1-RK)*Up(K-1,m-1, [RK-2,RK-3,・・・ ,R1,R0,])+(P-RK)*Dp(K-1,m-1, [RK-2,RK-3,・・・ ,R1,R0,])for m=1~M-1
Dp(K+1,M,[RK-1,RK-2,RK-3,・・・ ,R1,R0,]) = (RK(2P-1-RK)/2)*(Up(K-1,M-1)+Up(K-1,M))+(RK(2*P+1-RK)/2)*(Dp(K-1,M-1)+ Dp(K-1,M))+ (P-1-RK)*(Up(K-1,M-1, [RK-2,RK-3,・・・ ,R1,R0,])+ Up(K-1,M, [RK-2,RK-3,・・・ ,R1,R0,]))+(P-RK)*(Dp(K-1,M-1, [RK-2,RK-3,・・・ ,R1,R0,])+ Dp(K-1,M, [RK-2,RK-3,・・・ ,R1,R0,]))


ややこしいので、EXCELのマクロとしてのBASICのソースを添付しておきます。
【xが合成数の場合】
x=2×3の場合を下図に示します。
フラクタルとフラクタルの合成はカオスのようで、このアプローチではうまく行かないようです。
