仧怴妰導丂傐傐傐偝傫偐傜偺夝摎丅
僞僀儖傪揬傞偙偲偼偱偒側偄偱偟傚偆丅
偲偄偭偰愢柧偑榑棟揑偵偱偒傞栿偱偼側偄偺偱偲傝偁偊偢偙傫側傕傫偐側偀偲偄偆偙偲偱夞摎偟偰傒傑偡丅
乽弨旛乿
侾丏僞僀儖偵仜丄亊偺婰崋傪偮偗傑偡丅
![]()
俀丏壓抧偵傕偪傚偆偳巗徏柾條偵側傞傛偆偵仜丄亊傪偮偗傑偡丅
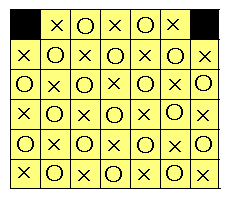
乽嶌嬈乿
壓抧偵僞僀儖傪揬傞嵺偵丄僞僀儖偲壓抧偺婰崋偑堦抳偡傞傛偆偵揬偭偰偄偒傑偡丅
仺僞僀儖偺岦偒傪曄偊傞偙偲偵傛傝丄昁偢巗徏柾條偵側傞傛偆偵偱偒傞偲巚偄傑偡
丂乮偙偙偺愢柧偑旕忢偵庛偄丅捈姶揑側傕偺側偺偱乯
乽寢壥乿
偟偐偟丄壓抧偺仜偲亊偺悢傪悢偊傞偲丄侾俋偲俀侾偵側偭偰偄傑偡丅
傕偟丄僞僀儖偱偒偭偪傝偲揬傟傞偲偟偨傜丄壓抧偺仜偲亊偺悢偼摨偠偵側偭偰偄側偗傟偽側傝傑偣傫丅
偲偄偆偙偲偼丄偒偭偪傝偲偼揬傟側偄偲偄偆偙偲偵側傝傑偡丅
乽姶憐乿
偙偺庤偺僷僘儖偭傐偄栤戣偼壗偲偐峫偊傞偙偲偑弌棃傑偡偑丄乮傕偪傠傫峫偊傞偩偗偱丄帺暘側傝偺夞摎傕側偐側偐弌偰偒傑偣傫偑乯丄偪傚偭偲愱栧悢妛偭傐偔
側傞偲慡慠傢偐傝傑偣傫丅
悢妛偼婎杮揑偵偼岲偒側偺偱偡偑丅
偙傟偐傜傕妝偟偄栤戣傪偍婅偄偟傑偡丅
亂僐儊儞僩亃
慛傗偐側愢柧偱偡偹丅
巗徏柾條偵偡傞偺偼側偐側偐婥偑偮偒偵偔偄偲巚偄傑偡丅
偦傟偱偼偝偭偦偔師偺栤戣偱偡丅
亂栤戣亃
丂壓恾偺堎側傞婰崋偺儅僗乮仜偲亊乯側傜偽偳偙偺俀枃傪庢傝彍偄偰傕丄巆偭偨晹暘傪昁偢俀亊侾偺僞僀儖偱杽傔傞偙偲偑偱偒傑偡丅
偦偺棟桼傪峫偊偰偔偩偝偄丅
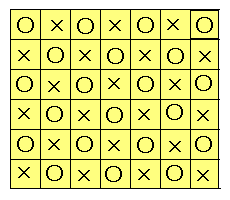
仧垽抦導丂廳塱丂戝夘 偝傫偐傜偺夝摎丅
杮棃偺栤戣偱偼丄仜偑侾俋屄丄亊偑俀侾屄偁傞丅
僞僀儖傪侾枃挘傞枅偵仜亊偺悢偑侾偮偢偮塀偝傟偰偄偔偺偱丄嵟廔揑偵偼亊偑俀屄巆傝丄偡傋偰傪杽傔傞偙偲偼偱偒側偄丅
師偵堦斒偺応崌傪徹柧偟傑偡丅
乽廲丄墶偑嬼悢丄婏悢偺挿曽宍傪巗徏柾條偵暘偗丄偦偙偐傜怓偺堘偆擟堄偺儅僗傪侾偮偢偮庢傝彍偄偰傕丄僪儈僲攙偱杽傔傜傟傞丅乿
偙偺俀儅僗傪慖傫偩偲偒丄偙偺俀儅僗傪岦偐偄崌偆俀偮偺捀揰偲偡傞挿曽宍偼廲丒墶偑嬼悢丒婏悢偺挿曽宍偱偁傞偙偲偵拲堄偡傞丅
曗戣侾丏
乽廲丄墶偑嬼悢丄婏悢偺挿曽宍偼僞僀儖偱杽傔傜傟傞丅乿
丂嬼悢偺楍偵増偭偰僞僀儖傪堦楍偵暲傋丄偦傟傪婏悢偺楍偺暘偩偗暲傋傞丅
曗戣俀丏
乽廲丄墶偑嬼悢丄婏悢偺挿曽宍偐傜岦偐偄崌偆嬿偺俀儅僗傪彍偄偰傕杽傔傜傟傞丅乿
 恾侾偱丄廲偑嬼悢丄墶偑婏悢偲偡傞偲丄曗戣侾傛傝俁偮偺挿曽宍偼杽傔傜傟傞丅
恾侾偱丄廲偑嬼悢丄墶偑婏悢偲偡傞偲丄曗戣侾傛傝俁偮偺挿曽宍偼杽傔傜傟傞丅
挿曽宍偺廲偺挿偝傪嬼悢丄墶偺挿偝傪婏悢偲偡傞丅
廲丒墶偺嬼婏偑擖傟偐傢偭偰傕摨偠傛偆側徹柧偱偁傞丅
挿曽宍偐傜俀偮偺儅僗傪庢傝彍偄偨偲偒丄偦偺俀儅僗傪俀偮偺嬿偲偡傞挿曽宍偲偦傟埲奜偺廃偺晹暘傪峫偊傞丅
乮俀儅僗偑椬愙丄傑偨偼侾捈慄忋丄傑偨偼僐偺帤偺応崌偼屻偱峫偊傞丅乯
傑偢撪懁偺挿曽宍偼曗戣俀傛傝杽傔傜傟傞丅
撪懁偺挿曽宍偺廲傪倫丄墶傪倯偲偡傞丅
 奜廃傪恾俀偺傛偆偵俉偮偺晹暘偵暘偗丄奺暥帤傑偨偼偦偺榓偺嬼婏偵傛傝応崌暘偗傪偡傞丅
奜廃傪恾俀偺傛偆偵俉偮偺晹暘偵暘偗丄奺暥帤傑偨偼偦偺榓偺嬼婏偵傛傝応崌暘偗傪偡傞丅
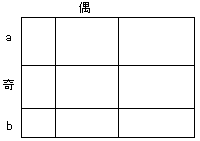 倫偑婏悢丄倯偑嬼悢偲偡傞丅
倫偑婏悢丄倯偑嬼悢偲偡傞丅
乮恾俁乯
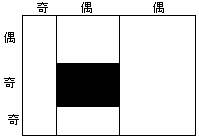
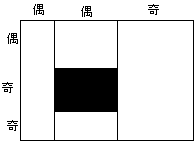
a偑嬼悢丄b偑婏悢偺偲偒丄恾俁亅侾丄恾俁亅俀偺傛偆偵暘偗丄奺挿曽宍傪杽傔傞丅
 丂
丂
恾俁亅侾
 丂
丂
恾俁亅俀
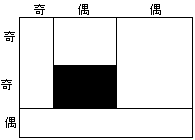
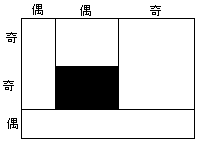
a偑婏悢丄b偑嬼悢偺偲偒丄恾俁亅俁丄恾俁亅係偺傛偆偵暘偗丄奺挿曽宍傪杽傔傞丅
 丂
丂
恾俁亅俁
 丂
丂
恾俁亅係
倫偑嬼悢丄倯偑婏悢偲偡傞丅
a偑嬼悢丄b偑嬼悢偺偲偒丄恾係亅侾丄恾係亅俀偺傛偆偵暘偗丄奺挿曽宍傪杽傔傞丅
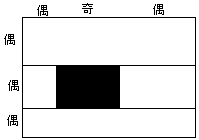 丂
丂
恾係亅侾
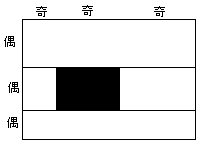 丂
丂
恾係亅俀
a偑婏悢丄b偑婏悢偺偲偒丄恾係亅俁丄恾係亅係偺傛偆偵暘偗丄奺挿曽宍傪杽傔傞丅
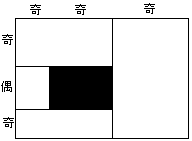 丂
丂
恾係亅俁
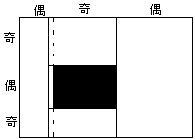 丂
丂
恾係亅係
乮恾係亅係偵拲堄丅幚慄偱暘偗傜傟偨俆偮偺椞堟傪杽傔傞丅乯
俀儅僗偑椬愙偟偰偄傞偲偒丄
偦傟偑墶偵側偭偰偄傞側傜丄恾俁亅丂偺偳傟偐偵懏偡傞丅
偦傟偑廲偵側偭偰偄傞側傜丄恾係亅丂偺偳傟偐偵懏偡傞丅
俀儅僗偑侾捈慄忋偵偁傞応崌丄偦傟傪椉抂偲偡傞挿曽宍傪峫偊傞偲丄俀儅僗偺娫偵偁傞儅僗偼嬼悢屄側偺偱杽傔傜傟傞丅
偙偺挿曽宍偑墶挿側傜恾俁亅丂偺偳傟偐丄廲挿側傜恾係亅丂偺偳傟偐偵懏偡傞丅
挿曽宍傪庢傝彍偄偨偲偒丄巆偭偨椞堟偑椫偵側傜偢僐偺帤偵側偭偰偄傞偲偒丄
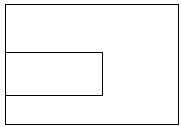 恾俆傑偨偼偦偺棤曉偟偺応崌丄
恾俆傑偨偼偦偺棤曉偟偺応崌丄
恾俆亅侾丆恾俆亅俀偺偳偪傜偐偱丄杽傔傜傟傞丅
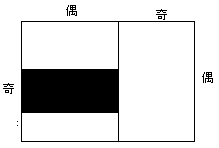 丂
丂
恾俆亅侾
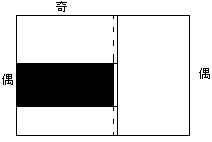 丂
丂
恾俆亅俀
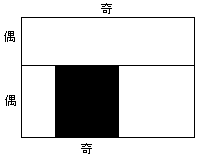
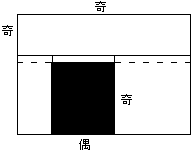
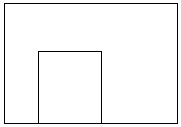 恾俇傑偨偼偦偺棤曉偟偺応崌丄
恾俇傑偨偼偦偺棤曉偟偺応崌丄
恾俇亅侾丆恾俇亅俀偺偳偪傜偐偱丄杽傔傜傟傞丅
 丂
丂
恾俇亅侾
 丂
丂
恾俇亅俀
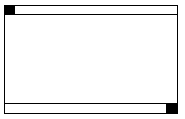
嵟屻偵丄挿曽宍傪庢傝彍偄偨偲偒丄巆偭偨椞堟偑俀偮偵暘偐傟偰偄傞偲偒傪峫偊傞丅
栤戣偵偡傋偒偼俀儅僗偑嵍塃偺楍偵偔偭偮偄偰丄忋壓偵寗娫偑偁傞応崌偱偁傞丅
乮偦偺懠偺応崌偼埲慜偲摨條偵挿曽宍傪嶌傞偲丄俀偮傑偨偼侾偮偺挿曽宍偼嬼悢丒婏悢偺挿曽宍偵側傞偺偱杽傔傜傟傞丅乯
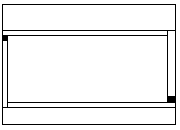
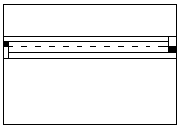
忋壓偺寗娫偺廲偑嬼悢偺応崌偼埲慜偺傛偆偵挿曽宍偵暘偗傞丅
忋壓偺寗娫偺廲偑婏悢偺応崌偼恾俈亅侾傑偨偼恾俈亅俀偺傛偆偵暘偗傟偽丄偱偒偨俈偮偺挿曽宍偼嬼悢丒婏悢偺挿曽宍偱偁傞丅
 丂
丂
恾俈亅侾
 丂
丂
恾俈亅俀
亙僐儊儞僩亜
徹柧屻敿偱偼偐側傝徣棯偟傑偟偨偑丄傎傏帺柧側偙偲偲巚偄傑偡丅
傑偨丄媡偵偔偳偄偲偙傠傕偁傞偲巚偄傑偡偑偛梕幫偔偩偝偄丅
傕偟偔偼偙傫側挿偄徹柧偱側偔丄僄儗僈儞僩側徹柧偑偁傞偐傕偟傟傑偣傫丅
偙傟偐傜帺慠偵
乮栤戣侾乯
廲丄墶偑偲傕偵嬼悢偺挿曽宍傪巗徏柾條偵暘偗丄偦偙偐傜怓偺堘偆擟堄偺儅僗傪侾偮偢偮庢傝彍偄偰傕丄僪儈僲攙偱杽傔傜傟傞偐丅
乮栤戣俀乯
廲丄墶偑偲傕偵婏悢偺挿曽宍偐傜擟堄偺侾儅僗傪庢傝彍偄偰丄僪儈僲攙偱杽傔傜傟傞偐丅
偲偄偆栤戣偑峫偊傜傟傑偡偑丄偳側偨偐壣側傜徹柧偟偰偔偩偝偄丅
栤戣侾偼摨條偵応崌暘偗偟偰徹柧偱偒傞偐傕偟傟傑偣傫丅
栤戣俀偼娙扨偱偡丅
仧搶嫗搒丂Asami 偝傫偐傜偺夝摎丅
偄傢備傞擇廳婣擺朄偲偄偆庤朄偵傛偭偰丄
| (柦戣)
彮側偔偲傕堦曈偑嬼悢側傜偽丄 丂丂丂乧乧乧仛偑恀偱偁傞偙偲傪帵偟傑偡丅 |
傑偨丄埲壓偵偍偄偰(倲,倳)偲彂偗偽丄倲峴,倳楍栚偺僞僀儖傪庢傝彍偄偨偙偲傪昞偟丄
亙倲,(倳,倳+侾)亜偱丄倲峴,倳楍,倲峴,倳+侾楍栚傪杽傔傞僪儈僲攙傪丄
亙(倲,倲+侾),倳亜偱丄倲峴,倳楍,倲+侾峴,倳楍栚傪杽傔傞僪儈僲攙傪昞偡偙偲偵偟傑偡丅
(曗戣侾)俀亊値宆偺挿曽宍偵偮偄偰仛偼惉棫偡傞
(徹柧)
(倎)丗丂(侾,倳),(俀,倳)偺偲偒
巆傝晹暘偼
亙(侾,俀),侾亜,亙(侾,俀),俀亜,乧乧,亙(侾,俀),倳-侾亜,亙(侾,俀),倳+侾亜,乧乧乧
偲杽傔傞偙偲偑壜擻
(倐)丗丂(侾,倳),(俀,倴)丂丟倳亙倴偺偲偒
(拲丗倳亜倴偺偲偒偼挿曽宍傪180搙夞揮偝偣傟偽(倐)偵婣拝)
亙(侾,俀),侾亜,亙(侾,俀),俀亜,乧乧,亙(侾,俀),倳-侾亜,
亙侾,(倳+侾,倳+俀)亜,亙侾,(倳+俁,倳+係)亜,乧乧,亙侾,(倴-侾,倴)亜,
亙俀,(倳,倳+侾)亜,亙俀,(倳+俀,倳+俁)亜,乧乧,亙俀,(倴-俀,倴-侾)亜,
亙(侾,俀),倴+侾亜,乧乧乧丂丂偲杽傔傞偙偲偑壜擻
偙傟偼倴-倳佭侽(mod俀)偩偐傜壜擻側偺偱偁傞丅
(們)丗丂(侾,倳),(侾,倴)丂丟倳亙倴偺偲偒
(拲丗(俀,倳),(俀,倴)偺偲偒偼挿曽宍傪180搙夞揮偝偣傟偽(們)偵婣拝)
亙(侾,俀),侾亜,亙(侾,俀),俀亜,乧乧,亙(侾,俀),倳-侾亜,
亙侾,(倳+侾,倳+俀)亜,亙侾,(倳+俁,倳+係)亜,乧乧,亙侾,(倴-俀,倴-侾)亜,
亙俀,(倳,倳+侾)亜,亙俀,(倳+俀,倳+俁)亜,乧乧,亙俀,(倴-侾,倴)亜,
亙(侾,俀),倴+侾亜,乧乧乧丂丂偲杽傔傞偙偲偑壜擻
偙傟偼倴-倳佭侾(mod俀)偩偐傜壜擻側偺偱偁傞丅
(曗戣徹柧廔椆)
仛偑恀偱偁傞偙偲傪帵偡偨傔偵偼丄
崱丄挿曽宍偑倫亊倯偱偁傞偲偒偺柦戣傪俼(倫,倯)偲偍偄偨偲偒偵
(嘥)丟俼(俀,俀),俼(俀,俁),俼(俀,係),俼(俀,俆),乧乧乧偑偡傋偰恀
(嘦)丟俼(俀,俀),俼(係,俀),俼(俇,俀),俼(俉,俀),乧乧乧偑偡傋偰恀
(嘨)丟俼(俀倣,値+侾),俼(俀倣+俀,値)偑恀丂佀丂俼(俀倣+俀,値+侾)偑恀
傪摫偗偽傛偄偑丄(嘥),(嘦)偼(曗戣侾)偵傛偭偰帵偝傟偰偄傞丅
偩偐傜丄崱偐傜(嘨)傪帵偦偆丅
挿曽宍俙俛俠俢丂(俙俛亖俀倣+俀,俛俠亖値+侾)偵偍偄偰
俙俤丗俤俛亖俢俧丗俧俠亖俀倣丗俀,
俙俫丗俫俢亖俛俥丗俥俠亖値丗侾偲側傞傛偆偵俤,俥,俧,俫傪偲傞丅
俤俧偲俫俥偺岎揰傪嘥偲偍偔丅
偡傞偲崱丄庢傝彍偔僞僀儖偺偆偪偺侾偮偼俙俤嘥俫偺拞偵偁傞偲偟偰傛偄丅
(佹夞揮傑偨偼愜傝曉偟偱偙傟偵婣拝偱偒傞偐傜)
傕偆侾偮偺庢傝彍偔僞僀儖偑丄俙俛俥俫傑偨偼俙俤俧俢偺拞偵偁傟偽丄
婣擺朄偺壖掕乬俼(俀倣,値+侾),俼(俀倣+俀,値)偑恀乭偵傛偭偰丄
俼(俀倣+俀,値+侾)偑恀偱偁傞偙偲傪尒傞偺偼梕堈偱偁傞丅
偟偨偑偭偰俙俤嘥俫,嘥俥俠俧偺拞偵偦傟偧傟侾偮偢偮乬庢傝彍偄偨僞僀儖乭偑偁傞偲偟偰傛偄丅
幚偼丄摨條側峫嶡偵傛偭偰丄
俙俰丗俰俢亖俛俲丗俲俠亖侾丗値,
俙俵丗俵俛亖俢俶丗俶俠亖俀丗俀倣偲側傞傛偆偵俰,俲,俵,俶傪偲偭偰
俰俲偲俵俶偺岎揰傪俷偲偡傟偽丄
俙俤嘥俫偺拞偵偁傞偲偟偨乬庢傝彍偄偨僞僀儖乭偼俙俵俷俰偺拞偵偁傞偲偟偰椙偄偺偱偁傞丅
廬偭偰埲壓偺俁偮偺応崌偵偮偄偰尒傟偽傛偄丅
(傾)丗庢傝彍偔僞僀儖偑(侾,侾),(俀倣+俀,値+侾)偺偲偒
(僀)丗庢傝彍偔僞僀儖偑(俀,侾),(俀倣+侾,値+侾)偺偲偒
(僂)丗庢傝彍偔僞僀儖偑(侾,侾),(俀倣+侾,値+侾)偺偲偒
(傾)偺偲偒偼
値佭侽(mod俀)傪堄枴偟偰偄傞偺偱
亙(俀倣+侾,俀倣),値+侾亜,乧乧,亙(俁,俀),値+侾亜,亙侾,(値,値+侾)亜,
亙(俀,俁),値亜,乧乧,亙(俀倣,俀倣+侾),値亜,亙俀倣+俀,(値,値-侾)亜,
乧乧乧,
亙俀倣+俀,(俀,侾)亜,亙(俀倣+侾,俀倣),侾亜,乧乧,亙(俁,俀),侾亜
偲偄偆晽偵偟偰杽傔傞偙偲偑壜擻偱偁傞丅
(僀)
傗偼傝値佭侽(mod俀)傪堄枴偟偰偄傞偺偱
亙侾,(侾,俀)亜,亙(俀,俁),俀亜,亙(俁,係),侾亜,亙(係,俆),俀亜,乧乧
乧乧,亙(俀倣+侾,俀倣+俀),侾亜,亙俀倣+俀,(俀,俁)亜,亙(俀倣+侾,俀倣),俁亜,
乧乧乧乧乧,亙(俁,俀),値-侾亜,亙侾,(値-侾,値)亜,亙(侾,俀),値+侾亜,
亙(俀,俁),値亜,乧乧,亙(俀倣,俀倣+侾),値亜,亙俀倣+俀,(値,値+侾)亜
偲偄偆晽偵偟偰杽傔傞偙偲偑壜擻偱偁傞丅
(僂)
値佭侾(mod俀)傪堄枴偟偰偄傞偺偱
亙俀倣+俀,(値+侾,値)亜,亙(俀倣+侾,俀倣),値亜,亙(俀倣,俀倣-侾),値+侾亜,
乧乧乧,亙(俁,俀),値亜,亙(俀,侾),値+侾亜,亙侾,(値,値-侾)亜,
亙(俀,俁),値-侾亜,乧乧乧乧乧亙俀倣+俀,(俀,侾)亜,亙(俀倣+侾,俀倣),侾亜,
乧乧乧,亙(俁,俀),侾亜
偲偄偆晽偵偟偰杽傔傞偙偲偑壜擻偱偁傞丅
埲忋偵傛偭偰 (嘨)偑帵偝傟丄
|
彮側偔偲傕堦曈偑嬼悢側傜偽丄 倫亊倯側傞挿曽宍傪巗徏柾條偵揾偭偨偲偒丄 堎怓偺僞僀儖傪侾偮偢偮庢傝彍偄偨巆傝偺儅僗傪 侾亊俀偺僪儈僲攙偱杽傔恠偔偡偙偲偑偱偒傞丅 |
仧搶嫗搒丂goya 偝傫偐傜偺夝摎丅
乽堦曈偑嬼悢偺挿曽宍偐傜堎側傞怓偺儅僗傪侾偮偢偮庢傝彍偄偰僪儈僲攙偱杽傔傜傟傞偐丠乿
偵娭偟偰丄擄偟偄夝摎偑懕偄偨偺偱娙扨乮榑棟揑側愢柧傪偟側偗傟偽丄彫妛惗偱傕懡暘擺摼偱偒傞乯側夝摎傪偟傑偡丅
垽抦導 廳塱 戝夘偝傫偐傜偺乮栤戣俀乯傊偺夝摎
廲丄墶偑偲傕偵婏悢偺挿曽宍偐傜擟堄偺侾儅僗傪庢傝彍偄偰丄僪儈僲攙偱杽傔傜傟傞偐丅
[慜採]
巗徏柾條偺揾傝暘偗偼嬿偺儅僗偺怓偑敀偲側傞敀偲崟偺巗徏柾條偲偡傞丅
仢庢傝彍偔儅僗偑崟偺帪
丂慡懱偱偼敀偺儅僗偑崟偺儅僗傛傝侾屄懡偄偺偱丄崟儅僗傪庢傝彍偔偲丄敀儅僗偑崟儅僗傛傝俀屄懡偔側傝丄偡傋偰傪杽傔傞偙偲偼偱偒側偄丅
仢庢傝彍偔儅僗偑敀偺帪
丂埲壓偺徹柧偵傛傝丄偡傋偰傪杽傔傞偙偲偑偱偒傞丅
弨旛亅侾
壓婰偺梫椞偱偡傋偰偺儅僗傪侾搙偢偮捠傞傛偆偵堦昅彂偒偡傞丅
嘆嵍壓偐傜巒傔丄嵟忋抜傑偱忋偑傞丅
嘇侾楍塃偵堏摦偟丄嵟壓抜傑偱壓偑傞丅
嘊侾楍塃偵堏摦偟丄嵟忋抜傑偱忋偑傞丅
埲壓嘇丄嘊傪孞傝曉偡丅
仸婏悢楍側偺偱廔抂偼塃忋偵側傝丄師偺傛偆側慄偵側傞丅
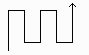
弨旛亅俀
堦昅彂偒偺慄偵増偭偰丄儅僗偵侾偐傜楢斣傪怳傞丅
偙偺寢壥丄敀儅僗偼婏悢丄崟儅僗偼嬼悢偵側傞丅乮亙曗懌亜嶲徠乯
徹柧
乮庢傝彍偔儅僗偺斣崋傪俹偲偡傞乯
俹傪庢傝彍偔偲堦昅彂偒偼 侾乣(俹亅侾) 偲 (俹亄侾)乣嵟戝抣(塃忋)丂偺俀杮偺慄偵暘偐傟傞丅
俹偼婏悢側偺偱丄俀杮偺慄偼嫟偵嬼悢屄偺儅僗傪捠傞偙偲偵側傞偐傜慄偵増偭偰僪儈僲攙傪抲偄偰偄偗偽偡傋偰偺儅僗偑杽傔傜傟傞丅
亙曗懌亜
徹柧傪尒傟偽暘偐傞傛偆偵壓婰偺忦審傪枮偨偡堦昅彂偒偱偁傟偽昅弴偵埶懚偟側偄丅
丒慄偼幬傔偵寢傋側偄(廲傑偨偼墶偵寢傇)
丒慄偼岎嵎偟側偄丅
丒慄偼挿曽宍偺奜偵弌側偄丅(儅僗偺忋傪捠傞)
椺偊偽丄偙傫側偺傕俷俲偱偡丅
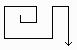
乽弨旛亅俀乿偵婰偟偨撪梕偺愢柧
嘆巗徏柾條偵廲傑偨偼墶偵慄傪堷偔偺偱敀乛崟偺儅僗傪岎屳偵捠傞丅
嘇慡懱偱偼敀儅僗偑侾屄懡偄偺偱堦昅彂偒偡傞偵偼巒抂乛廔抂偲傕敀儅僗偵側傞丅
乽俀杮偺慄偵暘偐傟傞乿偲彂偄偰偄傞偑庢傝彍偔儅僗偑巒抂傑偨偼廔抂偺帪偼乽慄偼侾杮乿偱偡偑丄偦偺慄偼嬼悢屄偺儅僗傪捠傝傑偡丅
乽堦曈偑嬼悢乣乿傕丄忋婰偺墳梡偱徹柧偱偒傑偡丅
仧搶嫗搒丂Asami 偝傫偐傜偺夝摎丅
亂僞僀儖偺俁師尦斉亃偱偡丅
斾妑揑娙扨側庤弴偱帵偡偙偲偑偱偒傑偟偨偺偱丄偛曬崘抳偟傑偡丅
| 捈曽懱傪巗徏柾條(偲屇傇偐偼抦傝傑偣傫偑)偵揾傝傑偡丅 偙傟傜偺偆偪堎側傞俀怓偺(1亊1亊1偺)僽儘僢僋傪偳偺傛偆偵庢傝彍偄偨偲偟偰傕丄俁曈偺偆偪彮側偔偲傕侾曈偑嬼悢曈側傜偽丄俀怓偺1亊1亊2偺僽儘僢僋偱杽傔恠偔偣傞丅 |
(徹柧)丗
傢偐傝傗偡偄傛偆偵丄捈曽懱偺乬偁傞乭捀揰傪尨揰偵丄嬼悢曈偑冊幉曽岦偵偔傞傛偆偵捈曽懱傪抲偔丅
(偦偺嵺丄冊幉曽岦偺曈偺挿偝傪値偲偟偰偍偔)
偦偟偰倸幉曽岦傊岦偐偭偰丄侾抜栚,俀抜栚,乧乧偲僗儔僀僗偟偰峴偒傑偡丅
(嘥)丗庢傝彍偔俀偮偺僽儘僢僋偑摨偠抜偵偁傞偲偒丅
丂偦偺抜偼俀師尦斉偱偺寢壥捠傝偵杽傔偰丄懠偺抜偵娭偟偰偼丄偦傟偧傟偺抜偵偍偄偰丄帺慠側宍偱杽傔傞偙偲偑偱偒傞丅
(嘦)丗庢傝彍偔俀偮偺僽儘僢僋偑堎側傞倲抜,倳抜(倲亙倳)偵偁傞偲偒丅
(傾)丗倲抜,倳抜偺娫偵嬼悢屄偺抜偑偁傞偲偒
丂(懄偪倳-倲佭1(mod2))
椺偊偽倲抜偵偍偄偰敀僽儘僢僋丄倳抜偵偍偄偰崟僽儘僢僋傪庢傝彍偔偲偟傛偆丅
偡傞偲丄倲抜偺係嬿偺偆偪丄(1,1)傑偨偼(1,n)惉暘偺偳偪傜偐偼崟怓偺嬿偵側偭偰偄傞(偙傟偼偳偺抜偵娭偟偰傕偄偊傞偙偲)偐傜丄椺偊偽丄(1,n)偑崟怓偺嬿偱偁傞偲偟傛偆丅
丂倲抜栚偺(1,n)偺崟怓
丂t+1抜栚偺(1,n)偺敀怓
丂t+2抜栚偺(1,n)偺崟怓
丂t+3抜栚偺(1,n)偺敀怓
丂丂乧乧乧
丂丂乧乧乧
丂u-1抜栚偺(1,n)偺崟怓
丂倳抜栚偺(1,n)偺敀怓
偙傟傜傪倸幉曽岦偵俀抜偢偮偵搉偭偰杽傔傞丅
倲抜,倳抜偺娫偵偁傞嬼悢屄偺抜偵娭偟偰偼丄巆傝晹暘傪帺慠側宍偱
(偮傑傝丄偳偺1亊1亊2僽儘僢僋傕挿偄曈偑倸幉偵暯峴偵側傞傛偆偵偟偰暲楍偝偣傞姶偠偱暲傋傞両)
杽傔傞偙偲偑偱偒丄倲,倳椉抜偵娭偟偰偼俀師尦斉偱偺寢壥捠傝偵杽傔傞丅
(僀)丗倲抜,倳抜偺娫偵婏悢屄偺抜偑偁傞偲偒
丂(懄偪倳-倲佭0(mod2))
椺偊偽倲抜偵偍偄偰敀僽儘僢僋丄倳抜偵偍偄偰崟僽儘僢僋傪庢傝彍偔偲偟傛偆丅
偦偟偰(傾)偲摨條偵丄椺偊偽倲抜偺(1,n)偑崟怓偺嬿偱偁傞偲偟傛偆丅
丂{倲抜栚偺(1,n)偺崟丂,t+1抜栚偺(1,n)偺敀}
丂{t+1抜栚偺(1,1)偺崟丂,t+2抜栚偺(1,1)偺敀}
丂丂乧乧乧
丂{u-2抜栚偺(1,n)偺崟丂,u-1抜栚偺(1,n)偺敀}
丂{u-1抜栚偺(1,1)偺崟丂,倳抜栚偺(1,1)偺敀}
偙偺傛偆偵偟偰杽傔丄倲抜栚偐傜倳抜栚傑偱偵偐偗偰丄奺抜偵偍偄偰偦傟偧傟俀師尦斉偱偺寢壥捠傝偵杽傔傞丅