◆海外の大学生 Hirasawa Yasutakaさんからの解答。
(University of North Carolina at Chapel Hill)
X = 30 degree:
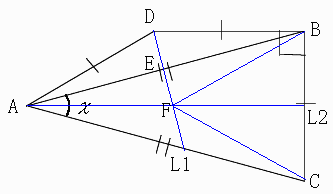
Draw a line L1 from D so that L1 is perpendicular to AB.
Call an intercept of L1 and AB as Point E.
Draw a line L2 from A so that L2 is perpendicular to BC.
Call an intercept of L2 and L1 as Point F.
Considering that triangle ACB is isosceles, we get angles CAF = BAF ( = EAF).
Triangles AFB and AFC are congruent. Thus, BF = CF.
The triangle ABD is isosceles, thus AE = EB.
This implies triangle AFB is isosceles.
Thus, AF = FB, and angles FAE = FBE.
L2 and DB are paralell ( both have right ange to BC.), thus angles FAE = EBD.
Thus, angles FBE = EBD.
This implies triangle DBF is isosceles.
Thus, DB = BF.
Summarizing these, we have got DB = BF = CF.
But DB = BC by the assumption.
Thus, triangle FCB is equilateral.
Thus, it is easy to see angle FBE = 15.
Now, X is equal to two times angle FAE.
But FAE = FBE = 15. Thus X = 30.
There must be much easier way to find the answer.
Can someone tell me how?
<青木訳>信用しないでくださいね。(^_^;
∠Xは30度
点Dから、ABに垂直に直線L1をひく。
L1とABとの交点をEとする。
点Aから、BCに垂直に直線L2をひく。
L2とL1との交点をFとする。
△ACBは二等辺三角形だから、∠CAF=∠BAF(=∠EAF)
△AFBと△AFCは合同だから、BF=CF
△ABDは二等辺三角形だから、AE=EB
したがって△AFBは二等辺三角形
したがってAF=FB、∠FAE=∠FBE
L2とDBは平行(どちらもBCと直角に交わる)なので、
∠FAE=∠EBD
したがって∠FBE=∠EBD
このことにより△DBFは二等辺三角形
したがってDB=BF
これらを総合すると、DB=BF=CFとなる
一方、仮定よりDB=BC
したがって△FCBは正三角形になる。
∠FBEは15度と容易にわかる。
∠Xは∠FAEの2倍に等しいが、∠FAE=∠FBE=15度なので
∠Xは30度。

答えを出す、もっと簡単な方法があるに違いない。
だれかおしえてくれないかなぁ
【コメント】
みごと30゜で正解です。
なるほど、こんな補助線のひき方があったのですね。
もし別な方法を考えた方がおいでましたら、ぜひメールを送ってくださいね。
◆Takaaki Yosiduさんからの解答。
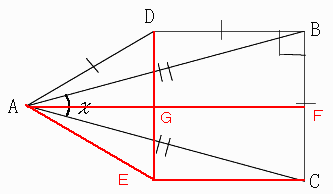
【コメント】
なるほど、この方法は簡単ですね。
△ADEが正三角形だから、∠DAE=60度。
△DABで∠ADB=∠ADE+∠BDG=60+90=150度だから
∠DAB=(180−150)/2=15度
同様に∠EAC=15度だから
∠Xは60−15×2で30度。
これはなかなかの解答だと思います。
◆岐阜県の中学校3年生 和 さんからの解答。
辺BCに平行で同じ長さの補助線を1本引く
次に点Aと点Cとその線を結び交点をEとする
三角形ADEは三辺が全て等しいので正三角形といえる
よって角ADBは60度+90度という事になり150度となる三角形ADBはADとDBの長さが等しいので二等辺三角形であり
角DAB=角DBA=15度となる
角ABC=90度−15度=75度となり三角形ABCはABとACの長さが等しいので二等辺三角形といえる
角ABC=角ACB=75度となる
よって角X=180度−75度−75度となり
角X=30度といえる
◆岐阜県の中学校3年生 なっち。 さんからの解答。
∠Aを2等分する直線Lをひく。
∠Dを2等分する直線をひき、直線Lとの交点をEとする。
点Eと点Bを結ぶ。
このとき、三角形ADBと三角形AEBは合同である。
次に、点Eと点Cを結ぶ。
このとき、三角形EBCは正三角形である。
このことから、∠DBC-∠EBC=30°となり、∠DBEは30°であることがわかる。
∠DBAと∠EBAは等しいので、∠EBAは15°となる。
三角形AEBは二等辺三角形なことから、∠EABは15°である。
∠EABと∠EACは等しいので、∠Xは30°であることがわかる。
∠X=30°
◆和歌山県 たまはち さんからの解答。
「まず、辺BCに平行で点Dを通る直線」と「辺BDに平行で点Cを通る直線」を引く。
それら2直線の交点をEとすると、□DBCEは正方形となるため、
DB=BC=CE=ED、∠ADB=∠DBC=∠BCE=∠CED=90°である。
次に点Eと点Aを結ぶ。
∠ABC=∠ACB(∵△ABCは二等辺三角形)であることから、
△ADBと△AECは合同となる。
(∵辺DB=辺EC、辺AB=辺AC、
∠DBA=「90°−∠ABC」=「90°−∠ACB」=∠ACE)
よって辺AD=辺AE=辺DEであるから、△ADEは正三角形。
よって∠ADE=∠AED=∠EAD=60°。
よって∠ADB=∠AEC=150°となり、
△ADBと△AECは二等辺三角形であることから、
∠DAB=∠DBA=∠EAC=∠ECA=15°。
よって、X=60°−(15°×2)=30°。
◆東京都 甘泉法師 さんからの解答。
点Dと、辺ABに対して対称な点Eをとると△EBCは正三角形。
四角形ABECにおいて
∠BEC=60°=∠BAC+∠ACE+∠ABE=2x
よってx=30°
◆山梨県 Footmark さんからの解答。
以下、青い補助線を引いた下図を参照してください。
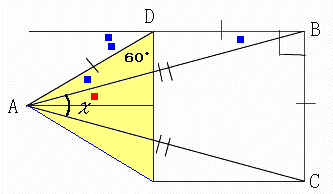
薄黄色の部分は明らかに正三角形ゆえ、■■ は30°です。
これは、■ の2倍でもあります。
一方、求める角度は ■ の2倍です。
ところが、互いに錯角のため、■=■ です。
よって、求める角度は ■■ と等しく30°です。